目录
一、合并排序相关题
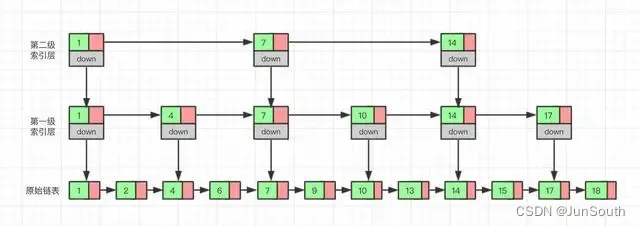
1、合并排序
2、逆序对
二、快速排序相关题
1、快速排序
目录
一、合并排序相关题
1、合并排序
2、逆序对
二、快速排序相关题
1、快速排序
2、中位数选取
三、循环赛日程表
一、合并排序相关题
1、合并排序

合并排序的原理:
(1)如果左值等于右值,返回左值对应的数组值
(2)取mid=(left+right)/2,对左侧部分合并排序,右侧部分合并排序
(3)对左排和右排进行合并排序,由于进入总合并排序中,不一定是左排和右排你一个我一个或者左排全部小于右排的原理。所以遵循几个原则:两者都没读到末尾时,数组值较小的先进总排,若有一者读到末尾,那么另一者将所有的值按顺序进入总排。
合并排序代码:
//合并排序
public class mergesort {
public static void main(String[] args)
{
int[] nums=new int[]{9,8,5,2,4,3,1,6};
int[] nums_sort=MergeSort(nums,0,nums.length-1);
for(int i:nums_sort)
{ System.out.print(i);
System.out.print(" ");
}
}
public static int [] MergeSort(int a[],int left,int right)
{
if(left==right)
return new int[]{a[left]};
int mid=(left+right)/2;
int leftarr[]=MergeSort(a,left,mid); //左侧合并排序
int rightarr[]=MergeSort(a, mid+1,right); //右侧合并排序
int newarr[]=new int[leftarr.length+rightarr.length]; //左排与右排合并
int m=0;int i=0;int j=0;
while(i<leftarr.length&&j<rightarr.length) //在两个哨兵分别没有走完左排和右排时,选择较小的先进入newarr
newarr[m++]=leftarr[i]<rightarr[j]?leftarr[i++]:rightarr[j++];
while(i<leftarr.length) //如果右排哨兵到末尾,那么左排的剩余部分加入newarr
newarr[m++]=leftarr[i++];
while(j<rightarr.length) //如果左排哨兵到末尾,那么右排的剩余部分加入newarr
newarr[m++]=rightarr[j++];
return newarr;
}
}2、逆序对
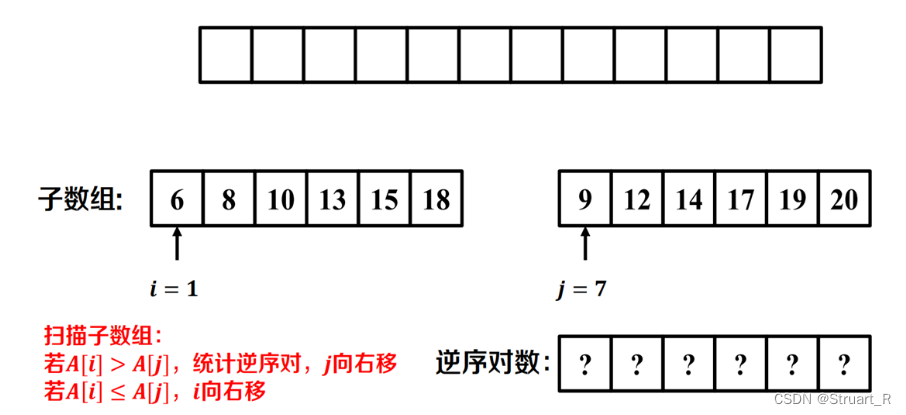
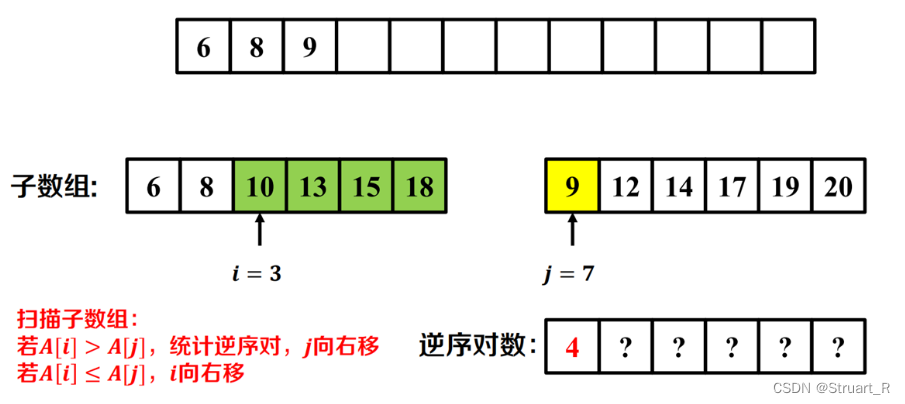
逆序对就是数组中前面的一个数大于后面的一个数,这两个数组成的关系就是逆序对。比如{4,2,3,1}中{4,2},{4,3},{4,1},{2,1},{3,1}都是逆序对。如果使用暴力枚举方法就是的复杂度,我们可以使用归并排序法降低复杂度到
。
利用归并排序,每次以左侧排序数组为基准。
(1)若左哨兵小于右哨兵,则左哨兵加1,继续判定(1)
(2)若左哨兵大于右哨兵,逆序对加mid-左哨兵索引+1,右哨兵加1,返回(1)。
(3)若右哨兵到末尾则算法停止。
逆序对代码:
public class 逆序对 {
public static void main(String[] args)
{
int[] nums=new int[]{9,8,5,2,4,3,1,6};
int nums_sort=MergeSort(nums,0,nums.length-1);
System.out.println(nums_sort);
}
public static int MergeSort(int a[], int left, int right)
{
if (left >= right)
return 0;
int mid = (left + right) / 2;
int leftans = MergeSort(a, left, mid);
int rightans = MergeSort(a, mid + 1, right);
int p = left; int q = mid + 1; int count = 0;
int[] temp = new int[right - left + 1]; int index = 0;
while (p <= mid && q <= right) {
if (a[p] > a[q]) {
count += mid - p + 1;
temp[index++] = a[q++];
} else {
temp[index++] = a[p++];
}
}
while (p <= mid)
temp[index++] = a[p++];
while (q <= right)
temp[index++] = a[q++];
for (int i = 0; i < index; i++)
a[left + i] = temp[i];
return count + leftans + rightans;
}
}
二、快速排序相关题
1、快速排序
快速排序复杂度为,具体原理请参见下面博客,写的很好。
另外如果想从降低到O(n)的话,就需要随机划分法,随机选择一个基准点,而不是永远用第一个。
快速排序有两种做法,一种是两个哨兵移动,另一种是使用基准元素遍历整个数组分割为两个部分。
快速排序(java实现)_快速排序java-CSDN博客
快速排序代码:
import java.util.Scanner;
public class QuickSort {
public static void main(String[] args){
int []arr=new int[999];int j =0;
String input=new Scanner(System.in).nextLine();
String[] numbers=input.split("\\s+");
for(String number : numbers)
{
arr[j++]=Integer.parseInt(number);
}
quickSort(arr, 0, j-1);
for (int i = 0; i < j; i++) {
System.out.print(arr[i]);
System.out.print(" ");
}
}
public static void quickSort(int[] arr,int low,int high){
int i=low; int j=high; int temp,t;
if(low>high){
return;
}
//temp就是基准位
temp = arr[low];
while (i<j) {
while (temp<=arr[j--]&&i<j) ; //右哨兵减一
while (temp>=arr[i++]&&i<j) ; //左哨兵加一
if (i<j) { //交换
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
arr[low] = arr[i]; //将基准为与i和j相等位置的数字交换
arr[i] = temp;
quickSort(arr, low, j-1); //递归调用左半数组
quickSort(arr, j+1, high); //递归调用右半数组
}
}2、中位数选取
依赖于快速排序进行中位数选取。
(1)确定数组长度的奇偶性,确定中位数的位置,奇数直接调select函数找第mid小的元素,偶数则返回第mid和mid-1的平均值。
(2)select函数根据快速排序思想,调用partition函数将数组分为两部分,并找到第k个小的元素。
(3)partition函数就是一个快速排序对特定位置的数组进行快排。
public class MedianFinder {
public static void main(String[] args){
int num[]={1,2,3,4,5,6};
double med=medianFinder(num);
System.out.println(med);
}
//寻找数组中的中位数
public static double medianFinder(int[] num){
int mid;
int len=num.length;
double med;
if(len%2==0){
mid=len/2;
med=(select(num,mid)+select(num,mid-1))/2.0;
}
else{
mid=(len-1)/2;
med=(double)select(num,mid);
}
return med;
}
//找到第k个小的元素
public static int select(int[] num,int k){
int low=0;
int high=num.length-1;
int j=0;
int val=0;
while(low<high){
j=partition(num,low,high);
if(j==k){
val=num[j];
break;
}else if(j>k){
high=j-1;
}else{
low=j+1;
}
}
return val;
}
//快速排序
public static int partition(int[] num,int low,int high){
int i=low;
int j=high;
int temp=num[i];
while(i<j){
while(i<j && temp<=num[j--]);
if(i<j)
num[i++]=num[j];
while(i<j && temp>=num[i++]);
if(i<j)
num[j--]=num[i];
}
num[i]=temp;
return i;
} 快速排序的复杂度是依据数组的对称性,如果每次选择pivot都是中位数,那么时间复杂度就是 ,但如果每次选的数都是一侧第一个值那么时间复杂度就会是
,所以为了保证不对称分布也可以保证相对对称的效果,那么就需要在选择pivot上更加随机。
可以通过修改partition函数让每一步选择pivot都是当前数组中的一个随机值,并调换他和左值的位置,产生一个随机划分效果。
//随机划分快速排序
public static int RandomizedPartition(int []num,int low,int high)
{
int i=new Random().nextInt(low,high);
swap(num,i,low);
return partition(num, low, high);
}
public static void swap(int []num,int i,int low)
{
int tmp=num[i];
num[i]=num[low];
num[low]=tmp;
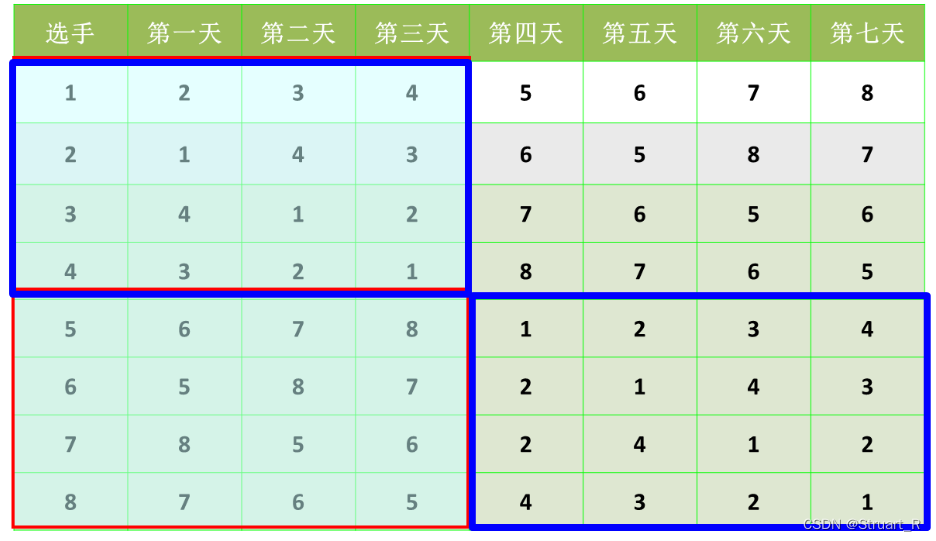
}三、循环赛日程表
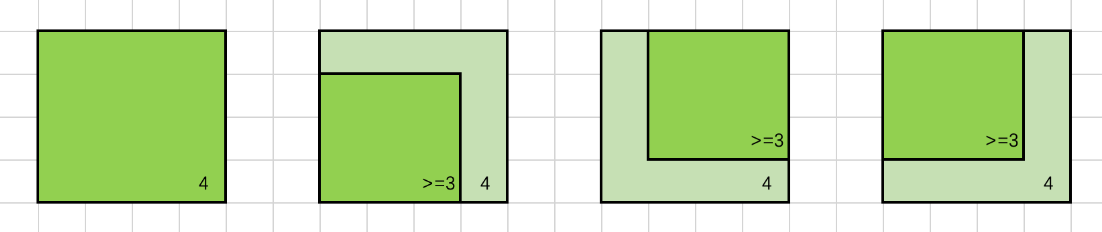
设()n个选手参加循环赛,每个选手必须与其他n-1个选手各赛一次,每个选手一天只能比赛一次,循坏赛一共n-1天。可以参照下图,能看到每一个
的格子都是对角对称的,所以可以依照这个原理进行分治。
原理:
(1)分治构造左上和右上的日程表。
(2)将左上的日程表复制到右下,右上的日程表复制到左下。
伪代码如下:
public static void table(int arr[][],int i,int j,int n)
{
if(n>1)
{
table(arr,i,j,n/2); //构造左上的日程表
table(arr,i+n/2,j,n/2); //构造右上的日程表
copy(arr,i,j,i+n/2,j+n/2,n/2); //左上的日程表复制到右下
copy(arr,i+n/2,j,i,j+n/2,n/2); //右上的日程表复制到左下
}
else
return arr[i];
}