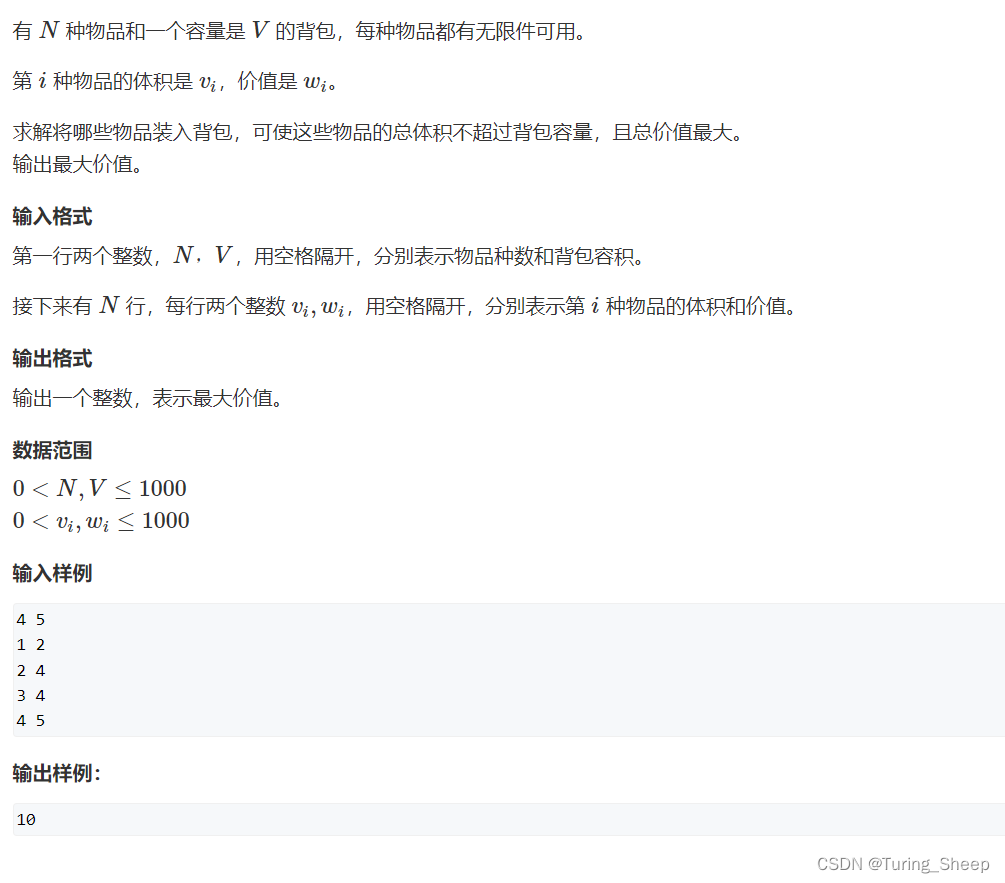
一、问题描述

二、思路分析

完全背包和01背包的区别就在于01背包中，每个物品只能选择一次，而完全背包问题中，每个物品可以选择无限次。如果大家没有看过之前01背包的讲解的话，建议大家先去看看作者之前写的01背包问题，传送门：01背包问题

那么很明显，这道题符合动态规划的三个性质：最优子结构，重叠子问题，无后效性。因此，我们可以利用动态规划的思路去解决这道题。这三个性质的分析和01背包是一样的。

那么想要利用动态规划的思路来解决这道题的话，我们需要做两件事情：

1、构建当前问题和子问题之间的关系：书写状态转移方程。
2、设计循环，记录每一个子问题的最优解。

1、状态转移方程

状态转移方程的作用是我们通过数学表达式来达到缩小问题规模。所以，我们需要用子问题来解决当前状态。而在上一节01背包问题中，我们曾经介绍过，对于背包问题中状态转移方程的书写，我们的方式是：活在当下。

我们面前要做的选择就是第i个物品，你到底是选还是不选，如果选你能选多少？

很明显，只要在容量允许的范围内，我们可以选很多个，最后我们在各种方案内选出一个最大值。

如下所示：

$$f(i,j)=max\{\begin{array}{ll}f(i-1,j)& \\ f(i-1,j-v[i]\ast 1)+w[i]\ast 1& \\ ...& \\ f(i-1,j-v[i]\ast k)+w[i]\ast k& k\ast v[i]\le j\end{array}$$

2、循环设计

循环的设计其实就是为了有条不紊地逐渐计算出规模不断增大地子问题。完全背包的循环设计和01背包的循环设计是一致的。我们逐一枚举1个物品时，各个容量下的最优解，2个物品时，各个容量下的最优解，直到n个物品下，各个容量下的最优解。

三、代码模板

1、朴素版

#include<iostream>
using namespace std;
const int N=1010;
int f[N][N],v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        scanf("%d%d",v+i,w+i);
    
    for(int i=1;i<=n;i++)//枚举物品数量
    {
        for(int j=0;j<=m;j++)//枚举容量
        {
            for(int k=0;k*v[i]<=j;k++)//书写状态方程
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k);
            }
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

2、优化版

（1）时间优化

我们发现上面的朴素版代码的嵌套了三重循环，这个时间复杂度是非常高的，我们如何降低时间复杂度呢？

同时，我们发现，我们的完全背包问题依旧是只利用$i-1$行的数据。那么我们能否像01背包一样将二维数组转化成一维数组呢？

我们先解决时间复杂度优化的问题：

我们再看一下我们刚才的状态转移方程：
$$f(i,j)=max\{\begin{array}{ll}f(i-1,j)& \\ f(i-1,j-v[i]\ast 1)+w[i]\ast 1& \\ ...& \\ f(i-1,j-v[i]\ast k)+w[i]\ast k& k\ast v[i]\le j\end{array}$$
我们刚刚的最内层循环其实就是在执行上面这个状态转移方程，最内层的循环在枚举每一种情况，然后去得出一个最大值。

那么我们就聚焦于这个过程：

假设我们当前的背包容量是$j-v[i]$,那么此时我们会去枚举该容量下的$k$种情况。最终得到一个最大值，我们将这个最大值记作：$max(j-v[i])$。此时，我们会将这个最大值记录在数组中。

接着，随着我们的第二层循环的进行，我们到了背包容量为$j$的情况，此时，我们就会开始枚举$k$种情况，去求出最大值。但是此时我们思考一下，我们是否还有必要去枚举所有的情况？

当 $k$ = 1 的时候，

我们需要比较的是 ： $f(i,j)$ 和 $f(i,j-v[i])+w[i]$，

此时假设我们得到的是下面这种结果：

$f(i,j)>f(i,j-v[i])+w[i]$

接下来，

当$k=2$的时候，

此时，我们会得到 $f(i,j-v[i]\ast 2)+w[i]\ast 2$，而这个式子可以改写为：$f(i,(j-v[i])-v[i])+w[i]+w[i]$。

那么这个式子的前半部分：$f(i,(j-v[i])-v[i])+w[i]$ 就可以看作是，我们刚才求状态$f(i,j-v[i])$的最大值时的枚举$k=1$的过程。

而我们在此之前我们已经求得了$max(j-v[i])$。所以此时一定满足：

$$f(i,(j-v[i])-v[i])+w[i]\le max(j-v[i])$$

两侧再同时加上一个$w[i]$并不影响我们的结果，即：

$$f(i,(j-v[i])-v[i])+2\ast w[i]\le max(j-v[i])+w[i]$$
我们将这个式子一般化：

我们后续过程枚举的任意一个$k$,都满足下列不等式：

$$f(i,j-k\ast v[i])+k\ast w[i]=f((i-v[i])-(k-1)\ast v[i])+(k-1)\ast w[i]+w[i]$$
$$f(i,(j-v[i])-(k-1)v[i])+(k-1)w[i]+w[i]\le max(j-v[i])+w[i]$$

因此，我们与其去枚举每个k，不如直接用之前求出的$max(j-v[i])$

于是，我们只需要进行一次下列等式的比较即可：
$$f(i,j)=max(f(i,j),max(j-v[i])+w[i])$$

那么用数组表示就是：
$$f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i])$$

上述式子表达的意思是，我们选择第$i$个物品时的最大值，但是我们是不是还有可能不选。
所以我们需要在选的情况下的最大值，和不选的情况下的值做比较。

所以，经过优化后的状态转移方程如下：
$$max=\{\begin{array}{ll}f[i][j]& j<v[i]\\ max(f[i][j],f[i][j-v[i]]+w[i])& j\ge v[i]\end{array}$$

上述的式子就可以直接代替第三层循环。

时间优化版本：

#include<iostream>
using namespace std;
const int N=1100;
int f[N][N],v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)scanf("%d%d",v+i,w+i);
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])
            f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

（2）空间优化

时间+空间优化的版本：

我们在01背包的文章中曾经介绍说，逆序进行第二层循环是为了避免重复选择。而我们的完全背包是允许进行重复选择的。如果大家没看过之前的01背包问题的文章的话，作者建议先去看一看01背包的优化，01背包传送门

因此，我们正序遍历第二层循环的情况下就可以进行空间优化，代码如下：

#include<iostream>
using namespace std;
const int N =1e3+10;
int f[N],v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",v+i,w+i);
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            if(j>=v[i])
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}