注：本次修改了添加边的一些其他情况可以采用坐标来添加边

		
void _AddEdge(size_t srci, size_t dsti, const W& w)
{
	_matrix[srci][dsti] = w;
	// 无向图
	if (Direction == false)
	{
		_matrix[dsti][srci] = w;
	}
}

void AddEdge(const V& src, const V& dst, const W& w)
{
	size_t srci = GetvertexIndex(src);
	size_t dsti = GetvertexIndex(dst);
	_AddEdge(srci, dsti, w);
}

注：本篇所用的某些未在本文中实现的函数，或不明确的类，均在上篇博客中有详细过程，因篇幅问题不再赘述。

C++--数据结构--图的相关概念及模拟实现--高阶0712_Gaze！的博客-CSDN博客

---

1. 最小生成树

在 无向图从顶点v1到顶点v2有路径，则称顶点v1与v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。

在有向图中，在每一对顶点vi和vj之间都存在从vi到vj的路径，也存在从vj到vi的路径，则此图称为强连通图。一个连通图的最小连通子图称为该图的生成树。

若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。

构造最小生成树的准则有三条：

1. 只能使用图中的边来构造最小生成树
2. 只能使用恰好n-1条边来连接图中的n个顶点
3. 选用的n-1条边不能构成回路

---

1.1 Kruskal

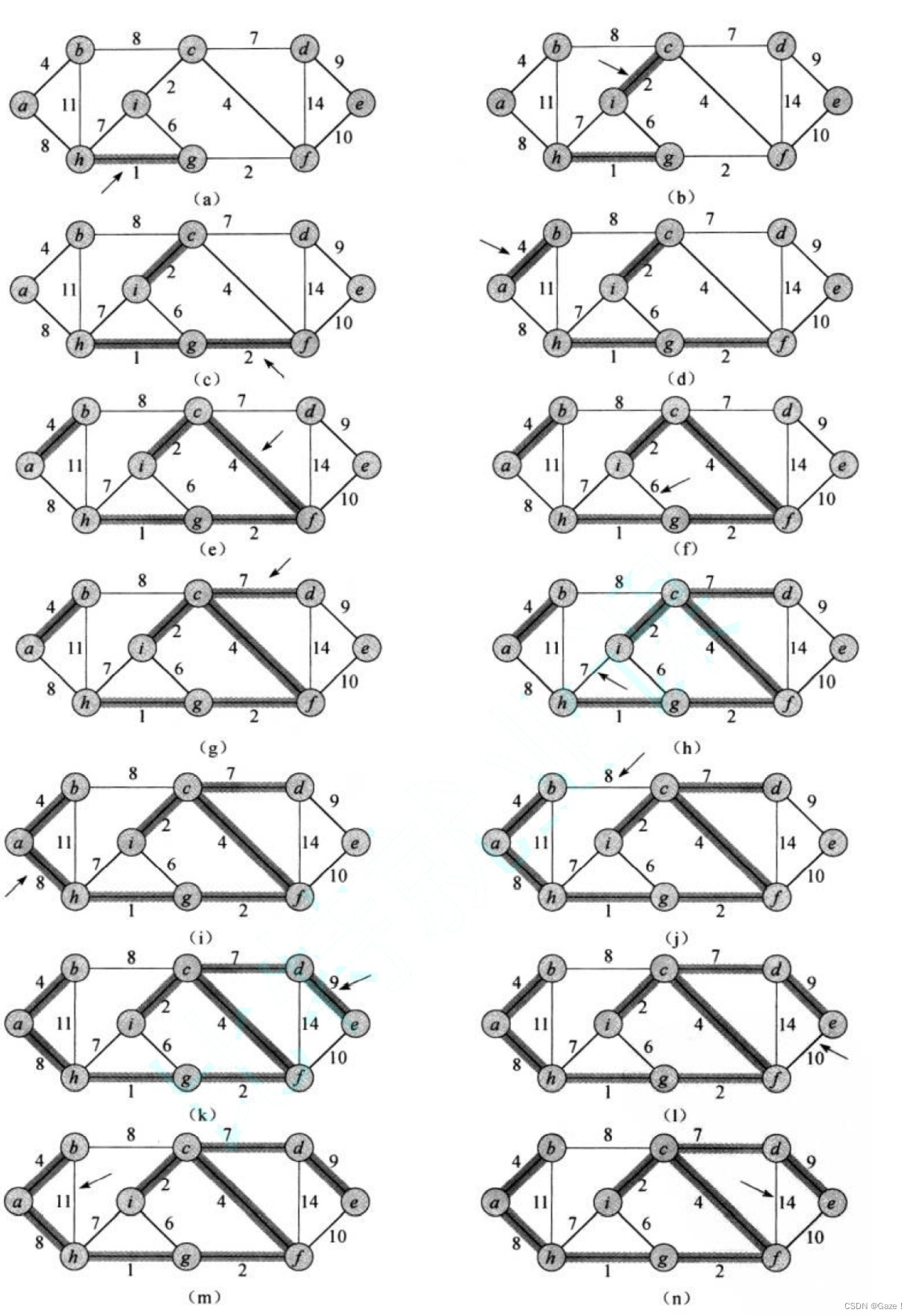
首先构造一个由这n个顶点组成、不含任何边的图G，其中每个顶点自成一个集合，其次不断取出权值最小的一条边(若有多条任取其一)，若该边的两个顶点来自不同的集合，则合并。如此重复，直到所有顶点在同一个集合。

---

 

 1.1.1模拟实现

Edge结构体

我们要选最小的边，需要选用的是优先级队列，那么首先需要保存的有边的权重，当我们选出一条边之后需要在最小生成树中添加这条边，所以需要起始位置和结束位置。

struct Edge
{
	size_t _srci;
	size_t _dsti;
	W _w;
	Edge(size_t srci, size_t dsti, const W& w)
		:_srci(srci)
        ,_dsti(dsti)
		,_w(w)
	{}
	bool operator>(const Edge& e)const
	{
		return _w > e._w;
	}
};

函数体

注：是实现在Graph类中的

W Kruskal(Self& minTree)
{
	size_t n = _vertexs.size(); //顶点数量
	//我传入的图 和 他生成树 的对应关系是一样的
	minTree._vertexs = _vertexs;
	minTree._indexMap = _indexMap;
	minTree._matrix.resize(n);
	for (int i = 0; i < n; i++)
	{
		minTree._matrix[i].resize(n,MAX_W);
	}

	priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
	//把所有边都入队列
	for (size_t i = 0; i < n; i++)
	{
		for (size_t j = 0; j < n; ++j)
		{
			if (i < j && _matrix[i][j] != MAX_W)
			{
				minque.push(Edge(i, j, _matrix[i][j]));
			}
		}
	}
	//一共n个顶点 我们只需要选n-1个顶点
	int size = 0;
	W total = W();
	UnionFindSet ufs(n);
	while (!minque.empty())
	{
		Edge min = minque.top();
		minque.pop();
		if (!ufs.InSet(min._srci, min._dsti))//起始地点和结束位置不在同一集合
		{
			ufs.Union(min._srci, min._dsti);
			minTree._AddEdge(min._srci, min._dsti, min._w);
			++size;
			total += min._w;
		}
	}
	if (size == n - 1)
	{
		return total;
	}
	else
	{
		return W();
	}
}

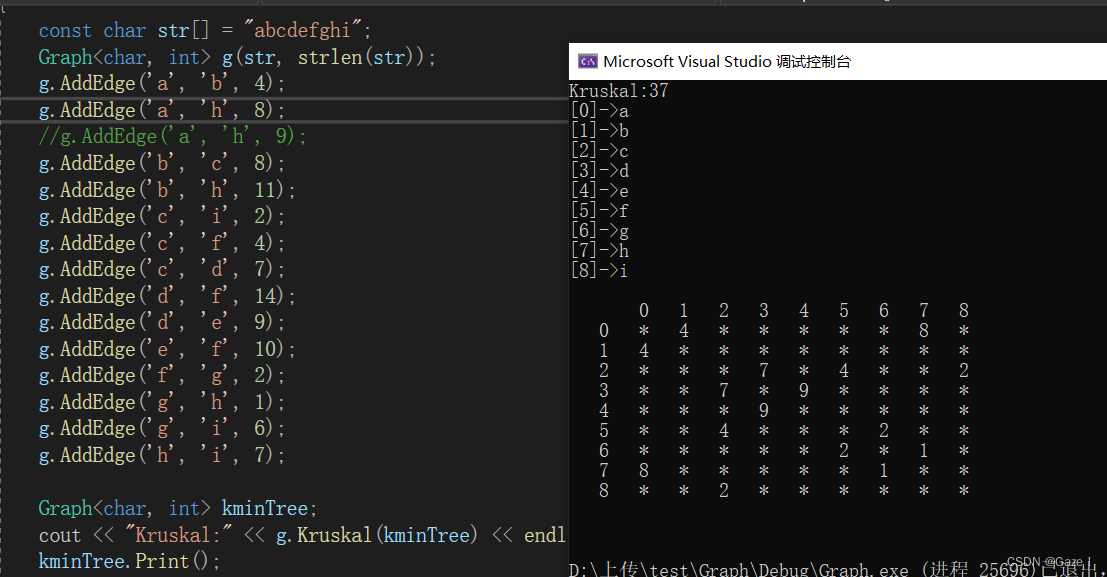
1.1.2测试代码及结果

 

---

 1.2 Prim

选一个起始节点，将总节点分为两个集合，一个已使用，一个未使用。每次在已使用节点中找一个权值最小的边链接，将终止节点纳入已使用节点。

1.2.1 代码主体

W Prim(Self& minTree, const W& src)
		{
			size_t srci = GetvertexIndex(src);
			size_t n = _vertexs.size();

			minTree._vertexs = _vertexs;
			minTree._indexMap = _indexMap;
			minTree._matrix.resize(n);
			for (size_t i = 0; i < n; ++i)
			{
				minTree._matrix[i].resize(n, MAX_W);
			}

			vector<bool> X(n, false);
			vector<bool> Y(n, true);
			//也可以选用两个set 目的是在查找集合中的值时快速

			X[srci] = true;
			Y[srci] = false;

			// 从X->Y集合中连接的边里面选出最小的边
			priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
			// 先把srci连接的边添加到队列中
			for (size_t i = 0; i < n; ++i)
			{
				if (_matrix[srci][i] != MAX_W)
				{
					minq.push(Edge(srci, i, _matrix[srci][i]));
				}
			}

			cout << "Prim开始选边" << endl;
			size_t size = 0;
			W totalW = W();
			while (!minq.empty())
			{
				Edge min = minq.top();
				minq.pop();

				// 最小边的目标点也在X集合，则构成环
				if (X[min._dsti])
				{
					//cout << "构成环:";
					//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;
				}
				else
				{
					minTree._AddEdge(min._srci, min._dsti, min._w);
					//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;
					X[min._dsti] = true;
					Y[min._dsti] = false;
					++size;
					totalW += min._w;
					if (size == n - 1)
						break;

					for (size_t i = 0; i < n; ++i)
					{
						if (_matrix[min._dsti][i] != MAX_W && Y[i])
						{
							minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));
						}
					}
				}
			}

			if (size == n - 1)
			{
				return totalW;
			}
			else
			{
				return W();
			}
		}