1.深度优先搜索(DFS)

深度优先搜索在搜索一个新的节点时，立即对新节点进行遍历，因此需要使用栈(先入后出)或递归来实现。

如下图：我们从1号节点开始遍历，假如遍历顺序是从左子节点到右子节点，那么按着深度优先遍历策略，假如我们使用递归实现，
我们的遍历过程为 1 (起始节点) --> 2 (遍历更深一层的左子节点) --> 4 (遍历更深一层的左子节点) --> 2 (无子节点,返回
父节点) --> 1 (子节点均已完成遍历,返回父节点) --> 3 (遍历更深一层的子节点) --> 1 (无子节点,返回父节点) -->
程序结束(子节点均已完成遍历)。假如我们使用栈实现，我们栈顶元素的变化过程为 1->2->4->3

深度优先也可以用来检测环路：记录每个遍历过的节点的父节点，若一个节点被再次遍历且父节点不同，则说明有环

（1）岛屿的最大面积(695)

给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例：

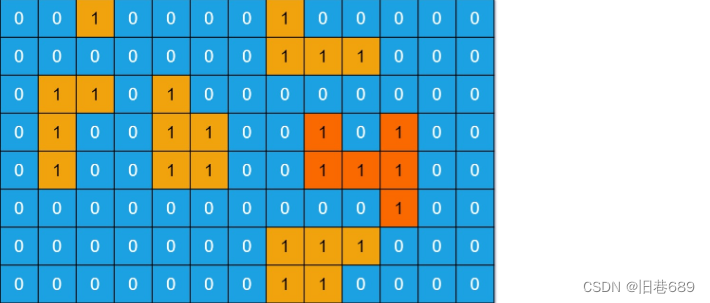
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

（1）遍历，当找到一块土地时，就以他的四个方向探索，探索经过的土地总数就是面积
（2）为了保证探索过的土地不再被访问，可以每次经过一块土地是，将 1 变为 0

public class test {

    public static void main(String[] args) {
        int[][] arr=new int[][]{{0,0,1,0,0,0,0,1,0,0,0,0,0},
                                {0,0,0,0,0,0,0,1,1,1,0,0,0},
                                {0,1,1,0,1,0,0,0,0,0,0,0,0},
                                {0,1,0,0,1,1,0,0,1,0,1,0,0},
                                {0,1,0,0,1,1,0,0,1,1,1,0,0},
                                {0,0,0,0,0,0,0,0,0,0,1,0,0},
                                {0,0,0,0,0,0,0,1,1,1,0,0,0},
                                {0,0,0,0,0,0,0,1,1,0,0,0,0}};
        int max = maxAreaOfIsland(arr);
        System.out.println(max);
    }

    public static int maxAreaOfIsland(int[][] grid) {
        int max=0;
        for (int i=0;i<grid.length;i++){
            for (int j=0;j<grid[0].length;j++){
                if (grid[i][j]==1){
                    max=Math.max(max,dfs(grid,i,j));
                }
            }
        }
        return max;
    }

    public static int dfs(int[][] arr,int i,int j){
        if (i<0||j<0||i>=arr.length||j>=arr[0].length||arr[i][j]!=1){
            return 0;
        }
        //已经经过的 1->0
        arr[i][j]=0;
        //某一块陆地的最大面积
        int sum=1;
        //递归求和4个方向
        sum+=dfs(arr,i-1,j);
        sum+=dfs(arr,i,j-1);
        sum+=dfs(arr,i+1,j);
        sum+=dfs(arr,i,j+1);
        return sum;
    }
}

（2）省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

因为是n*n的矩阵，所以根据题意城市的数量是n。所以我们可以维护一个大小为n的数组arr，初始时数组元素全为0。从矩阵第0
行开始遍历，开始判断此时的arr[i]是否为0，如果为0的话就省份数量+1，然后遍历第i行，找到元素本身为1且arr[j]不为1的
元素，令arr[j]=1(之后的外层循环就不在从这边进入)，然后递归调用j这个元素重复上述步骤

public class test {

    public static void main(String[] args) {
        int[][] isConnected=new int[][]{{1,1,0},
                                        {1,1,0},
                                        {0,0,1}};
        int provinceNum = findCircleNum(isConnected);
        System.out.println(provinceNum);
    }

    public static int findCircleNum(int[][] isConnected) {
        int provinceNum=0;
        int cityNum= isConnected.length;
        //城市相连关系表,int类型的数组默认初始化值为0
        int[] arr=new int[cityNum];
        //遍历行,也就是遍历每个城市
        for (int i=0;i<cityNum;i++){
            //如果某个城市还没有与其他城市形成省份
            if (arr[i]==0){
                //省份数量+1
                provinceNum++;
                //递归调用所有与这个城市可以形成省份的城市,将它们都置为1
                dfs(isConnected,arr,cityNum,i);
            }
        }
        return provinceNum;
    }

    private static void dfs(int[][] isConnected, int[] arr, int cityNum, int i) {
        //遍历列,也就是这个城市和其他城市的关系
        for (int j=0;j<cityNum;j++){
            //如果遇到与这个城市相连的城市而且还不在关系表中
            if (isConnected[i][j]==1&&arr[j]==0){
                //将其加入关系表
                arr[j]=1;
                //并且对这个城市再次递归调用
                dfs(isConnected,arr,cityNum,j);
            }
        }
    }
}

（3）太平洋大西洋水流问题(417)

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

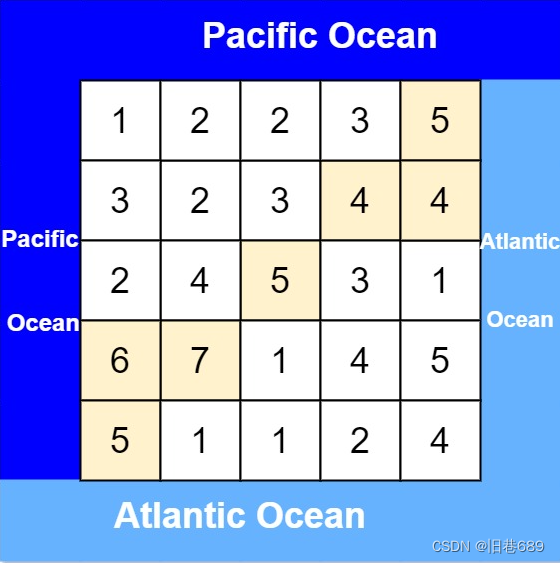
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

直接以每个单元格开始遍历整个地图貌似会超时，因为会重复遍历单元格。为了降低时间复杂度，可以从矩阵的边界开始反向搜索
寻找雨水流向边界的单元格，反向搜索时，每次只能移动到相同高度或更大的单元格。
从矩阵的左边界和上边界开始反向搜索即可找到流向太平洋的单元格，从矩阵的右边界和下边界开始反向搜索即可得到雨水流向大
西洋的单元格。
反向搜索结束之后，遍历每个网格，如果一个网格既可以从太平洋反向到达也可以从大西洋反向到达，则该网格满足太平洋和大西
洋都可以到达。

public class test {

    public static void main(String[] args) {
        int[][] arr=new int[][]{{1,2,2,3,5},
                                {3,2,3,4,4},
                                {2,4,5,3,1},
                                {6,7,1,4,5},
                                {5,1,1,2,4}};
        List<List<Integer>> listList = pacificAtlantic(arr);
        for (List<Integer> list:listList){
            for (int cell:list){
                System.out.print(cell+" ");
            }
            System.out.println();
        }
    }

    public static List<List<Integer>> pacificAtlantic(int[][] heights) {
        //递归遍历的方向 [0]:行 [1]:列
        int[][] dirs={{-1,0},{1,0},{0,-1},{0,1}};
        int totalRows= heights.length;//总行数
        int totalCols=heights[0].length;//总列数
        //雨水可以流向太平洋的单元格 boolean数组默认初始值为false
        boolean[][] pacific=new boolean[totalRows][totalCols];
        //雨水可以流向大西洋的单元格 boolean数组默认初始值为false
        boolean[][] atlantic=new boolean[totalRows][totalCols];

        //从左边界反向搜索
        for (int i=0;i<totalRows;i++){
            dfs(i,0,pacific,totalRows,totalCols,dirs,heights);
        }
        //从上边界反向搜索 左上角那个单元格不用重复搜索
        for (int j=1;j<totalCols;j++){
            dfs(0,j,pacific,totalRows,totalCols,dirs,heights);
        }
        //从右边界反向搜索
        for (int i=0;i<totalRows;i++){
            dfs(i,totalCols-1,atlantic,totalRows,totalCols,dirs,heights);
        }
        //从下边界反向搜索 右下角那个单元格不用重复搜索
        for (int j=0;j<totalCols-1;j++){
            dfs(totalRows-1,j,atlantic,totalRows,totalCols,dirs,heights);
        }
        List<List<Integer>> result= new ArrayList<>();
        //遍历单元格找出既可以到达太平洋又可以到达大西洋的
        for (int i=0;i<totalRows;i++){
            for (int j=0;j<totalCols;j++){
                if (pacific[i][j]&&atlantic[i][j]){
                    List<Integer> cell=new ArrayList<>();
                    cell.add(i);
                    cell.add(j);
                    result.add(cell);
                }
            }
        }
        return result;
    }

    private static void dfs(int row, int col, boolean[][] ocean, int totalRows, int totalCols, int[][] dirs, int[][] heights) {
        if (ocean[row][col]){
            return;
        }
        ocean[row][col]=true;
        //从四个方向开始递归遍历
        for (int[] dir:dirs){
            int newRow=row+dir[0];
            int newCol=col+dir[1];
            if (newRow>=0&&newRow<totalRows&&newCol>=0&&newCol<totalCols&&heights[newRow][newCol]>=heights[row][col]){
                dfs(newRow,newCol,ocean,totalRows,totalCols,dirs,heights);
            }
        }
    }
}

2.回溯法

回溯法是优先搜索的一种特殊情况，又称为试探法，常用于需要记录节点状态的深度优先搜索。
在搜索到某一结点的时候，如果发现目前的节点(及其子节点)并不是需求目标时，我们回退到原来的节点继续搜索，并且把目前节点
修改的状态还原。这样的好处是我们可以始终对图的总状态进行修改，而非每次遍历时新建一个图来存储状态。
回溯算法用于搜索一个问题的所有的解，通过深度优先遍历的思想实现

（1）全排列(46)

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列 。你可以按任意顺序返回答案。

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

输入：nums = [0,1]
输出：[[0,1],[1,0]]

输入：nums = [1]
输出：[[1]]

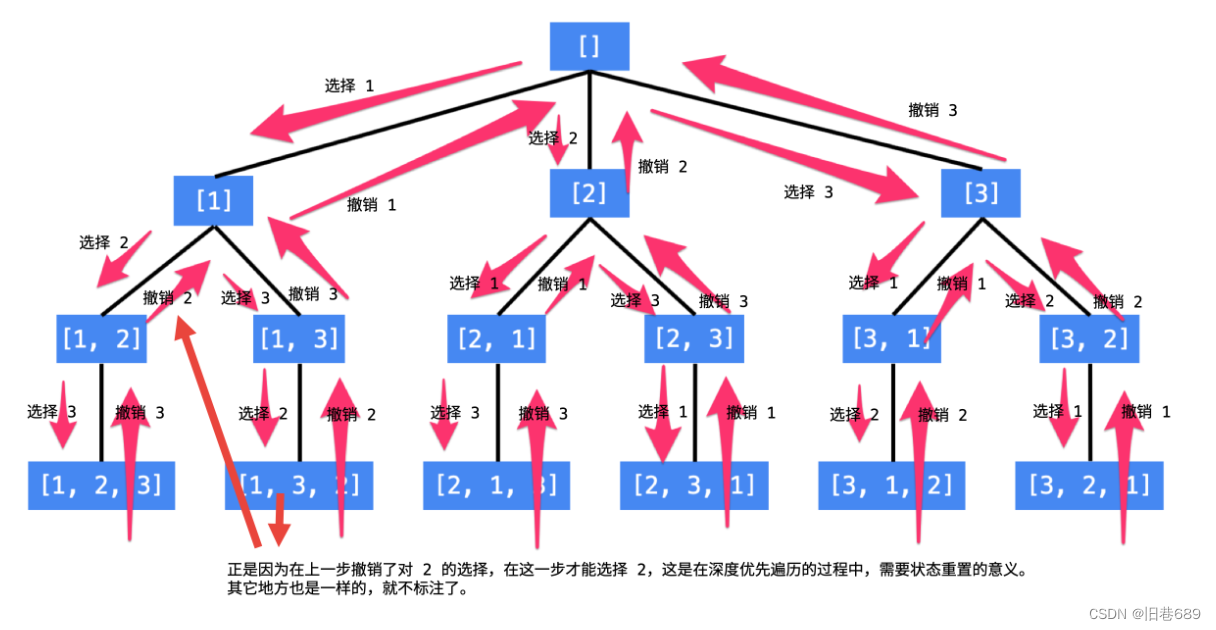图片来自: https://leetcode.cn/problems/permutations/solutions/9914/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/

public class test {

    public static void main(String[] args) {
        int[] arr=new int[]{1,2,3};
        List<List<Integer>> listList = permute(arr);
        System.out.println(listList);
    }

    public static List<List<Integer>> permute(int[] nums) {
        //定义一个链表保存所有可能的全排列
        List<List<Integer>> res=new ArrayList<>();
        //如果nums为空,返回空的链表res
        if (nums.length==0){
            return res;
        }
        //定义一个标记数组,标记该数是否已经填过 默认为false
        boolean[] used=new boolean[nums.length];
        //定义一个链表,保存当前的全排列
        List<Integer> path=new ArrayList<>();

        dfs(nums,0,res,used,path);
        return res;
    }

    private static void dfs(int[] nums, int depth, List<List<Integer>> res, boolean[] used, List<Integer> path) {
        //递归退出条件
        if (depth== nums.length){
            res.add(new ArrayList<>(path));
            return;
        }

        //在还未选择的数中依次选择一个元素作为下一个位置的元素
        for (int i=0;i< nums.length;i++){
            if (!used[i]){
                //链表中加入这个元素
                path.add(nums[i]);
                //标记这个元素
                used[i]=true;
                //递归调用
                dfs(nums,depth+1,res,used,path);
                //回溯
                used[i]=false;
                path.remove(path.size()-1);
            }
        }
    }
    
}

（2）组合(77)

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

输入：n = 1, k = 1
输出：[[1]]

如果解决一个问题有多个步骤，每一个步骤有多种方法，题目有要求找出所有的方法，可以使用回溯算法
回溯算法首先要画递归树，不同的树决定了不同的代码实现。

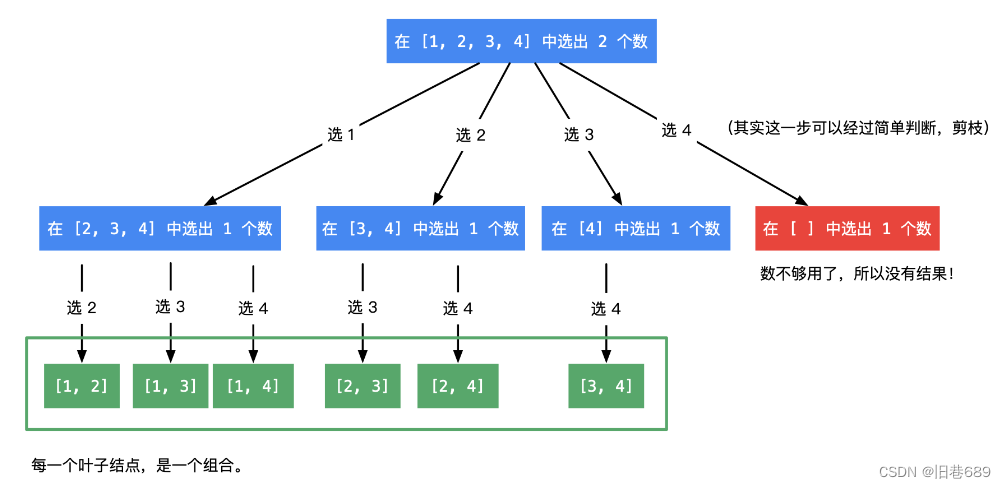
图片来自: https://leetcode.cn/problems/combinations/solutions/13436/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-ma-/

public class test {

    public static void main(String[] args) {
        int n=4;
        int k=2;
        List<List<Integer>> list = combine(n, k);
        System.out.println(list);
    }

    public static List<List<Integer>> combine(int n, int k) {
        //链表用来存储所有可能的组合
        List<List<Integer>> res = new ArrayList<>();
        //可以不加这个判断,因为LeetCode中给出了边界条件
        if (n < 1 || k > n) {
            return res;
        }
        //双端队列用来存储一个组合
        Deque<Integer> path = new ArrayDeque<>();
        //题目要求从1开始
        dfs(n,k,1,res,path);
        return res;
    }

    private static void dfs(int n, int k, int begin, List<List<Integer>> res, Deque<Integer> path) {
        //递归结束条件
        if (path.size()==k){
            res.add(new ArrayList<>(path));
            return;
        }

        //遍历所有可能的起点
        for (int i=begin;i<=n;i++){
            //加入一个数进入path
            path.addLast(i);
            //下一轮搜索,设置搜索的起点要加1
            dfs(n,k,i+1,res,path);
            //还原之前的数组
            path.removeLast();
        }
    }
}

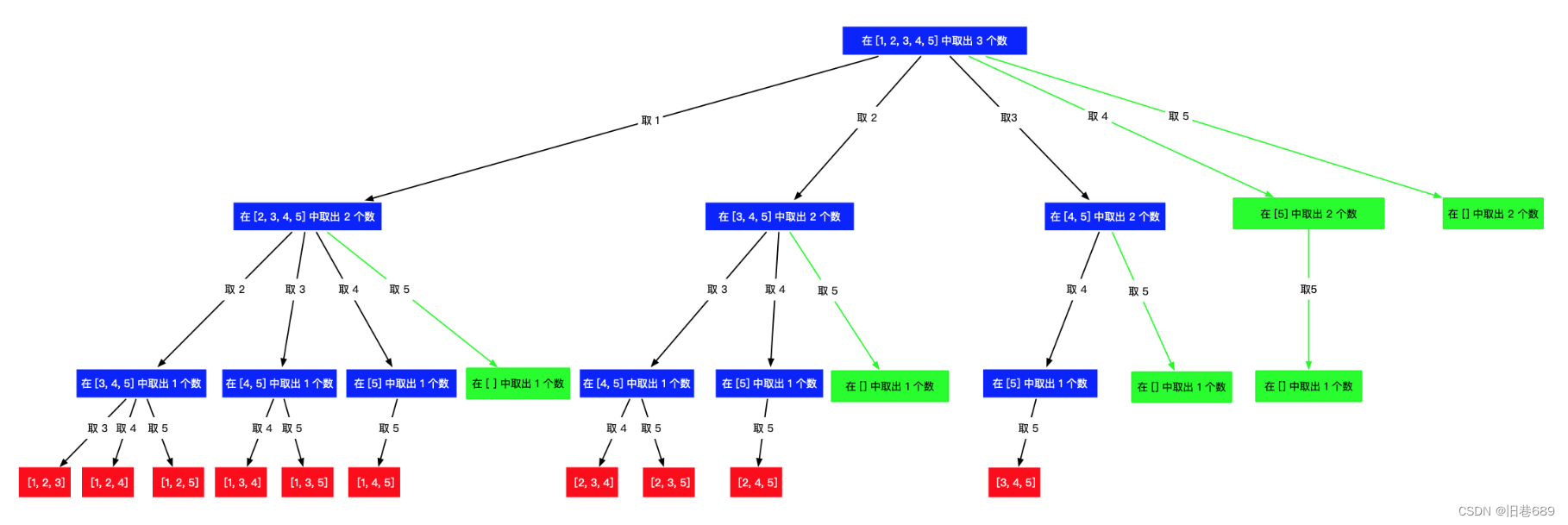
之前的代码是一直遍历到n，其实这样就会出现遍历一些没有意义的数，增加时间复杂度，可以在深度优先遍历的过程中进行
剪枝，这样可以避免不必要的遍历

我们可以知道：搜索起点和当前还需要选几个数有关，而当前还需要选几个数与已经选好了几个数有关
例如：n=7,k=3
path.size()==1时，还可以选择两个数，则最大的搜索起点是6，最后一个被选中的组合是 [6,7]
path.size()==2时，还可以选择1个数，则最大的搜索起点是7，最后一个被选中的组合是 [7]
我们可以归纳出：搜索的上界：n-(k-path.size())+1
所以可以将i<=n改为i<=n-(k-path.size())+1

（3）单词搜索(79)

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

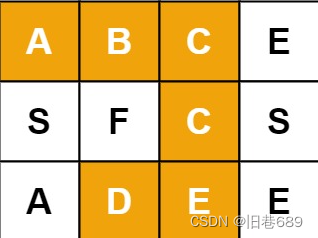
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

对一个元素的上下左右搜索，搜索不匹配时，回溯，考虑上一个状态的其他方向，如果走完都没有匹配到，那么从下一个元素开始
继续匹配，如果匹配到了，直接返回true

public class test {

    private static final int[][] DIRECTIONS={{-1,0},{1,0},{0,-1},{0,1}};
    private boolean[][] visited;

    public static void main(String[] args) {
        char[][] arr={{'A','B','C','E'},
                      {'S','F','C','S'},
                      {'A','D','E','E'}};
        String word="ABCCED";
        test t=new test();
        System.out.println(t.exist(arr,word));
    }

    public boolean exist(char[][] board, String word) {
        if (board.length==0){
            return false;
        }
        char[] chars = word.toCharArray();
        //初始化visited数组,默认初始化元素为false
        visited=new boolean[board.length][board[0].length];
        //遍历二维网格中每一个字母,从此字母开始是否可以找到word
        for (int i=0;i< board.length;i++){
            for (int j=0;j<board[0].length;j++){
                //递归调用
                if (dfs(i,j,0,chars,board)){
                    return true;
                }
            }
        }
        return false;
    }

    private boolean dfs(int i, int j, int begin, char[] chars, char[][] board) {
        //递归结束条件,如果到单词最后一个字母,就和网格当前字符比较,如果相等返回true,否则返回false
        if (begin== chars.length-1){
            return chars[begin]==board[i][j];
        }
        if (chars[begin]==board[i][j]){
            //标记当前元素已经搜索过了
            visited[i][j]=true;
            //在当前元素四个方向上搜索
            for (int[] direction:DIRECTIONS){
                int newI=i+direction[0];
                int newJ=j+direction[1];
                //边界条件与visited数组皆满足
                if (newI>=0&&newI< board.length&&newJ>=0&&newJ<board[0].length&&!visited[newI][newJ]){
                    //递归搜索
                    if (dfs(newI,newJ,begin+1,chars,board)){
                        return true;
                    }
                }
            }
            //还原当前元素
            visited[i][j]=false;
        }
        return false;
    }
}

（4）N 皇后(51)

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

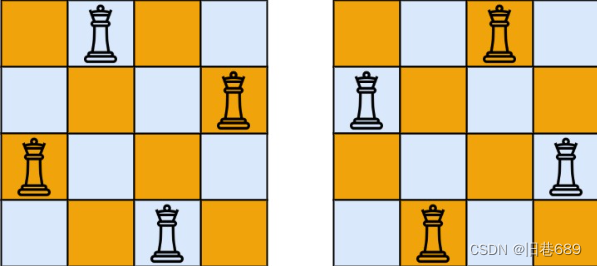
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

有题目要求可知，在每一行同一列以及同一斜线上只能存在一个皇后。

由于暴力枚举时间复杂度会很高，所以可以考虑使用回溯的方式寻找解。使用一个数组记录每行位置放置的皇后的列下标，依次在
每一行放置一个皇后。每次新放置的皇后不能和已经放置的皇后在同一列以及同一条斜线上，并更新数组中的当前行的皇后列下标。
当N个皇后都放置完毕，则找到一个可能的解。当找到一个可能的解后，将数组转换成表示棋盘状态的列表，并将该棋盘状态的列表
加入返回列表。由于每个皇后必须位于不同列，因此已经放置的皇后所在的列不能放置别的皇后。第一个皇后有N个选择，第二个最
多有N-1个选择，以此类推，因此遍历所有情况的时间复杂度是O(n!)。

为了降低总时间复杂度，每次放置皇后时需要快速判断每个位置是否可以放置皇后，可以使用集合或者位运算对皇后的位置进行判断。
都可以在O(1)的时间内判断一个位置是否可以放置皇后，总的时间复杂度是O(n!)。

（1）基于集合的回溯：
为了判断一个位置所在的列和两条斜线上是否已经有皇后，使用三个集合columns diagonals1 diagonals2分别记录每一列
以及两个方向的每条斜线上是否有皇后。
列使用下标即可明确表示每一列
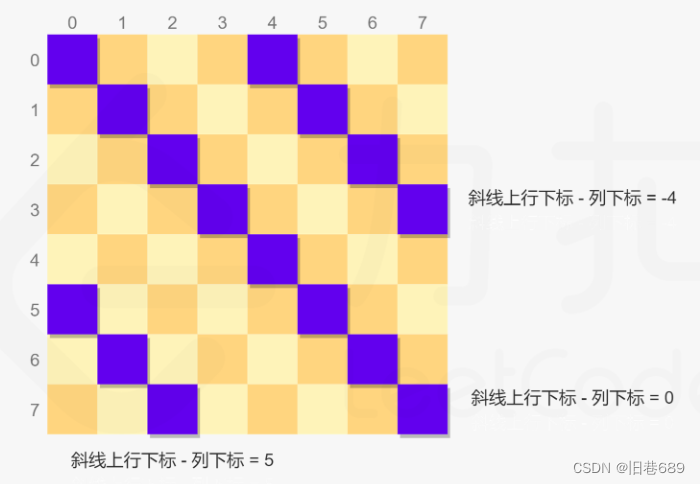
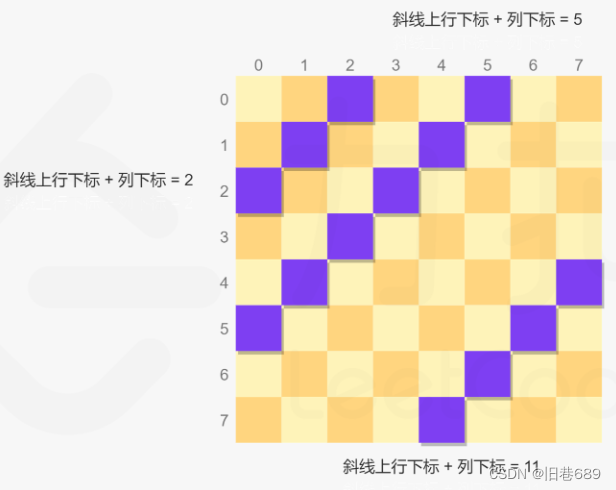
斜线为左上到右下时：同一条斜线上的每个位置满足行下标与列下标之差相等
斜线为右上到左下时：同一条斜线上的每个位置满足行下标与列下标之和相等
每次放置皇后时，对于每个位置判断其是否在三个集合中，如果三个集合都不包含当前位置，则当前位置可以放置皇后

public class test {

    public static void main(String[] args) {
        int n=4;
        test t=new test();
        System.out.println(t.solveNQueens(n));
    }

    public List<List<String>> solveNQueens(int n) {
        //定义一个集合保存最后的输出
        List<List<String>> solutions=new ArrayList<>();
        //保存每一种解决方案皇后的位置
        int[] queenDir=new int[n];
        //保存哪些列不能放皇后的信息
        Set<Integer> columns=new HashSet<>();
        //保存哪些左上到右下的斜线不能放皇后的信息
        Set<Integer> diagonals1=new HashSet<>();
        //保存哪些右上到左下的斜线不能放皇后的信息
        Set<Integer> diagonals2=new HashSet<>();
        //递归求结果 从第0行开始
        dfs(0,n,queenDir,solutions,columns,diagonals1,diagonals2);
        return solutions;
    }

    private void dfs(int row, int n, int[] queenDir, List<List<String>> solutions, Set<Integer> columns, Set<Integer> diagonals1, Set<Integer> diagonals2) {
        //可以来到最后一行,证明可以找到一个解决方案,将其加入解决方案集合中
        if (row==n){
            //根据皇后的位置,转换出输出结果
            List<String> board=changeBoard(queenDir,n);
            solutions.add(board);
        }else {
            //表示列
            for (int i=0;i<n;i++){
                //如果该列已经有皇后了
                if (columns.contains(i)){
                    //强制跳过当前循环剩下的语句,执行下一次循环
                    continue;
                }
                //如果该左上到右下的斜线已经有皇后了
                int diagonal1=row-i;
                if (diagonals1.contains(diagonal1)){
                    continue;
                }
                //如果该右上到左下的斜线已经有皇后了
                int diagonal2=row+i;
                if (diagonals2.contains(diagonal2)){
                    continue;
                }
                //row行的皇后位置在i列
                queenDir[row]=i;
                //将当前皇后的位置信息加入三个信息集合
                columns.add(i);
                diagonals1.add(diagonal1);
                diagonals2.add(diagonal2);
                //开始递归遍历下一行
                dfs(row+1,n,queenDir,solutions,columns,diagonals1,diagonals2);
                //一次解决方案寻找结束,回溯,继续下一次
                queenDir[row]=-1;
                columns.remove(i);
                diagonals1.remove(diagonal1);
                diagonals2.remove(diagonal2);
            }
        }
    }

    private List<String> changeBoard(int[] queenDir, int n) {
        List<String> board=new ArrayList<>();
        for (int i=0;i<n;i++){
            char[] ch=new char[n];
            //将ch[i]中的元素全部初始化为 "." 初始化完成之后就是 n个"."
            Arrays.fill(ch,'.');
            //找到queenDir中i位置存储的数字,就是皇后在这一行出现的位置,将ch数组中这个位置的"."改为"Q"
            ch[queenDir[i]]='Q';
            board.add(new String(ch));
        }
        return board;
    }
}

3.广度优先遍历

广度优先遍历是一层层进行遍历的，因此需要用先入先出的队列进行遍历，也常常用来处理最短路径等问题。
如下图所示的二叉树：我们从1号节点开始遍历，加入遍历顺序是从左节点到右节点，那么队列顶端元素的变化过程为：[1] ->
[2->3] -> [4]

（1）最短的桥(934)

给你一个大小为 n x n 的二元矩阵 grid ，其中 1 表示陆地，0 表示水域。

岛 是由四面相连的 1 形成的一个最大组，即不会与非组内的任何其他 1 相连。grid 中 恰好存在两座岛 。

你可以将任意数量的 0 变为 1 ，以使两座岛连接起来，变成 一座岛 。

返回必须翻转的 0 的最小数目。

输入：grid = [[0,1],[1,0]]
输出：1

输入：grid = [[0,1,0],[0,0,0],[0,0,1]]
输出：2

输入：grid = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
输出：1

可以利用深度优先搜索求出其中的一座岛，然后利用广度优先搜索来找到两座岛的最大距离
（1）通过遍历找到数据grid中的1后进行深度优先遍历，此时可以找到第一座岛的位置集合，记为island，并将其全部位置标
记为2
（2）随后从island中的所有位置开始进行广度优先搜索，当它们到达了任意的1时，即表示搜索到了第二个岛，搜索的层数就是
答案。

public class test {

    public static void main(String[] args) {
        int[][] arr={{0,1},{1,0}};
        test t=new test();
        System.out.println(t.shortestBridge(arr));
    }

    public int shortestBridge(int[][] grid) {
        //方向数组,广度优先遍历时,可以向四个方向都发散一次
        int[][] dirs={{-1,0},{1,0},{0,-1},{0,1}};
        int n= grid.length;
        for (int i=0;i< n;i++){
            for (int j=0;j<n;j++){
                //如果遍历的时候找到第一个1,就开始执行操作
                if (grid[i][j]==1){
                    //创建一个队列,用来保存第一座岛的位置信息
                    Queue<int[]> queue=new ArrayDeque<>();
                    //递归调用,得到第一座岛的信息
                    dfs(i,j,queue,grid);
                    //需要将0变为1的数量
                    int step=0;
                    //根据队列里保存的信息开始广度优先遍历
                    while (!queue.isEmpty()){
                        //当前队列的大小
                        int size = queue.size();
                        //依次遍历当前队列的每一个元素
                        for (int k=0;k<size;k++){
                            //弹出队首元素
                            int[] poll = queue.poll();
                            //当前元素在grid中的位置
                            int x=poll[0];
                            int y=poll[1];
                            //当前元素的四个方向都要遍历
                            for (int[] dir:dirs){
                                //需要向外遍历的位置
                                int newX=x+dir[0];
                                int newY=y+dir[1];
                                //判断向外扩展的位置是否合法
                                if (newX>=0&&newX<n&&newY>=0&&newY<n){
                                    if (grid[newX][newY]==0){
                                        //将这个位置信息加入队列
                                        queue.add(new int[]{newX,newY});
                                        //将这个位置的数字改为2
                                        grid[newX][newY]=2;
                                    }else if(grid[newX][newY]==1){//如果找到下一个岛
                                        //返回最小数目
                                        return step;
                                    }
                                }
                            }
                        }
                        //如果第一轮广度优先遍历没有找到下一个岛屿,就将0变为1的数量+1，继续下一次广度优先遍历
                        step++;
                    }
                }
            }
        }
        return 0;
    }

    private void dfs(int i, int j, Queue<int[]> queue, int[][] grid) {
        if (i<0||i>= grid.length||j<0||j>= grid.length||grid[i][j]!=1){
            return;
        }
        //将位置信息加入队列
        queue.add(new int[]{i,j});
        //将当前位置值改为2
        grid[i][j]=2;
        //四个方向递归遍历
        dfs(i-1,j,queue,grid);
        dfs(i+1,j,queue,grid);
        dfs(i,j-1,queue,grid);
        dfs(i,j+1,queue,grid);
    }
}

（2）单词接龙(127)

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk：

每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

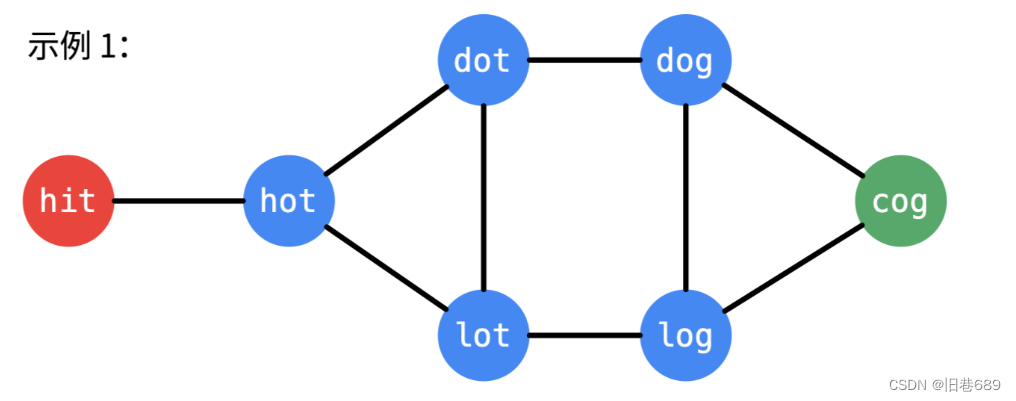
输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。

提示：
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同

题目中给出的单词与单词之间的关系构成了一张无向图，无向图两个顶点之间的最短路径的长度，可以通过广度优先遍历得到。

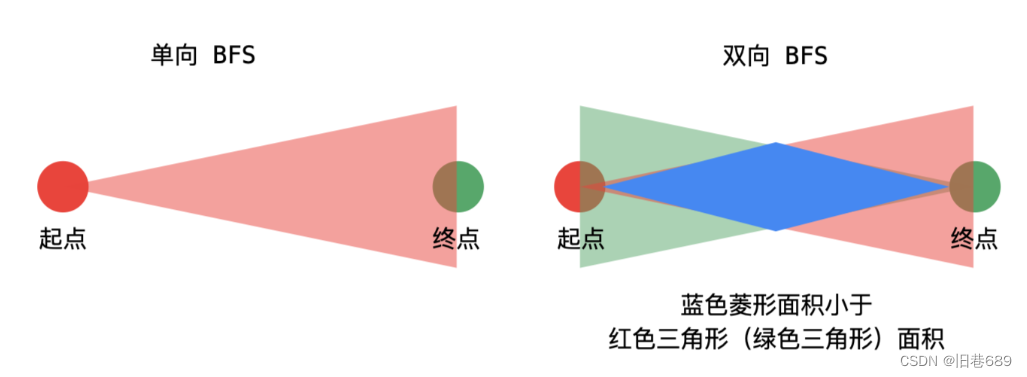
因为目标顶点已知，可以分别从起点和目标顶点执行广度优先遍历，直到遍历的部分有交集，这是双向广度优先遍历的思想。

如果一开始就构建图，每一个单词都需要和除它以外的另外单词进行比较，复杂度是O(NM)，N：单词列表的长度，M：单词的长度

为此，我们在遍历一开始，把所有的单词列表放进一个哈希表中，然后在遍历的时候构件图，每一次得到在单词列表里可以转换的
单词，复杂度是O(26*M)，借助哈希表，找到领居与N无关

需要的辅助数据结构：（1）队列；
				 （2）集合 说明：可以直接在wordSet(由wordList放进集合中得到)里做删除。但更好的做法是新开一个
				     哈希表，遍历过的字符串放进哈希表里。

在目标顶点已知的情况下，可以分别从起点和目标顶点执行广度优先遍历，直到遍历的部分有交集，这种方式搜索的单词数量会更小
一些；每次从单词数量小的集合开始扩散；

public class test {

    public static void main(String[] args) {
        String beginWord="hit";
        String endWord="cog";
        List<String> wordList=new ArrayList<>();
        wordList.add("hot");
        wordList.add("dot");
        wordList.add("dog");
        wordList.add("lot");
        wordList.add("log");
        wordList.add("cog");
        test t=new test();
        System.out.println(t.ladderLength1(beginWord,endWord,wordList));
    }

    //广度优先遍历
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        //建立一个哈希表,便于判断某个单词是否在wordList中 Set:去重,将wordList中重复的单词去掉
        Set<String> wordSet=new HashSet<>(wordList);
        //如果为空或者没有目标单词 直接返回0
        if (wordSet.size()==0||!wordSet.contains(endWord)){
            return 0;
        }
        //如果单词列表里第一个单词,就去掉
        wordSet.remove(beginWord);

        //图的广度优先遍历,必须使用队列和表示是否访问过的visited哈希表
        Queue<String> queue=new LinkedList<>();
        queue.add(beginWord);
        Set<String> visited=new HashSet<>();
        visited.add(beginWord);

        //开始广度优先遍历,包含起点,因此初始化的时候步数为1
        int step=1;
        while (!queue.isEmpty()){//遍历
            //本次遍历queue的大小,之后可能会因为新加入元素而改变大小
            int currentSize= queue.size();
            for (int i=0;i<currentSize;i++){
                //依次遍历当前队列的单词
                String currentWord = queue.poll();
                //如果currentWord能够修改1个字符与endWord相同,则返回step+1
                if (changeWordEveryOneLetter(currentWord,endWord,queue,visited,wordSet)){
                    return step+1;
                }
            }
            //如果没有成功匹配到endWord,步数+1
            step++;
        }

        //如果遍历完单词列表也没匹配到,就返回0
        return 0;
    }

    /**
     * 对currentWord修改每一个字符,看看是不是能与endWord匹配
     * @param currentWord
     * @param endWord
     * @param queue
     * @param visited
     * @param wordSet
     * @return
     */
    private boolean changeWordEveryOneLetter(String currentWord, String endWord, Queue<String> queue, Set<String> visited, Set<String> wordSet) {
         char[] charArray=currentWord.toCharArray();
         //分别修改每一个字符
        for (int i=0;i< charArray.length;i++){
            //先保存当前字符,最后恢复
            char originChar=charArray[i];
            //将当前字符分别替换成其余25个字符
            for (char j='a';j<='z';j++){
                if (originChar==j){
                    continue;
                }
                charArray[i]=j;
                //转换后的单词
                String nextWord=String.valueOf(charArray);
                if (wordSet.contains(nextWord)){
                    //如果转换后的单词恰好等于endWord
                    if (nextWord.equals(endWord)){
                        return true;
                    } else if (!visited.contains(nextWord)) {
                        queue.add(nextWord);
                        //添加到队列后,标记为已访问
                        visited.add(nextWord);
                    }
                }
            }
            //恢复
            charArray[i]=originChar;
        }
         return false;
    }


    //双向广度优先遍历
    public int ladderLength1(String beginWord, String endWord, List<String> wordList) {
        //将wordList放到哈希表里,便于判断某个词是否在wordList中
        Set<String> wordSet=new HashSet<>(wordList);
        if (wordSet.size()==0||!wordSet.contains(endWord)){
            return 0;
        }

        //已经访问过的单词加入visited哈希表里
        Set<String> visited=new HashSet<>();
        //分别用左边和右边扩散的哈希表代替单向BFS里的队列,它们在双向BFS的过程中交替使用
        Set<String> beginVisited=new HashSet<>();
        beginVisited.add(beginWord);
        Set<String> endVisited=new HashSet<>();
        endVisited.add(endWord);

        //执行双向BFS,左右交替扩散的步数之和为要求的数目
        int step=1;
        while (!beginVisited.isEmpty()&&!endVisited.isEmpty()){
            //优先选择小的哈希表进行扩散,考虑到的情况更少
            if (beginVisited.size()> endVisited.size()){
                //交换beginVisited和endVisited
                Set<String> temp=beginVisited;
                beginVisited=endVisited;
                endVisited=temp;
            }

            //现在beginVisited是相对较小的集合,nextLevelVisited在扩散完成以后,会成为新的beginVisited
            Set<String> nextLevelVisited=new HashSet<>();
            for (String word:beginVisited){
                if (changeWordEveryOneLetter1(word,endVisited,visited,wordSet,nextLevelVisited)){
                    return step+1;
                }
            }

            //原来的beginVisited废弃,从nextLevelVisited开始新的双向BFS
            beginVisited=nextLevelVisited;
            step++;
        }

        return 0;
    }

    /**
     * 尝试对word修改每一个字符,看看是不是能落在endVisited中,扩展得到的新的word添加到nextLevelVisited里
     * @param word
     * @param endVisited
     * @param visited
     * @param wordSet
     * @param nextLevelVisited
     * @return
     */
    private boolean changeWordEveryOneLetter1(String word, Set<String> endVisited, Set<String> visited, Set<String> wordSet, Set<String> nextLevelVisited) {
        char[] charArray=word.toCharArray();
        for (int i=0;i<charArray.length;i++){
            char originChar=charArray[i];
            for (char j='a';j<='z';j++){
                if (originChar==j){
                    continue;
                }
                charArray[i]=j;
                String nextWord=String.valueOf(charArray);
                if (wordSet.contains(nextWord)){
                    if (endVisited.contains(nextWord)){
                        return true;
                    }
                    if (!visited.contains(nextWord)){
                        nextLevelVisited.add(nextWord);
                        visited.add(nextWord);
                    }
                }
            }
            //恢复,下次使用
            charArray[i]=originChar;
        }
        return false;
    }
}

（3）单词接龙2(126)

按字典 wordList 完成从单词 beginWord 到单词 endWord 转化，一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> … -> sk 这样的单词序列，并满足：

每对相邻的单词之间仅有单个字母不同。
转换过程中的每个单词 si（1 <= i <= k）必须是字典 wordList 中的单词。注意，beginWord 不必是字典 wordList 中的单词。
sk == endWord
给你两个单词 beginWord 和 endWord ，以及一个字典 wordList 。请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列 ，如果不存在这样的转换序列，返回一个空列表。每个序列都应该以单词列表 [beginWord, s1, s2, …, sk] 的形式返回。

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：[["hit","hot","dot","dog","cog"],["hit","hot","lot","log","cog"]]
解释：存在 2 种最短的转换序列：
"hit" -> "hot" -> "dot" -> "dog" -> "cog"
"hit" -> "hot" -> "lot" -> "log" -> "cog"

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：[]
解释：endWord "cog" 不在字典 wordList 中，所以不存在符合要求的转换序列。

提示：
1 <= beginWord.length <= 5
endWord.length == beginWord.length
1 <= wordList.length <= 500
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有单词 互不相同

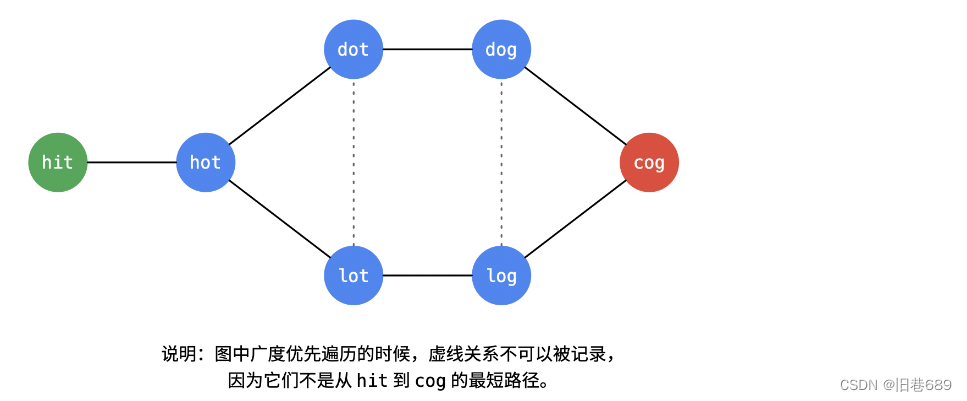
题目中给出的单词与单词之间的关系构成了一张无向图，题目要求求最短转换序列，也就是要求最短路径，我们可以使用广度
优先遍历。然后题目有要求返回所有的最短序列，那么我们就需要使用回溯算法每一次求完都恢复成之前的状态。

public class test {

    public static void main(String[] args) {
        
    }

    public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
        //保存所有的最短路径
        List<List<String>> res=new ArrayList<>();
        //将wordList存入哈希表,用来快速判断拓展出的单词是否在wordList里
        Set<String> dict=new HashSet<>(wordList);
        //如果wordList中不存在endWord,那么就直接返回空的res
        if (!dict.contains(endWord)){
            return res;
        }
        //因为从beginWord开始拓展,所有dict中不能有beginWord
        dict.remove(beginWord);

        //广度优先遍历构建图
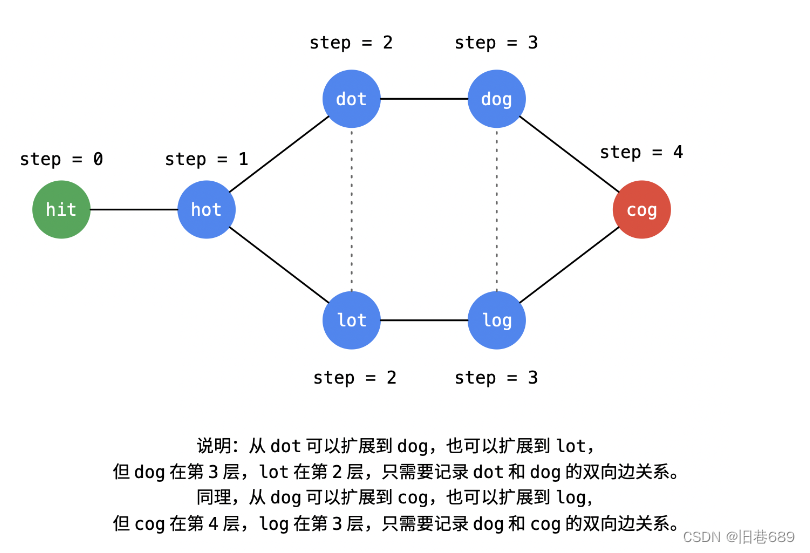
        //为了避免记录不需要的边,我们需要记录拓展出的单词是在第几次拓展的时候得到的,key:单词,value:
        //steps记录了已经访问过的word集合,同时记录了在第几层访问到
        Map<String,Integer> steps=new HashMap<>();
        steps.put(beginWord,0);
        //from记录单词是从哪些单词扩展而来,key:单词,value:单词列表,这些单词可以变换到key,它们是一对多的关系
        Map<String,Set<String>> from =new HashMap<>();
        boolean found=bfs(beginWord,endWord,dict,steps,from);

        //深度优先遍历找到所有解,从endWord恢复到beginWord,所以每次尝试操作path列表的头部
        if (found){
            Deque<String> path=new ArrayDeque<>();
            path.add(endWord);
            dfs(from,path,beginWord,endWord,res);
        }

        return res;
    }

    private boolean bfs(String beginWord, String endWord, Set<String> dict, Map<String, Integer> steps, Map<String, Set<String>> from) {
        int wordLen=beginWord.length();
        int step=0;
        boolean found=false;

        Queue<String> queue=new LinkedList<>();
        queue.add(beginWord);
        while (!queue.isEmpty()){
            step++;
            //当前队列的大小
            int size= queue.size();
            for (int i=0;i<size;i++){
                String currWord=queue.poll();
                char[] charArray=currWord.toCharArray();
                //将每一位替换成26个小写字母
                for (int j=0;j<wordLen;j++){
                    //记录当前字符,之后会恢复成当前字符
                    char origin=charArray[j];
                    for (char c='a';c<='z';c++){
                        charArray[j]=c;
                        //将某个字符修改后的单词
                        String nextWord=String.valueOf(charArray);

                        if (steps.containsKey(nextWord)&&steps.get(nextWord)==step){
                            //在from中给nextWord的单词列表中加上currWord
                            from.get(nextWord).add(currWord);
                        }

                        if (!dict.contains(nextWord)){
                            continue;
                        }

                        dict.remove(nextWord);

                        //dict和steps承担了已经访问过的功能
                        queue.offer(nextWord);

                        //维护 from steps found 的定义
                        from.putIfAbsent(nextWord,new HashSet<>());
                        from.get(nextWord).add(currWord);
                        steps.put(nextWord,step);
                        if (nextWord.equals(endWord)){
                            //因为有多条路径可以到达endWord,找到后不能立即退出,只需要设置found=true
                            found=true;
                        }
                    }
                    charArray[j]=origin;
                }
            }
            if (found){
                break;
            }
        }
        return found;
    }

    private void dfs(Map<String, Set<String>> from, Deque<String> path, String beginWord, String cur, List<List<String>> res) {
        if (cur.equals(beginWord)){
            res.add(new ArrayList<>(path));
            return;
        }
        for (String precursor: from.get(cur)){
            path.addFirst(precursor);
            dfs(from,path,beginWord,precursor,res);
            path.removeFirst();
        }
    }

}

4.练习

（1）被围绕的区域(130)

给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ ，找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

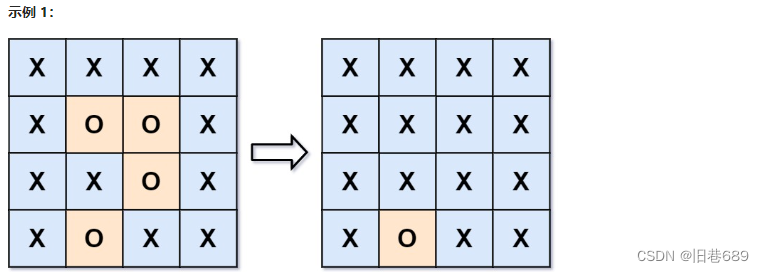
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，
或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

由题可知，任何不在边界上的'Q'，或不与边界上的'Q'相连的'Q'最终都会被填充为'X'。如果两个元素在水平或垂直方向相连，
则称他们是相连的。
所以我们可以找出边界上的'Q'以及和它们相连的'Q'，将它们标记为'1'。然后再遍历整个矩阵，将没有标记的区域全部改为
'X'，将标记了的地方改为'Q'。采用深度优先遍历。

public class test {

    public static void main(String[] args) {
        char[][] chars={{'X','X','X','X'},
                        {'X','O','O','X'},
                        {'X','X','O','X'},
                        {'X','O','X','X'}};
        test t=new test();
        t.solve(chars);
        System.out.print("{");
        for (int i=0;i<chars.length;i++){
            System.out.print("{");
            for (int j=0;j<chars[0].length;j++){
                System.out.print(chars[i][j]+" ");
            }
            System.out.print("},");
        }
        System.out.print("}");
    }

    public void solve(char[][] board) {
        int m= board.length;//矩阵的总行数
        int n=board[0].length;//矩阵的总列数
        //遍历第一列和最后一列
        for (int i=0;i<m;i++){
            dfs(0,i,board,m,n);
            dfs(n-1,i,board,m,n);
        }
        //遍历第一行和最后一行
        for (int j=1;j<n-1;j++){
            dfs(j,0,board,m,n);
            dfs(j,m-1,board,m,n);
        }
        for (int i=0;i<m;i++){
            for (int j=0;j<n;j++){
                if (board[i][j]=='1'){
                    board[i][j]='O';
                }else {
                    board[i][j]='X';
                }
            }
        }
    }

    private void dfs(int col, int row, char[][] board, int m, int n) {
        if (row<0||row>=m||col<0||col>=n||board[row][col]!='O'){
            return;
        }
        //将满足不被填充条件的区域标记
        board[row][col]='1';
        //四个方向进行深度优先遍历
        dfs(col-1,row,board,m,n);
        dfs(col+1,row,board,m,n);
        dfs(col,row-1,board,m,n);
        dfs(col,row+1,board,m,n);
    }

}

（2） 二叉树的所有路径(257)

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。

输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

可以依次遍历整棵树的节点，如果遍历到的当前节点是叶子节点，就将这个路径加入路径列表，如果不是叶子节点，就继续递归
遍历他的左右子节点

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}


public class test {

    public static void main(String[] args) {
        TreeNode treeNode=new TreeNode(1,new TreeNode(2,null,new TreeNode(5)),new TreeNode(3));
        test t=new test();
        List<String> list = t.binaryTreePaths(treeNode);
        System.out.println(list);
    }

    public List<String> binaryTreePaths(TreeNode root) {
        //返回的所有路径
        List<String> paths=new ArrayList<>();
        //一条路径
        String path="";
        dfs(root,path,paths);
        return paths;
    }

    private void dfs(TreeNode root, String path, List<String> paths) {
        if (root!=null){
            StringBuffer pa=new StringBuffer(path);
            pa.append(Integer.toString(root.val));
            //当前节点是叶子节点
            if (root.left==null&&root.right==null){
                paths.add(pa.toString());//加入路径列表
            }else {//不是叶子节点继续遍历
                pa.append("->");
                dfs(root.left,pa.toString(),paths);
                dfs(root.right, pa.toString(), paths);
            }
        }
    }

}

（3） 全排列 II(47)

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

因为要返回所有不重复的全排列，我首先想到的是先找出所有的全排列，再去重。这样确实可以过这道题，但是时间复杂度和空间
复杂度有点不忍直视，如下图

public class test {

    public static void main(String[] args) {
        int[] arr={1,1,2};
        test t=new test();
        System.out.println(t.permuteUnique(arr));
    }

    public List<List<Integer>> permuteUnique(int[] nums) {
        //保存所有的全排列
        List<List<Integer>> paths=new ArrayList<>();
        //保存某个排列
        List<Integer> path=new ArrayList<>();
        //表示某个元素是否已经选择过 默认为false
        boolean[] used=new boolean[nums.length];
        dfs(0,used,path,paths,nums);
        //将得到的集合放入set集合,去重
        Set<List<Integer>> res=new HashSet<>(paths);
        //将去重后的set集合转为列表返回
        List<List<Integer>> list=new ArrayList<>(res);
        return list;
    }

    private void dfs(int depth, boolean[] used, List<Integer> path, List<List<Integer>> paths,int[] nums) {
        //递归退出条件
        if (depth== nums.length){
            paths.add(new ArrayList<>(path));
            return;
        }
        //从0开始依次选择每一个元素作为第一个数
        for (int i=0;i< nums.length;i++){
            if (!used[i]){//当前元素没有使用过
                //链表中加入这个元素
                path.add(nums[i]);
                //标记这个元素
                used[i]=true;
                //递归调用
                dfs(depth+1,used,path,paths,nums);
                //回溯
                used[i]=false;
                path.remove(path.size()-1);
            }
        }
    }
}

这道题可以采用回溯+剪枝，在遍历过程中，一边遍历一边检测，在一定会产生重复结果集的地方剪枝。
我们可以在搜索之前对数组进行排序，这样的话一旦发现某个分支搜索下去可能搜索到重复的元素就停止搜索，这样结果集中不会
包含重复列表
下图是剪枝之后的

public class test {

    public static void main(String[] args) {
        int[] arr={1,1,2};
        test t=new test();
        System.out.println(t.permuteUnique(arr));
    }
    public List<List<Integer>> permuteUnique(int[] nums) {
        //保存所有可能的排列
        List<List<Integer>> paths=new ArrayList<>();
        //保存一个排列
        List<Integer> path=new ArrayList<>();
        //排序 剪枝的前提
        Arrays.sort(nums);
        //某个元素是否访问过 默认false
        boolean[] used=new boolean[nums.length];
        //递归求所有可能的排列
        dsf(0,used,path,paths,nums);
        return paths;
    }

    private void dsf(int depth, boolean[] used, List<Integer> path, List<List<Integer>> paths, int[] nums) {
        //递归终止条件,一个排列中包含了数组中所有的元素
        if (depth== nums.length){
            //将这次排列加入所有的排列中
            paths.add(new ArrayList<>(path));
            return;
        }
        //所有元素都尝试放在开头
        for (int i=0;i< nums.length;i++){
            if (!used[i]){//当前元素没有使用过
                //剪枝条件
                //i>0是为了保证nums[i-1]有意义
                //used[i-1]==false是因为nums[i-1]在深度优先遍历的过程中刚刚被撤销,所以就可能出现重复
                if (i>0&&nums[i]==nums[i-1]&&used[i-1]==false){
                    continue;//开始下一次循环
                }
                //将当前元素加入排列中
                path.add(nums[i]);
                //标记当前元素
                used[i]=true;
                //递归遍历
                dsf(depth+1,used,path,paths,nums);
                //回溯
                used[i]=false;
                path.remove(path.size()-1);
            }
        }
    }
}

（4）组合总和 II(40)

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意：解集不能包含重复的组合。

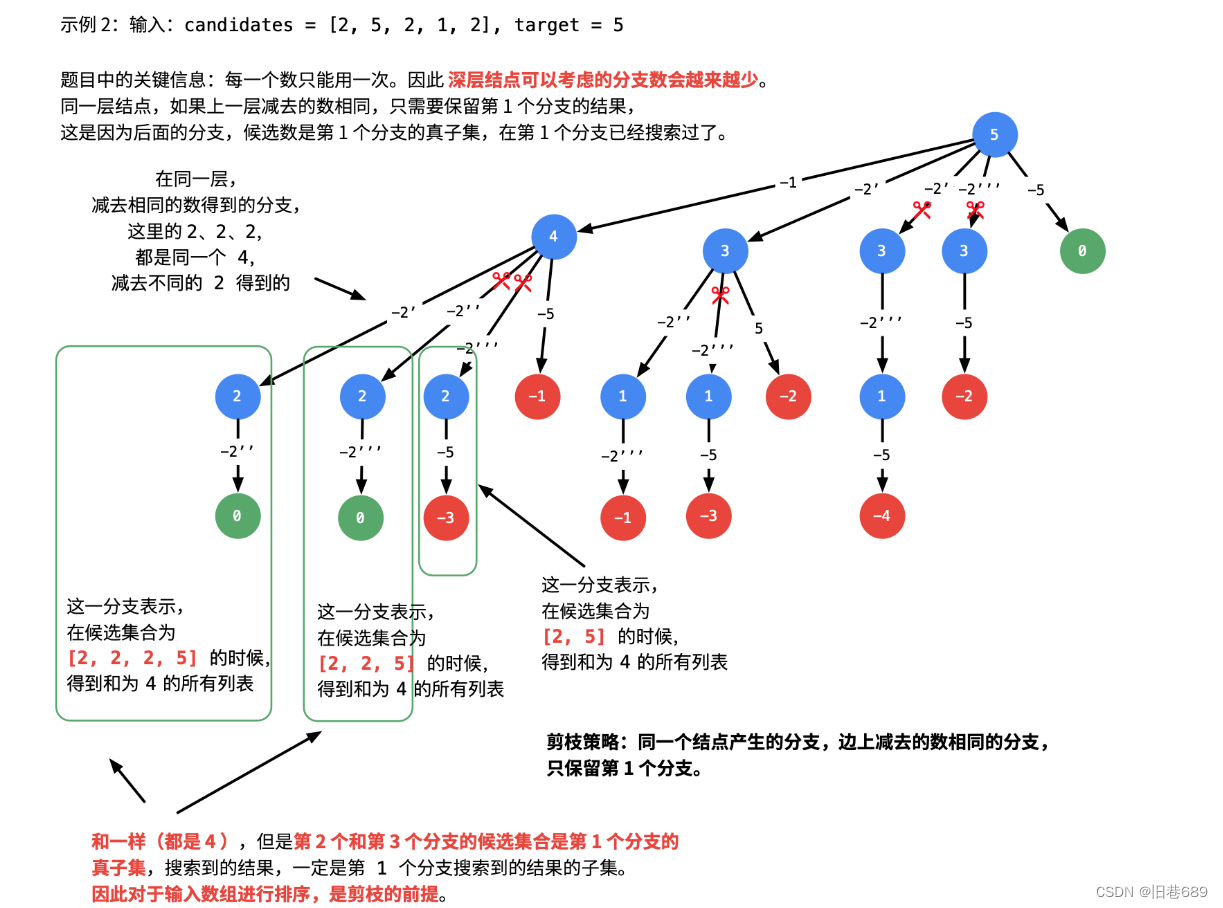
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

要找出所有可以使数字和为target的组合，所以可以考虑深度优先遍历，遍历所有组合中可以满足的组合，输出。
那些恰好使target可以减为0的组合就是满足题意的组合，当某个组合将target减为负数时，那么就可以直接退出了。
将数组排序，若同一层选了多个相同的节点，那么只用第一个节点就可以，其他可以直接剪枝。因为同一层的其他节点，相比于
第一个节点的候选数个数更少，得出的结果集也只是第一个节点的子集

public class test {

    public static void main(String[] args) {
        int[] candidates = new int[]{10, 1, 2, 7, 6, 1, 5};
        int target = 8;
        test t=new test();
        System.out.println(t.combinationSum2(candidates,target));
    }

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        //所有满足题意得组合
        List<List<Integer>> paths=new ArrayList<>();
        //一个组合
        List<Integer> path=new ArrayList<>();
        //将数组排序,这样方便剪枝重复的组合
        Arrays.sort(candidates);
        dfs(0,target,path,paths,candidates);
        return paths;
    }

    private void dfs(int begin, int target, List<Integer> path, List<List<Integer>> paths, int[] candidates) {
        //递归退出条件,当某个组合可以使target为0时,就将它加入paths组合
        if (target==0){
            paths.add(new ArrayList<>(path));
            return;
        }
        //以每一个元素开头,找出可能的组合
        for (int i=begin;i< candidates.length;i++){
            //剪枝:如果减去当前元素小于0,那么就可以直接退出了
            if (target-candidates[i]<0){
                break;
            }
            //剪枝:同一层相同数值的节点,相比于第一个候选数更少而且重复,直接跳过
            if (i>begin&&candidates[i]==candidates[i-1]){
                continue;
            }
            //当前元素加入组合
            path.add(candidates[i]);
            //递归
            dfs(i+1,target-candidates[i],path,paths,candidates);

            path.remove(path.size()-1);
        }
    }

}

（5）解数独(37)

编写一个程序，通过填充空格来解决数独问题。
数独的解法需 遵循如下规则：
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

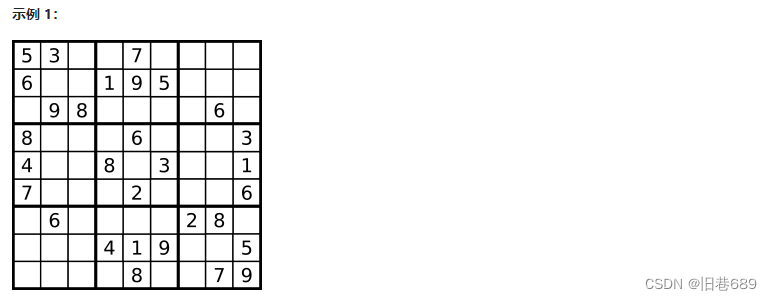
输入：board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]]

输出：[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],
["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],
["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],
["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],
["3","4","5","2","8","6","1","7","9"]]
解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

可以通过递归+回溯的方法枚举所有可能的填法，当递归到最后一个空白格后，如果仍然没有冲突，说明找到了答案；在递归过程中
如果当前空白格不能填下任何一个数字，那么就进行回溯

使用数组记录每个数字是否出现，例如：line[2][3]=true表示数字4在第二行已经出现过了

首先对整个数独数组进行遍历，当我们遍历到第i行j列的位置：
如果该位置是一个空白格，就将其加入一个用来存储空白格位置的列表中，方便后续递归操作
如果该位置是一个数字x，那么我们需要将line[i][x-1],column[j][x-1]以及block[i/3][j/3][x-1]均置为true

当我们开始递归枚举时，当递归到第i行j列的位置，我们枚举填入数字x，line[i][x-1],column[j][x-1]
以及block[i/3][j/3][x-1]必须均为false。当我们填入数字x后，将上述三个值都置为true，并且继续对下一个空白格位置
进行递归。在回溯到当前递归层时，我们还要将上述三个值重新置为false。

public class test {

    private boolean[][] line=new boolean[9][9];
    private boolean[][] column=new boolean[9][9];
    private boolean[][][] block=new boolean[3][3][9];
    private boolean valid=false;
    private List<int[]> spaces=new ArrayList<>();//用来保存空白格的信息

    public static void main(String[] args) {
        char[][] board={{'5','3','.','.','7','.','.','.','.'},
                        {'6','.','.','1','9','5','.','.','.'},
                        {'.','9','8','.','.','.','.','6','.'},
                        {'8','.','.','.','6','.','.','.','3'},
                        {'4','.','.','8','.','3','.','.','1'},
                        {'7','.','.','.','2','.','.','.','6'},
                        {'.','6','.','.','.','.','2','8','.'},
                        {'.','.','.','4','1','9','.','.','5'},
                        {'.','.','.','.','8','.','.','7','9'}};
        test t=new test();
        t.solveSudoku(board);
        for (int i=0;i<9;i++){
            for (int j=0;j<9;j++){
                System.out.print(board[i][j]+" ");
            }
            System.out.println();
        }
    }

    public void solveSudoku(char[][] board) {
        //遍历数独数组
        for (int i=0;i<9;i++){
            for (int j=0;j<9;j++){
                if (board[i][j]=='.'){//如果是空白格,就将信息加入空白格集合
                    spaces.add(new int[]{i,j});
                }else {
                    int digit=board[i][j]-'0'-1;
                    //表示这个数字出现过
                    line[i][digit]=true;
                    column[j][digit]=true;
                    block[i/3][j/3][digit]=true;
                }
            }
        }
        dfs(0,board);
    }

    private void dfs(int pos, char[][] board) {
        //如果当前元素是最后一个空白格,就说明找到了答案
        if (pos== spaces.size()){
            valid=true;
            return;
        }
        int[] space= spaces.get(pos);
        int i=space[0];
        int j=space[1];
        for (int digit=0;digit<9&&!valid;digit++){
            //如果当前数字可以放在这个空白格
            if (!line[i][digit]&&!column[j][digit]&&!block[i/3][j/3][digit]){
                line[i][digit]=true;
                column[j][digit]=true;
                block[i/3][j/3][digit]=true;
                board[i][j]=(char) (digit+'0'+1);
                //递归遍历下一个空白格
                dfs(pos+1,board);
                //回溯
                line[i][digit]=false;
                column[j][digit]=false;
                block[i/3][j/3][digit]=false;
            }
        }
    }
}