Ⅰ. unordered 系列关联式容器

在C++98中，STL提供了底层为红黑树结构的一系列关联式容器，在查询时效率可达到 $log_2 n$ ，即最差情况下需要比较红黑树的高度次，当树中的节点非常多时，查询效率也不理想。最好的查询是，进行很少的比较次数就能够将元素找到，因此在C++11中，STL又提供了4个unordered 系列的关联式容器，这四个容器与红黑树结构的关联式容器使用方式基本类似，只是其底层结构不同，本文中只对unordered_map 进行介绍，unordered_set、unordered_multimap 和 unordered_multiset 可查看文档介绍。

Ⅱ. unordered_map 的使用

1、文档介绍

unordered_map在线文档说明

unordered_map是存储 <key, value> 键值对的关联式容器，其允许通过 key 快速的索引到与其对应的 value。
在 unordered_map 中，键值通常用于惟一地标识元素，而映射值是一个对象，其内容与此键关联。键和映射值的类型可能不同。
在内部,unordered_map 没有对 <key, value> 按照任何特定的顺序排序, 为了能在常数范围内找到 key 所对应的 value，unordered_map 将相同哈希值的键值对放在相同的桶中。
unordered_map 容器通过 key 访问单个元素要比 map 快，但它通常在遍历元素子集的范围迭代方面效率较低。
unordered_map 实现了直接访问操作符(operator[])，它允许使用key作为参数直接访问value。
它的迭代器至少是前向迭代器（也就是单向迭代器）。

2、unordered_map 的接口说明

①容量

函数声明	功能介绍
bool empty() const	检测 unordered_map 是否为空
size_t size() const	获取 unordered_map 的有效元素个数

②unordered_map 的迭代器(无反向迭代器)

函数声明	功能介绍
begin()	返回 unordered_map 第一个元素的迭代器
end()	返回 unordered_map 最后一个元素下一个位置的迭代器
cbegin()	返回 unordered_map 第一个元素的 const 迭代器
cend()	返回 unordered_map 最后一个元素下一个位置的 const 迭代器

③unordered_map 的元素访问

函数声明	功能介绍
operator[]	返回与 key 对应的 value 的引用

🏖 注意：该函数中实际调用哈希桶的插入操作，用参数 key 与 V() 构造一个默认值往底层哈希桶中插入，如果 key 不在哈希桶中，插入成功，返回 V()，插入失败，说明 key 已经在哈希桶中，将 key 对应的 value 返回。

④unordered_map 的查询

函数声明	功能介绍
iterator find(const K& key)	返回 key 在哈希桶中的位置
size_t count(const K& key)	返回哈希桶中关键码为 key 的键值对的个数

🏗 **注意：**unordered_map 中 key 是不能重复的，因此 count 函数的返回值最大为1。

⑤unordered_map 的修改操作

函数声明	功能介绍
insert	向容器中插入键值对
erase	删除容器中的键值对
void clear()	清空容器中有效元素个数
void swap(unordered_map&)	交换两个容器中的元素

⑥unordered_map 的桶操作

函数声明	功能介绍
size_t bucket_count() const	返回哈希桶中桶的总个数
size_t bucket_size(size_t n) const	返回 n 号桶中有效元素的总个数
size_t bucket(const K& key)	返回元素 key 所在的桶号

3、map 和 unordered_map 的区别（set 与 unordered_set 也是）

map 是支持双向迭代器，且迭代的结果是有序的；而 unordered_map 是单向迭代器，且迭代的结果是无序的。
map 的底层是红黑树，而 unordered_map 的底层是哈希表。
如果数据是无序的，采用 unordered_map 效率高；如果数据是有序的，采用 map 的效率更高

Ⅲ. 哈希结构

unordered 系列的关联式容器之所以效率比较高，是因为其底层使用了哈希结构。

1、哈希的概念

顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素时，必须要经过关键码的多次比较。顺序查找时间复杂度为 O(N) **，平衡树中为树的高度，即 O( $log_2 n$ )，搜索的效率取决于搜索过程中元素的比较次数。

理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。 如果构造一种存储结构，通过某种函数 (hashFunc) 使元素的存储位置与它的关键码之间能够建立一一映射的关系，那么在查找时通过该函数可以很快找到该元素。

当向该结构中：

插入元素
- 根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放
搜索元素
- 对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功

该方式即为哈希(散列)方法，哈希方法中使用的转换函数称为哈希 ( 散列 ) 函数，构造出来的结构称为哈希表(Hash Table)( 或者称散列表 )

例如：数据集合{1，7，6，4，5，9}；

哈希函数设置为：hash(key) = key % capacity （capacity为存储元素底层空间总的大小）

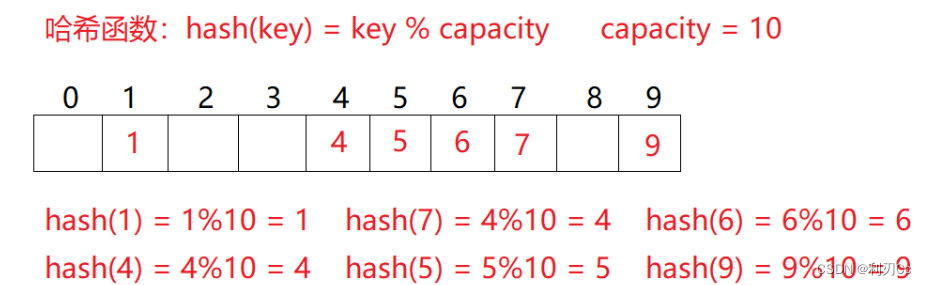
用该方法进行搜索不必进行多次关键码的比较，因此搜索的速度比较快 问题：按照上述哈希方式，向集合中插入元素44，会出现什么问题？答案是发生哈希冲突（或哈希碰撞）！

2、哈希冲突

🏗 不同关键字通过相同哈希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。

把具有不同关键码而具有相同哈希地址的数据元素称为 “ 同义词 ”。

❓ 发生哈希冲突该如何处理呢？哈希冲突可以被解决吗？

💡 答案是 哈希冲突是无法被完全解决的，就像生活中无法完全解决一些矛盾一样，但是如果我们的处理方法越好，那么产生的矛盾也就是哈希冲突就会越少！

下面在介绍解决哈希冲突的方法之前，先介绍一下哈希函数！

3、哈希函数

引起哈希冲突的一个原因可能是：哈希函数设计不够合理。 哈希函数设计原则：

哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有 m 个地址时，其值域必须在 0 到 m-1 之间
哈希函数计算出来的地址能均匀分布在整个空间中
哈希函数应该比较简单

哈希函数作用：建立元素与其存储位置之前的对应关系的，在存储元素时，先通过哈希函数计算元素在哈希表格中的存储位置，然后存储元素。好的哈希函数可以减少冲突的概率，但是不能够绝对避免，万一发生哈希冲突，得需要借助哈希冲突处理方法来解决。

📧 常见哈希函数

直接定制法–(常用)

取关键字的某个线性函数为散列地址： Hash （ Key ） = A*Key + B 优点：简单、均匀缺点：需要事先知道关键字的分布情况使用场景：适合查找比较小且连续的情况 （基数排序的思想就是直接定制法）

除留余数法–(常用)

设散列表中允许的地址数为 m ，取一个不大于 m ，但最接近或者等于 m 的质数 p 作为除数，按照哈希函数： Hash(key) = key% p(p<=m), 将关键码转换成哈希地址
后面我们还会利用BKDR的方法对除留余数法进行优化一下！

平方取中法–(了解)

假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址 平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况

折叠法–(了解)

折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况

随机数法–(了解)

选择一个随机函数，取关键字的随机函数值为它的哈希地址，即 H(key) = random(key),其中 random 为随机数函数。通常应用于关键字长度不等时采用此法

数学分析法–(了解)

设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各位上出现的频率不一定相同，可能在某些位上分布比较均匀，每种符号出现的机会均等，在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小，选择其中各种符号分布均匀的若干位作为散列地址。例如：

假设要存储某家公司员工登记表，如果用手机号作为关键字，那么极有可能前7位都是相同的，那么我们可以选择后面的四位作为散列地址，如果这样的抽取工作还容易出现冲突，还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改成12+34=46)等方法。数字分析法通常适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布较均匀的情况

♻️ 还有其他的方法，比如如果存的是整数的话，那么根据32位比特位来进行存储：可以将这个整数的比特位分出来，如分为四个8位，那么我们可以建立四个数组，每个数组里面放8位比特位的大小也就是 0-255，然后每次查找该整数的时候，先去找该整数的前8位比特位，根据映射去数组中查找，然后后面的三个8位也是一样的，那么总共分下来只需要查找4次，并且非常省空间（分成几组这个是由自己决定的，不同的分组的效果是不一样的，查找的次数也不同）！

💡 注意：哈希函数设计的越精妙，产生哈希冲突的可能性就越低，但是无法避免哈希冲突

Ⅳ. 哈希冲突的解决

解决哈希冲突两种常见的方法是：闭散列和开散列

我们先把闭散列哈希表的框架搭起来！

// 哈希表每个空间给个标记
// EMPTY此位置空， EXIST此位置已经有元素， DELETE元素已经删除
enum Status
{
    EXIST,
    EMPTY,
    DELETE
};

template<class K, class V>
struct HashData
{
    pair<K, V> _kv;
    Status _status = EMPTY; // 这里注意要给默认缺省值初始化，因为这里没有写构造函数，所以不会对枚举类型初始化
};

template<class K, class V>
class hashtable
{
public:
    bool insert(const pair<K, V>& kv);

    void _CheckCapacity();

    HashData<K, V>* find(const K& key);

    bool erase(const K& key);
    
private:
    vector<HashData<K, V>> _tables;
    size_t _n; // 有效数据个数
};

🏗 注：下面在实现闭散列的时候，我们先不会引入哈希函数，等到实现完闭散列后在指出问题的时候再用哈希函数进行问题处理！

1、闭散列

闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把 key 存放到冲突位置中的 “ 下一个 ” **空位置中去。**那如何寻找下一个空位置呢？

① 线性探测

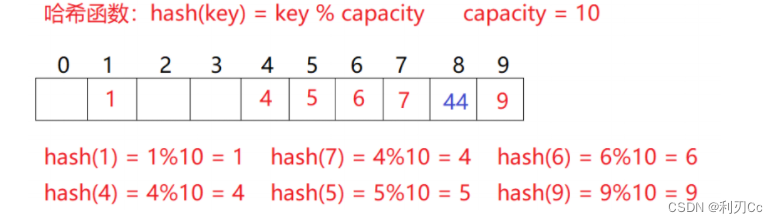
比如一下场景，现在需要插入元素44，先通过哈希函数计算哈希地址，hashAddr为4，因此44理论上应该插在该位置，但是该位置已经放了值为4的元素，即发生哈希冲突。

线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。

插入

先查找一下是否存在重复的元素，是的话直接返回false
然后判断一下容量和负载因子，看看需不需要扩容（下面会讲）
通过哈希函数（这里采用除留余数法）获取待插入元素在哈希表中的位置
如果该位置中没有元素则直接插入新元素，如果该位置中有元素发生哈希冲突，使用线性探测找到下一个空位置，插入新元素

bool insert(const pair<K, V>& kv)
{
    // 进来先判断是否存在重复的元素
    HashData<K, V>* ret = find(kv.first);
    if (ret != nullptr)
		return false;

    // 每次判断是否需要扩容（这个下面会讲）
    _CheckCapacity();

    // 采用除留余数法
    size_t start = kv.first % _tables.size(); 
    size_t i = 0;
    size_t index = start; // 这里多定义一个index是为了等会的二次探测的代码兼容性

    // 线性探测
    while (_tables[index]._status == EXIST)
    {
        i++;
        index = start + i;
        index %= _tables.size(); // 记得取模哈希表的长度，防止越界出去
    }

    // 插入新元素
    _tables[index]._kv = kv;
    _tables[index]._status = EXIST;
    _n++;

    return true;
}

删除
- 采用闭散列处理哈希冲突时，不能随便物理删除哈希表中已有的元素，若直接删除元素会影响其他元素的搜索。比如删除元素4，如果直接删除掉，44查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。简单点说，就是改变要删除元素的 _status 为 DELETE 即可！
```
bool erase(const K& key)
{
    HashData<K, V>* ret = find(key);
    if (ret == nullptr)
    {
        return false;
    }
    else
    {
        --_n;
        ret->_status = DELETE; // 直接改状态即可
        return true;
    }
}
```
查找
- 查找其实就是按插入时候使用的探测方式进行查找。
- 要注意的是查找的条件不只是 _tables[index]._kv.first == key，还得加个 _tables[index]._status == EXIST，因为有可能该点元素的是不算入有效数据的，且数据的状态是 DELETE，所以不加这个条件的话，就会将 DELETE 的节点也算入，所以我们得加入该条件，防止删除作用失效！

HashData<K, V>* find(const K& key)
{
    if (_tables.size() == 0)
        return nullptr;

    // 按insert的监测方式查找
    size_t start = key % _tables.size();
    size_t i = 0;
    size_t index = start + i;
    while (_tables[index]._status != EMPTY)
    {
        // 这里必须加_status == EXIST，因为不加的话在删除后还是能查到该值
        if (_tables[index]._kv.first == key && _tables[index]._status == EXIST)
            return &_tables[index];

        i++;
        //index = start + i * i;  // 这是二次探测
        index = start + i;
        index %= _tables.size();
    }
    // 没找到则返回空
    return nullptr;
}

线性探测优点：实现简单，

线性探测缺点：一旦发生哈希冲突，所有的冲突连在一起，容易产生数据 “ 堆积 ” ，即：不同关键码占据了可利用的空位置，使得寻找某关键码的位置需要许多次比较，导致搜索效率降低。如何缓解呢？就是通过二次探测！不过我们先介绍一下扩容的机制：

❓ 思考：哈希表什么时候扩容？如何扩容？

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wHyXqvaC-1671588684297)(../../img/image-20220916231601979.png)]

总结：在闭散列的线性探测中，0.7是负载因子区分冲突和元素个数的最优分水岭！而我们后面讲的闭散列的二次探测的话，0.5的负载因子是最好的分水岭！

🌵 注意事项：为什么在实现的时候扩容函数的时候不直接调用 vector 的扩容函数呢？
因为 vector 的扩容函数如 resize()，不管是在原地扩容还是异地扩容，它最后都只是将数据拷贝过去，如下图：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Rcel9pJC-1671588684298)(../../img/image-20220916232914743.png)]

但是其实我们需要的效果不是这样子的，我们需要的是这样子的：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nWZuHkg0-1671588684298)(../../img/image-20220916233437741.png)]

所以我们这里可以 定义一个新的哈希表 newTables，然后遍历原表，将原表中的数据按 newSize 映射到新表中去（调用哈希表自己的insert）

void _CheckCapacity()
{
    // 当表的大小为0 或者 负载因子超过0.7 则扩容

    // 负载因子越小，冲突的概率越小，效率越高，但是空间浪费就太大
    // 负载因子越大，冲突的概率越大，效率就越低，但是空间浪费就比较小
    if (_tables.size() == 0 || (_n * 10) / _tables.size() > 7)
    {
        // 扩容
        size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
        hashtable<K, V> newTables;
		newTables._tables.resize(newSize);

        // 这里不能直接调用vector的扩容函数，因为扩容后我们需要对表里的数据重新定位
        // 方法：遍历原表，把原表中的数据，重新按newSize映射到新表
        for (size_t i = 0; i < _tables.size(); ++i)
        {
            if (_tables[i]._status == EXIST)
                newTables.insert(_tables[i]._kv);
        }

        // 最后交换新表和旧表的内容
        _tables.swap(newTables._tables);
    }
}

② 二次探测

线性探测的缺陷是产生冲突的数据堆积在一块，这与其找下一个空位置有关系，因为找空位置的方式就是挨着往后逐个去找，因此二次探测为了避免该问题，找下一个空位置的方法为： $H_i$ = ( $H_0 + i^2$ ) % m, 或者： $H_i$ = ( $H_0 - i^2$ ) % m 。其中： i = 1,2,3… ，是通过散列函数 Hash(x) 对元素的关键码 key 进行计算得到的位置， m 是表的大小。 对于2.1中如果要插入44，产生冲突，使用解决后的情况为：

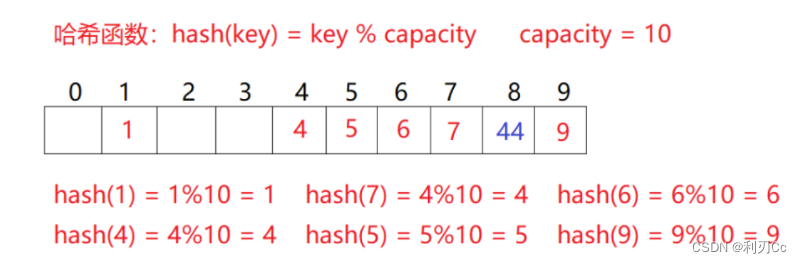
简单的说，就是将线性探测中 i 的次数改为二次

这里以插入为例，其实就是改了一行的代码：

bool insert(const pair<K, V>& kv)
{
    HashData<K, V>* ret = find(kv.first);
    if (ret != nullptr)
        return false;

    _CheckCapacity();

    size_t start = kv.first % _tables.size(); 
    size_t i = 0;
    size_t index = start; // 这里多定义一个index是为了等会的二次探测的代码兼容性

    // 二次探测
    while (_tables[index]._status == EXIST)
    {
        i++;

        index = start + i * i; //只需要改动这行即可！
        //index = start + i;  这个是线性探测

        index %= _tables.size(); // 记得取模哈希表的长度，防止越界出去
    }

    _tables[index]._kv = kv;
    _tables[index]._status = EXIST;
    _n++;

    return true;
}

研究表明：当表的长度为质数且表装载因子 a 不超过 0.5 时，新的表项一定能够插入，而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置，就不会存在表满的问题。在搜索时可以不考虑表装满的情况，但在插入时必须确保表的装载因子 a 不超过 0.5 **，**如果超出必须考虑增容。

🌓 因此：闭散列最大的缺陷就是空间利用率比较低，这也是哈希的缺陷。

这就引入了一个新问题：参数类型问题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QAOUSfU0-1671588684298)(../../img/image-20220917002128702.png)]

这是什么情况？为什么会出现这种情况？我们看看下面的代码就明白了：

void Myhash1()
{
    // 这里我们把闭散列的哈希表放在了命名空间CloseHash中，所以要指定一下
	CloseHash::hashtable<string, string> hs;
	hs.insert(make_pair("liren", "利刃"));
}

可以发现，我们上面的代码中存的 Key 是整形的时候是没问题的，但是如果是 string 呢？如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-awAq8fMk-1671588684299)(../../img/image-20220917003109483.png)]

对吧，这里出现了bug，我们就得实现让所有类型都能通用的方法！

💡 方法：通过哈希函数解决！ 还记得我们上面讲的哈希函数吗，上面没有细讲如何在这里体现，这里它的价值就开始体现出来了！

并且我们之前不是说有优化的方法吗，现在先来看一下一些大佬是怎么做到优化的！

各种字符串Hash函数

上面贴的链接里面就是各种不同的哈希函数算法，这里我们使用BKDR的算法（数据表示BKDR是排名靠前的哈希函数算法）：

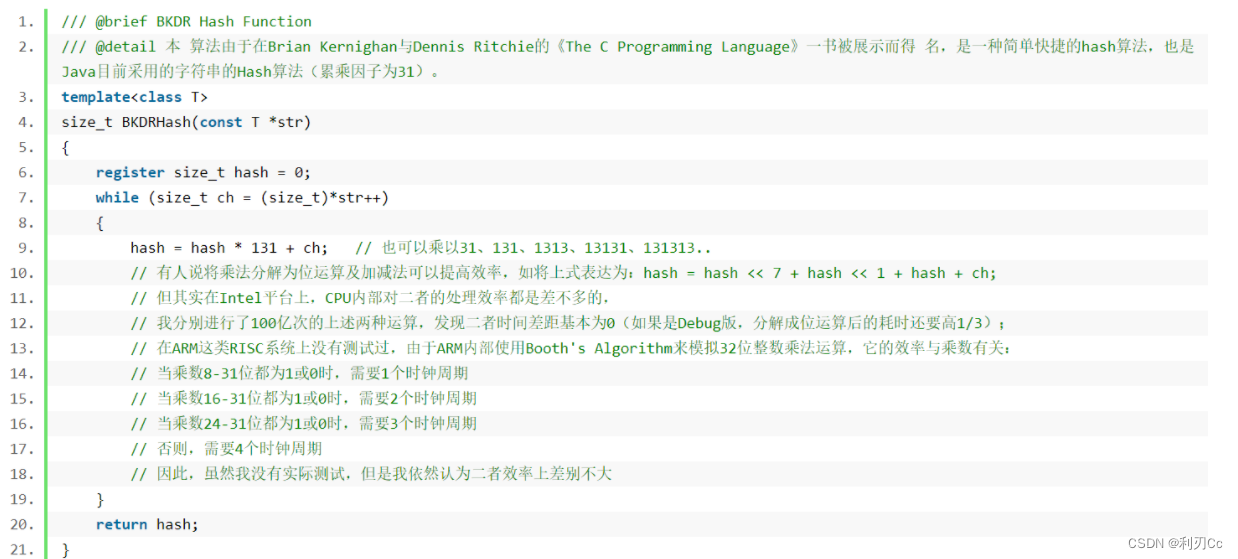
🔺 注意：这里的 BKDR算法还是其他的算法都好，都是为了避免字符串或者字符的哈希冲突问题，因为字符串的长度是不定的，而且就算不同长度的字符串，ASCII码值也可能是一样的，所以才采用这些哈希函数算法来尽量避免哈希冲突问题！

template <class K>
struct hash
{
    // 对于普通的类型，直接返回key即可
    size_t operator()(const K& key)
    {
        return key;
    }
};

// 特化
template<>
struct hash<string>
{
    size_t operator()(const string& s)
    {
        // 采用BKDR算法
        size_t value = 0;
        for (auto ch : s)
        {
            value *= 31;
            value += ch;
        }
        return value;
    }
};

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-voVGWIpN-1671588684299)(../../img/image-20220917100726100.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MUsPvvOW-1671588684299)(../../img/image-20220917100845637.png)]

并且这里我们运用的是模板的特化！

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KN2lhqk6-1671588684299)(../../img/image-20220917101119481.png)]

🐛 这样子我们就得去 insert 和 find 函数里面去添加一些小细节也就是哈希函数啦：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-64k3upOy-1671588684300)(../../img/image-20220917105119408.png)]

❓ 问题：为什么上面哈希函数中的返回值都是 size_t 而不能是 int 呢？

💡 解答： 因为如果我们传过去的是一个负数比如 tmp.insert(make_pair(-999, 199)); 要知道负数也是可以取模的，但是结果是个负数，那么当我们后面在访问的时候，访问了负数下标位置的元素，那么就是越界访问了，所以这里我们返回值传的就是 size_t 比较合理！

🔺 纠错：上面图片中的insert的第二行判断时候是 if ( ret != nullptr ) 才对

2、开散列

① 开散列的概念

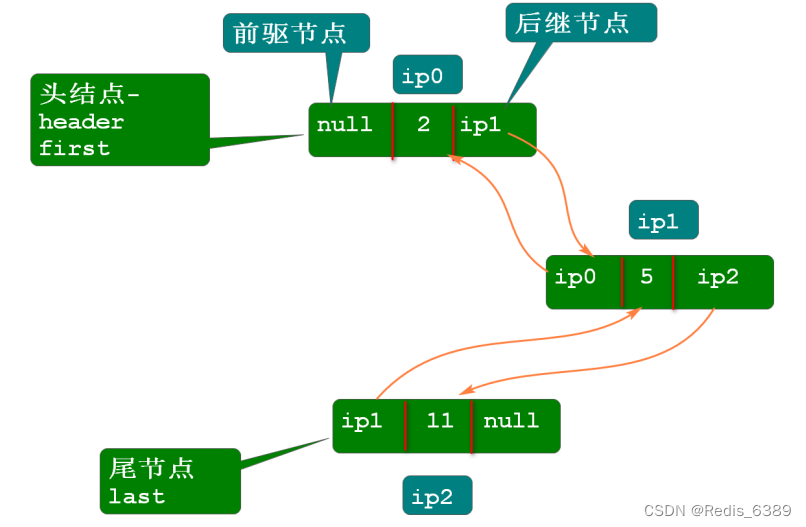
开散列法又叫链地址法 ( 开链法、拉链法、哈希桶 ) ，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

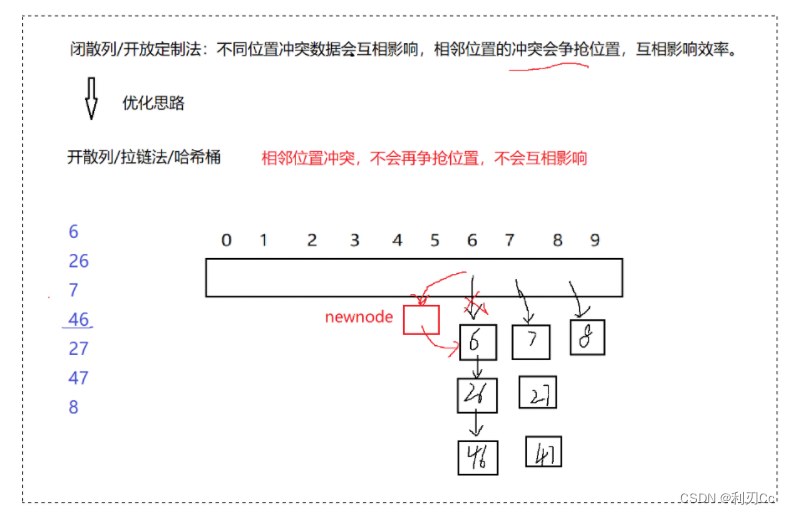
从上图可以看出，开散列中每个桶中放的都是发生哈希冲突的元素。

🚗 开散列的框架如下：

namespace LinkHash
{
	template <class K, class V>
	struct HashNode
	{
		pair<K, V> _kv;
		HashNode<K, V>* _next;

		HashNode(const pair<K, V>& kv, HashNode<K, V>* next = nullptr)
			:_kv(kv)
			, _next(next)
		{}
	};

	template <class K, class V, class HashFunc = Hash<K>>
	class hashtable
	{
		typedef HashNode<K, V> Node;
	public:
		bool insert(const pair<K, V>& kv);

		void _CheckCapacity();
        
		Node* find(const K& key);
		
		bool erase(const K& key);
        
	private:
		vector<Node*> _tables; // 指针数组
		size_t _n = 0; // 有效数据个数
	};
}

② 开散列的操作

插入
1. 首先检查一下是否有重复的元素，有的话返回false
2. 然后检查一下是否需要扩容（与闭散列不一样，等会会讲）
3. 进行插入操作（与闭散列不同）：
  - 就相当于单链表中的插入嘛，但是这里要注意的是，如果我们选择的是尾插，那么我们就得遍历一遍链表，那么效率就低了，没什么意义！所以我们选择的是头插！
4. 最后将有效个数 _n++ 即可

bool insert(const pair<K, V>& kv)
{
    // 检测是否有重复元素
    Node* ret = find(kv.first);
    if (ret != nullptr)
        return false;

    // 检测是否需要扩容
    _CheckCapacity();

    HashFunc _hs; // 哈希函数
    size_t index = _hs(kv.first) % _tables.size();
    Node* newnode = new Node(kv);

    // 头插
    newnode->_next = _tables[index];
    _tables[index] = newnode;
    ++_n;

    return true;
}

删除
1. 首先判断一下该元素是否存在，不存在则直接返回false
2. 接着就是删除操作，由于我们实现的是单链表，所以这里其实不太方便，但是我们可以在查找该元素的同时，标记一个 prev 用于标记该元素的上一个位置，且 prev 初始化为 nullptr，然后就会有以下的情况：
  - 若 prev 为 nullptr，则说明当前位置最多只有一个元素，那么这相当于是单链表中的头删
  - 若 prev 不为 nullptr，则说明当前位置有多个元素，则相当于单链表中的任意位置删除
3. 处理完后记得将有效个数 _n–

bool erase(const K& key)
{
    if (_tables.size() == 0)
        return false;

    HashFunc _hs; // 哈希函数

    size_t index = _hs(key) % _tables.size();
    Node* pre = nullptr;
    Node* cur = _tables[index];
    while (cur != nullptr)
    {
        if (cur->_kv.first != key)
        {
            pre = cur;
            cur = cur->_next;
        }
        else
        {
            // 找到了开始删除
            if (pre == nullptr) // 头删
            {
                _tables[index] = cur->_next;
            }
            else // 中间删
            {
                pre->_next = cur->_next;
            }
            delete cur;
            // 记得减少有效个数
            --_n;

            return true;
        }
    }
    // 没找到直接返回false
    return false;
}

查找
- 查找比较简单，其实就是遍历单链表
- 若找不到则返回 nullptr 即可

Node* find(const K& key)
{
    if (_tables.size() == 0)
        return nullptr;

    HashFunc _hs; // 哈希函数

    size_t index = _hs(key) % _tables.size();
    Node* cur = _tables[index];
    while (cur != nullptr)
    {
        if (cur->_kv.first == key)
            return cur;
        cur = cur->_next;
    }
    return nullptr;
}

③ 开散列的扩容

桶的个数是一定的，随着元素的不断插入，每个桶中元素的个数不断增多，极端情况下，可能会导致一个桶中链表节点非常多，会影响哈希表的性能，因此在一定条件下需要对哈希表进行增容，那该条件怎么确认呢？开散列最好的情况是：每个哈希桶中刚好挂一个节点，再继续插入元素时，每一次都会发生哈希冲突，因此，在元素个数刚好等于桶的个数时，可以给哈希表增容。

🔺 注意事项：与闭散列一样，开散列的扩容也不能直接对其底层的 vector 直接使用 resize 等扩容函数，因为我们希望的是扩容后，一些桶里的数据又被均摊到别的桶中去，所以我们这里重新开辟一个 vecotr 变量，然后我们遍历原来的 vector，将其元素按 newSize 插入到新的 vector 中！

void _CheckCapacity()
{
    // 当表为空或者负载因子为1的时候扩容
    if (_tables.size() == 0 || _n == _tables.size())
    {
        // 与闭散列不同，开散列这里不推荐新建一个哈希表进行插入，而是直接新建一个vector插入即可
        size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
        vector<Node*> newTables(newSize);

        HashFunc _hs; // 哈希函数

        for (size_t i = 0; i < _tables.size(); ++i)
        {
            Node* cur = _tables[i];

            // 重新头插到newTables
            while (cur != nullptr)
            {
                Node* next = cur->_next;

                // 头插
                size_t index = _hs(cur->_kv.first) % newTables.size();
                cur->_next = newTables[index];
                newTables[index] = cur;

                // 继续往下循环遍历单链表
                cur = next;
            }

            // 保险起见，将旧表_tables的指针变成空指针
            _tables[i] = nullptr;
        }
        _tables.swap(newTables);
    }
}

3、关于扩容的选择（素数）

除留余数法，最好模一个素数，为什么？如何每次快速取一个类似两倍关系的素数？

💡 唯一的原因是 避免将值聚类到少量存储桶中，分布更均匀的哈希表将更一致地执行。

🚅 通过一个素数表，我们每次取下一个两倍左右大小的素数即可！

// 获取下一个素数
size_t GetNextPrime(size_t prime)
{
    const int PrimeCount = 28;
    static const size_t primeList[PrimeCount] =
    {
        53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,
        49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917,
        25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291
    };

    size_t i = 0;
    for (i = 0; i < PrimeCount; ++i)
    {
        if (primeList[i] > prime)
            return primeList[i];
    }

    return primeList[i];
}

然后将 _CheckCapacity() 中的 newSize 改一下即可！

size_t newSize = GetNextPrime(_tables.size());

Ⅴ. 闭散列和开散列的比较

应用链地址法处理溢出，需要增设链接指针，似乎增加了存储开销。事实上： 由于开地址法必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子 a <= 0.7 ，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间。

Ⅵ. 哈希表的完整代码

#pragma once
#include <iostream>
#include <string>
#include <vector>
using namespace std;

template <class K>
struct Hash
{
	size_t operator()(const K& key)
	{
		return key;
	}
};

// 特化
template<>
struct Hash <string>
{
	size_t operator()(const string& s)
	{
		// BKDR
		size_t value = 0;
		for (auto ch : s)
		{
			value *= 31;
			value += ch;
		}
		return value;
	}
};

namespace CloseHash
{
	enum Status
	{
		EXIST,
		EMPTY,
		DELETE
	};

	template <class K, class V>
	struct HashData
	{
		pair<K, V> _kv;
		Status _status = EMPTY;
	};

	template <class K, class V, class HashFunc = Hash<K>>
	class hashtable
	{
	public:
		bool insert(const pair<K, V>& kv)
		{
			// 进来先判断是否存在重复的元素
			HashData<K, V>* ret = find(kv.first);
			if (ret)
				return false;

			// 每次判断是否需要扩容
			_CheckCapacity();

			HashFunc _hs; //哈希函数

			// 采用除留余数法
			size_t start = _hs(kv.first) % _tables.size();
			size_t i = 0;
			size_t index = start; // 这里多定义一个index是为了等会的二次探测的代码兼容性

			// 线性探测
			while (_tables[index]._status == EXIST)
			{
				i++;

				//index = start + i * i;
				index = start + i;

				index %= _tables.size(); // 记得取模哈希表的长度，防止越界出去
			}

			// 插入新元素
			_tables[index]._kv = kv;
			_tables[index]._status = EXIST;
			_n++;

			return true;
		}

        // 获取下一个素数
		size_t GetNextPrime(size_t prime)
		{
			const int PrimeCount = 28;
			static const size_t primeList[PrimeCount] =
			{
				53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,
				49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917,
				25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 				  4294967291
			};

			size_t i = 0;
			for (i = 0; i < PrimeCount; ++i)
			{
				if (primeList[i] > prime)
					return primeList[i];
			}

			return primeList[i];
		}
        
		void _CheckCapacity()
		{
			// 当表为空或者负载因子为1的时候扩容
			if (_tables.size() == 0 || _n == _tables.size())
			{
				// 与闭散列不同，开散列这里不推荐新建一个哈希表进行插入，而是直接新建一个vector插入即可
				size_t newSize = GetNextPrime(_tables.size());
				vector<Node*> newTables(newSize);

				KeyOfT kt;
				HashFunc _hs; // 哈希函数

				for (size_t i = 0; i < _tables.size(); ++i)
				{
					Node* cur = _tables[i];

					// 重新头插到newTables
					while (cur != nullptr)
					{
						Node* next = cur->_next;

						// 头插
						size_t index = _hs(kt(cur->_data)) % newTables.size();
						cur->_next = newTables[index];
						newTables[index] = cur;

						// 继续往下循环遍历单链表
						cur = next;
					}

					// 保险起见，将旧表_tables的指针变成空指针
					_tables[i] = nullptr;
				}
				_tables.swap(newTables);
			}
		}

		HashData<K, V>* find(const K& key)
		{
			if (_tables.size() == 0)
				return nullptr;

			HashFunc _hs; //哈希函数

			// 按insert的监测方式查找
			size_t start = _hs(key) % _tables.size();
			size_t i = 0;
			size_t index = start + i;
			while (_tables[index]._status != EMPTY)
			{
				// 这里必须加_status == EXIST，因为不加的话在删除后还是能查到该值
				if (_tables[index]._kv.first == key && _tables[index]._status == EXIST)
					return &_tables[index];

				i++;
				//index = start + i * i;
				index = start + i;
				index %= _tables.size();
			}
			// 没找到则返回空
			return nullptr;
		}

		bool erase(const K& key)
		{
			HashData<K, V>* ret = find(key);
			if (ret == nullptr)
			{
				return false;
			}
			else
			{
				--_n;
				ret->_status = DELETE;
				return true;
			}
		}
	private:
		vector<HashData<K, V>> _tables;
		size_t _n = 0; // 有效数据个数
	};
}

namespace LinkHash
{
	template <class K, class V>
	struct HashNode
	{
		pair<K, V> _kv;
		HashNode<K, V>* _next;

		HashNode(const pair<K, V>& kv, HashNode<K, V>* next = nullptr)
			:_kv(kv)
			, _next(next)
		{}
	};

	template <class K, class V, class HashFunc = Hash<K>>
	class hashtable
	{
		typedef HashNode<K, V> Node;
	public:
		bool insert(const pair<K, V>& kv)
		{
			// 检测是否有重复元素
			Node* ret = find(kv.first);
			if (ret != nullptr)
				return false;

			// 检测是否需要扩容
			_CheckCapacity();

			HashFunc _hs; // 哈希函数
			size_t index = _hs(kv.first) % _tables.size();
			Node* newnode = new Node(kv);

			// 头插
			newnode->_next = _tables[index];
			_tables[index] = newnode;
			++_n;

			return true;
		}

		void _CheckCapacity()
		{
			// 当表为空或者负载因子为1的时候扩容
			if (_tables.size() == 0 || _n == _tables.size())
			{
				// 与闭散列不同，开散列这里不推荐新建一个哈希表进行插入，而是直接新建一个vector插入即可
				size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
				vector<Node*> newTables(newSize);

				HashFunc _hs; // 哈希函数

				for (size_t i = 0; i < _tables.size(); ++i)
				{
					Node* cur = _tables[i];

					// 重新头插到newTables
					while (cur != nullptr)
					{
						Node* next = cur->_next;

						// 头插
						size_t index = _hs(cur->_kv.first) % newTables.size();
						cur->_next = newTables[index];
						newTables[index] = cur;

						// 继续往下循环遍历单链表
						cur = next;
					}

					// 保险起见，将旧表_tables的指针变成空指针
					_tables[i] = nullptr;
				}
				_tables.swap(newTables);
			}
		}

		Node* find(const K& key)
		{
			if (_tables.size() == 0)
				return nullptr;

			HashFunc _hs; // 哈希函数

			size_t index = _hs(key) % _tables.size();
			Node* cur = _tables[index];
			while (cur != nullptr)
			{
				if (cur->_kv.first == key)
					return cur;
				cur = cur->_next;
			}
			return nullptr;
		}

		bool erase(const K& key)
		{
			if (_tables.size() == 0)
				return false;

			HashFunc _hs; // 哈希函数

			size_t index = _hs(key) % _tables.size();
			Node* pre = nullptr;
			Node* cur = _tables[index];
			while (cur != nullptr)
			{
				if (cur->_kv.first != key)
				{
					pre = cur;
					cur = cur->_next;
				}
				else
				{
					// 找到了开始删除
					if (pre == nullptr) // 头删
					{
						_tables[index] = cur->_next;
					}
					else // 中间删
					{
						pre->_next = cur->_next;
					}
					delete cur;
					// 记得减少有效个数
					--_n;

					return true;
				}
			}

			// 没找到直接返回false
			return false;
		}
	private:
		vector<Node*> _tables; // 指针数组
		size_t _n = 0; // 有效数据个数
	};
}