《记忆力心理学》
关于作者
赫尔曼•艾宾浩斯,西方心理学泰斗级人物,生活在19世纪的德国心理学家。他是最早用实验的方法对记忆进行量化研究的 人,最受人瞩目的贡献,就是发现了记忆保持曲线。
关于本书
这本书可以看作是记忆心理学的开山之作,它是第一本对记忆的研究记录报告。 书中不仅揭示了记忆的规律,还给出了记忆实验的细节描述,指出了增强记忆力的方法。这本书既是一本揭示记忆奧秘的百科全书,又是一本增强记忆的科普教程。
核心内容
记忆的规律以及增强记忆力的五种方法。
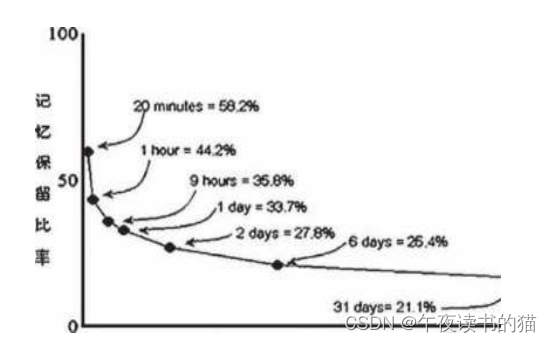
- 记忆力曲线
记忆力曲线是用来描述记忆与遗忘规律的。记忆力曲线的纵轴,代表记忆内容的数量,横轴代表天数,也就是被试在记忆完毕后经历的天数。这条曲线呈现下降的趋势,最开始下降的最快。记忆的遗忘速度是不规则的,不是每天忘掉平均数量的内容,而是在最开始的阶段遗忘得最快, 随着时间的推移,遗忘的速度逐渐放慢, 最后遗忘停止,没有被遗忘的记忆就成为了长期记忆,可以被随时调取,或者在某些特殊环境和某个事件的触发下再次让你想起来。记忆力曲线给予我们的启发就是,在学习一些东西之后,及时复习很重要,在遗忘点出现之前复习,这样就能避免遗忘的出现,把知识变成更多的长期记忆,从而终身保留下来。
二、复习法
提高记忆力的首要方法就是降低遗忘的概率。根据记忆力曲线分析,如果记忆的内容在20分钟后不复习,就会遗忘40%以
上,9个小时后就会遗忘65%左右。
- "351-351"记忆法
这个方法的重点就在于掌握最恰当的复习 间隔。具体做法是,当你把需要学习的内容全部记住后,要尽量在3个小时之内回忆 遍,接下来,分别在5小时内、10小时 内、3天内、5天内、10天内复习一遍,经过 这6次的学习,长期记忆就会形成,你对这 部分内容的记忆会相当深刻。
- 整体复习
我们在复习背诵的文章时,遇到记不起来 的段落不要翻书查看,把这一段略过去, 继续往下回忆,整篇文章已经复习完后, 再重新回想刚才遗忘的那一部分,这时候,我们也许就很容易回忆起那一段遗忘 的内容。这是因为内容上下文之间是有联 系的,如果我们把记忆的整体内容框架把 握好,就可以利用整体将暂时遗忘的部分 重新回忆起来。
- 回忆记忆法
回忆过程所用的时间越多,记忆的效率越高。这里的"回忆",指的是把记住的知识在头脑中再回想一遍。在背诵东西的时候, 我们就需要这种刻意的回忆。比如,在朗读一小段文章后,开始回忆这部分内容, 先通过回忆验证哪些记住了、哪些没有记 住,没有记住的部分再看书背诵。相对于反复的朗读,通过回忆背诵具有更好的效果。
三、 链接记忆法
找到需要记忆的内容和内容之间的链接点,形成一个记忆链条,从而更快地记住 大量的内容。如果遇到不熟悉的或者抽象难理解的内容,就需要把它进行转换,变为生动、直观的形象内容,激发自己的正面情绪,从而更利于记忆。
【案例】
记忆蒸汽机、人、马、面包、神父、酒吧这 几个词,可以用链接的方式把每一组连成 一句话。比如,蒸汽机和人一一人和蒸汽机 比工作速度,结果累得满头大汗;马和面 包一-这匹马很肥,就像一个大面包;神父 和酒吧--神父去酒吧喝酒,醉酒之后大闹 酒吧。用这种链接的方式,我们就将每组 的两个形象词语串联到了一起,组成了有 趣的一句话。
当你需要记住一整本书的时候,词汇量是 非常庞大的,这个时候,你就需要运用环 形的链式记忆法,让彼此没有关联的词汇 环环相扣。
【案例】
记忆绳子、斧头、椅子、耶稣、石榴这五个 词,为了方便记忆,可以把这五个词相互 关联到一起,比如,绳子跟斧头——把斧 头上绑着五颜六色的绳子;斧头和椅子-- 斧头从天上掉下来,把椅子砸了一个洞; 椅子跟耶稣--耶稣坐在一个闪闪发光的 椅子上;耶稣和石榴--耶稣悄悄把石榴藏 到了裤子里。
你甚至可以把自己当做主角,根据这些词 汇编一个故事,把链接升级。因为故事有 情节有意义,能够让人情绪高涨,尤其是 假想自己身上发生的故事,就会记忆更 牢。
四、 联想记忆法
这种方法是利用联想使思维发散,产生画面感。联想的画面越夸张越能让人印象深刻,因为人们通常无法记住每天见到的那 些不起眼的小事,但是对那些古怪的场景 却是印象;米刻。
【案例】
心理学家把击剑爱好者分成三组:第一组 每天练习20分钟的实际击剑,练习20天; 第二组在20天内不做任何练习;第三组在 20天内先做10分钟的实际击剑,再做10分 钟的冥想击剑,也就是靠着想象纠正自己 的技术动作。结果第三组进步率最高。这 个实验就说明,想象力对人的作用是巨大 的。
五、整体浓缩记忆法
整体浓缩的方法,就是把内容看作一个整体,然后再找出重点,通过重点内容的清单,浓缩记忆,串起整个内容。
【案例】
把整篇内容通读一遍,然后分块提炼出有 特点的或者有代表性的句子,比如带有数 字的句子,或者是能够体现文章中心的句 子,把这些句子整合在一起,在需要背诵 的时候,利用这些有特点的内容还原出整 体内容。
金句
- 没有记忆,人类可能还停留在原始 段,无法学会任何高级方式,只能靠本能 重复千篇一律的生活。
- 短期记忆只有转化为长期记忆才能对我 们的生活产生有效的帮助。
- 所谓记忆力强,其实就是一直在跟遗忘抗争。
- 因为故事有情节有意义,能够让人情绪 高涨,尤其是假想自己身上发生的故事, 就会记忆更牢。