算法原理

给出一列数字，在有些情况下，这些数字的值得绝对大小不重要，而相对大小很重要。例如，对一个班级学生的成绩进行排名，此时不关心成绩的绝对值，只需要输出排名，如分数为{95，50，72，21}，排名为{1，3，2，4}。

离散化就是用数字得相对值替代他们得绝对值。离散化是一种数据处理的技巧。

它把分布广而稀疏的数据转换为密集分布,从而能够让算法更快速、更省空间地处理。

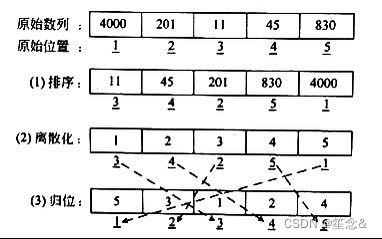
例如，（4000,201,11,45,830),数字的分布很稀疏,按大小排序为(5,3,1,2,4),若算法处理的是数字的相对位置问题,那么对后者的处理更容易。

离散化步骤如下。

1）排序：首先需要对数列排序,排序后才能确定相对大小。

2）离散化：把排序后的数列元素从 1开始逐个分配数值,完成离散化。

3）归位：把离散化后的每个元素放回原始位置,结束。图 2.15 演示了把(4000,201,11,45,830)离散化为(5,3,1,2,4)的过程。带下画线的字记录了原始位置,相当于数据的原始地址,最后的归位需要利用这些下画线数字。

算法模板

1）手工编码

给定得数列中经常有重复的数据，如{4000，201，11，45，11}.数字11重复了，可以分为两种情况进行离散化

1）一般把相同的数据离散化为相同的数据，即把{4000，201，11，45，11}.离散化为{5，4，1，3，1}.

下面是代码，其中olda[]记录原始数据，newa[]是离散化的结果。

#include<stdio.h>
#define N  500010   //自己定义一个范围
struct node{
  int val;              //元素的值
  int id;               //元素的位置
}olda[N]; //离散化之前的原始数据

int newa[N]; //离散化后的结果

int cmp(const void *a,const void *b)
	{ 
	 struct node *aa = (struct node *)a;
     struct node *bb = (struct node *)b;
     return (((aa->val) > (bb->val)));	
	}
	
int main(){
 	int n;      
	scanf("%d",&n);                  //读元素个数
    for(int i=1;i<=n;i++)
	{
        scanf("%d",&olda[i].val);                //读元素的值
        olda[i].id = i;                          //记录元素的位置
	}
	qsort(&olda[1],n,sizeof(olda[1]),cmp);             //对元素的值排序
    for(int i=1;i<=n;i++)
	{                       //生成 newa[]
		newa[olda[i].id]=i; //这个元素原来的位置在olda[i].id，把它的值赋为i，i是离散化后的新值
	    if(olda[i].val == olda[i-1].val)          //若两个元素的原值相同，把新值赋为相同
			newa[olda[i].id] = newa[olda[i-1].id];
    }
    for(int i=1;i<=n;i++)  
	printf("%d ",newa[i]); //打印出来看看
    return 0;
}

2）有时要求后出现的数据比先出现的大，即把{4000，201，11，45，11}.离散化为{5，4，1，3，2}.把上面的代码的倒数第六七行注释即可。

对于c++玩家，若需要对重复的数据进行去重，可以使用unique函数

2）c++用STL函数实现离散化

可以用 STL的 lower bound()和unique函数实现离散化。
lower_bound()函数的功能是在有序的数列中查找某个元素的相对位置。这个位置正好是做离散化时元素初值对应的新值。
有时还需要用 unique()函数去重,下面分别讨论不去重和去重情况下的操作。
(1)不去重,把相同的数据离散化为相同的数据。把(4000,201,11,45,11)离散化为(5,4,1,3,1),代码如下。

#include<bits/stdc++.h>
using namespace std;
const int N = 500010;  // 自己定义一个范围
int olda[N];           // 离散化前
int newa[N];           // 离散化后
int main(){
    int n;    scanf("%d",&n);
    for(int i=1;i<=n;i++) {
        scanf("%d",&olda[i]);      //读元素的值
        newa[i] = olda[i];
	}
    sort(olda+1,olda+1+n);         //排序
    int cnt = n;
  //cnt = unique(olda+1,olda+1+n)-(olda+1);  //去重，cnt是去重后的数量
    for(int i=1;i<=cnt;i++)                  //生成 newa[]
		newa[i]=lower_bound(olda+1,olda+1+n,newa[i])-olda; 
                   //查找相等的元素的位置，这个位置就是离散化后的新值
    for(int i=1;i<=cnt;i++)   printf("%d ",newa[i]);   //打印出来看看        
    printf("\n cnt=%d",cnt);    
    return 0;
}

2）去重，把相同的数据离散化为一个数据，上述代码加上第14行的去重功能后，离散化为{4，3，1，2}