相关阅读

数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482

---

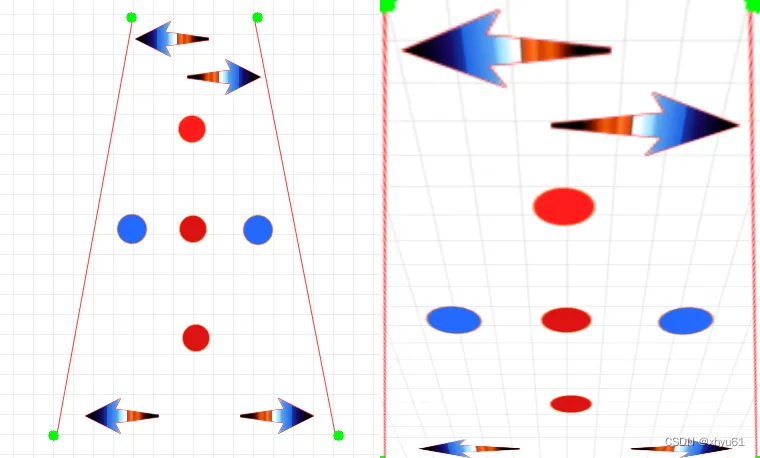
        进位保留乘法器依旧保留着阵列的排列规则，只是进位是沿斜下角，如果能使用树形结构来规划这些进位保留加法器，就能获得更短的关键路径延迟和更小的器件开销，这种结构的乘法器被称为华莱士树乘法器。图1所示为使用四位华莱士树乘法器的例子，图中总共有十六个部分积，分别通过被乘数和乘数的各位相与（通过与门）得到，图中的斜杠/代表一个全加器，连接的分别是右上角的本位和以及左下角给高位的进位，带反斜杠\的/表示是半加器。

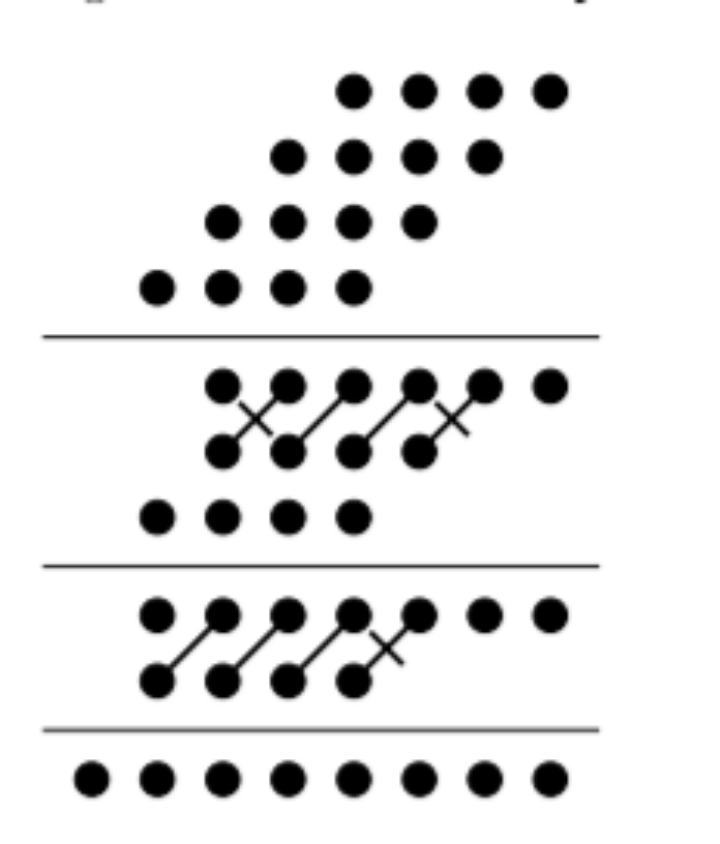
图1 华莱士树乘法器的覆盖过程

        第一阶段华莱士将所有的部分积按行，每三行分组，在组内使用保留进位加法器（有全加器和半加器两种）压缩，当组内某一列含有三个部分积，则使用全加器压缩；若含有两个部分积，则使用半加器压缩，含有一个部分积，则不压缩。分组时的多余行不进行压缩，直接传递到下一阶段（在这里指的是第四行）。       

        下一阶段中，继续三行分一组，进行压缩，直到最后得到两行部分积，此时使用一个普通的多位传播进位加法器或者超前进位加法器等进行（两数相加）向量合并。可以看到只需要两个阶段，十六个部分积就可被压缩至两行。这个结构使用了五个全加器和三个半加器（不包括最后的向量合并器）。 

        具体的Verilog代码实现见附录，Modelsim软件仿真如图2所示。使用Synopsis的综合工具Design Compiler综合的结果如图3所示，综合使用了0.13μm工艺库。

图2 华莱士树乘法器仿真结果

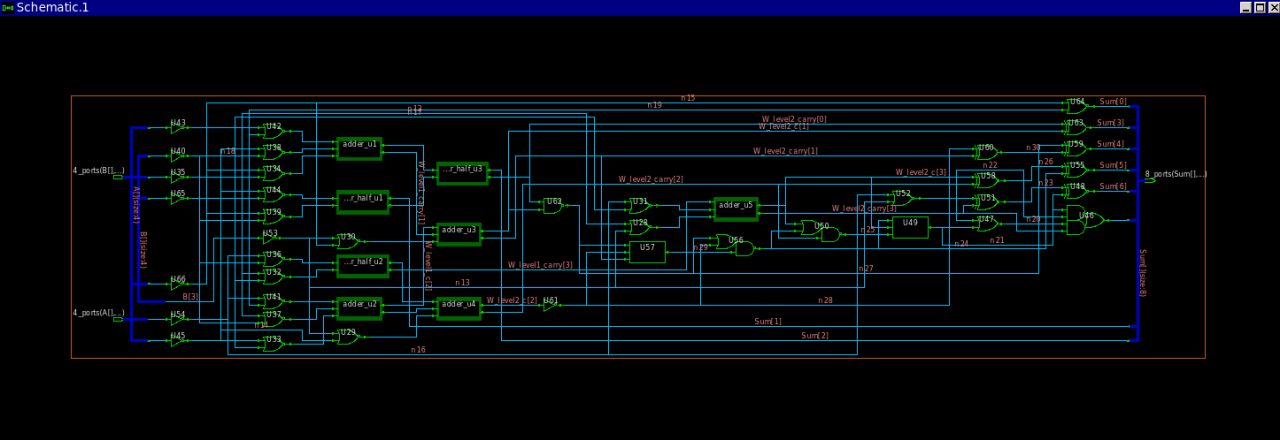图3 华莱士树乘法器综合结果

        在Design Compiler中使用report_timing命令，可以得到关键路径的延迟，如图4所示，可以看出延迟仅有1.39ns。性能优于进位保留乘法器，远由于普通的阵列乘法器，这是由于此时将部分分组并分别处理，结果大约能在三级加法器的延迟后得到。

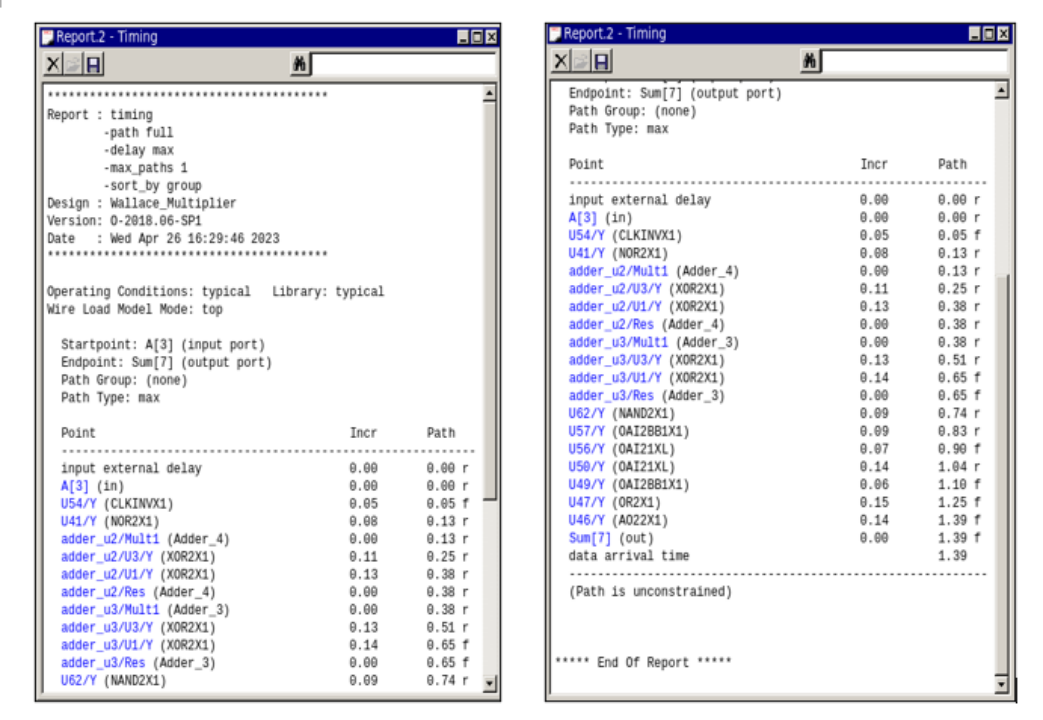图4 华莱士树乘法器关键路径报告

        在Design Compiler中使用report_area命令，报告所设计电路的面积占用情况，如图5所示，可以看到这个面积略大于阵列乘法器，这是由最后的向量合并加法器贡献的，所以这个面积随着数据位宽的增加不会迅速变大。如果不考虑向量合并加法器的影响，阵列乘法器使用了八个全加器和四个半加器，进位保留乘法器使用了六个全加器和六个半加器，而华莱士树乘法器仅仅用了五个全加器和三个半加器，该实现减少了位宽较大乘法器的硬件开销，同时对传播延时的优化也很显著。

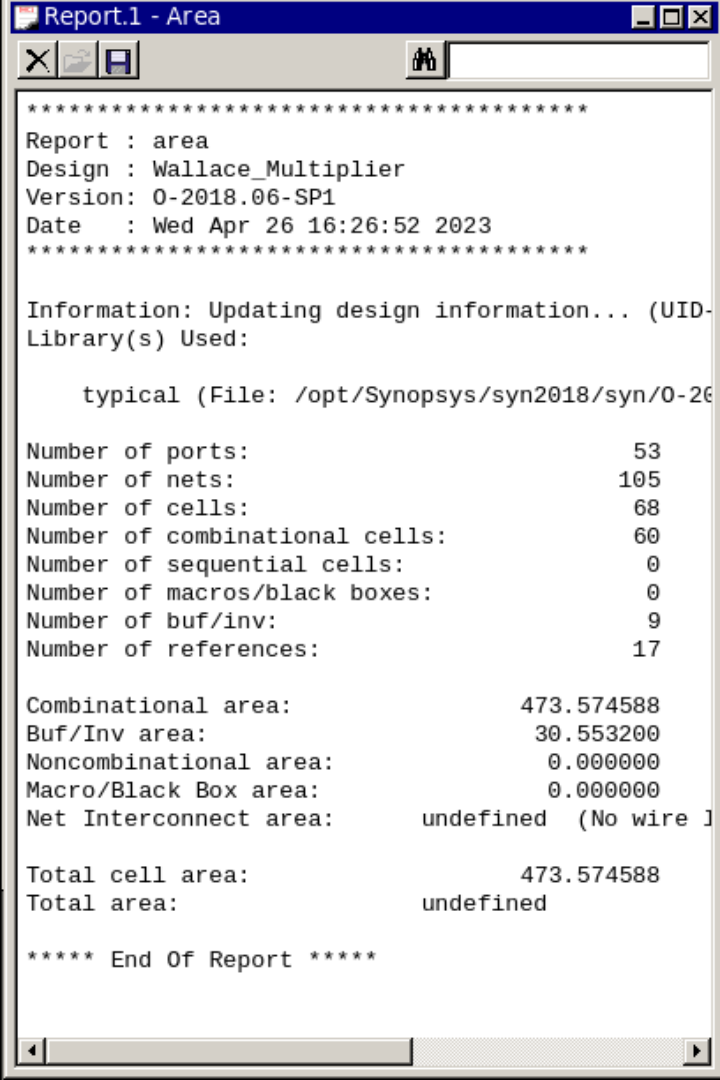
 图5 华莱士树乘法器面积报告

        进位保留乘法器的Verilog代码如下所示。

module Wallace_Multiplier (
    input      [3:0]    A      ,
    input      [3:0]    B      ,
    output  [7:0]    Sum
);

    wire [3:0] partial_product [3:0];  

    wire [3:0] W_level1_c,W_level1_carry;
    wire [3:0] W_level2_c,W_level2_carry;


    assign partial_product[0]=B[0]?A:0;
    assign partial_product[1]=B[1]?A:0;
    assign partial_product[2]=B[2]?A:0;
    assign partial_product[3]=B[3]?A:0;

    // level1
    Adder_half adder_half_u1 (
        .Mult1    (partial_product[0][1]),
        .Mult2    (partial_product[1][0]),
        .Res    (Sum[1]),
        .Carry(W_level1_carry[0])
    ); 

    Adder adder_u1 (
        .Mult1     (partial_product[0][2]),
        .Mult2     (partial_product[1][1]),
        .I_carry (partial_product[2][0]),
        .Res     (W_level1_c[1]),
        .Carry (W_level1_carry[1])
    );

    Adder adder_u2 (
        .Mult1     (partial_product[0][3]),
        .Mult2     (partial_product[1][2]),
        .I_carry (partial_product[2][1]),
        .Res     (W_level1_c[2]),
        .Carry (W_level1_carry[2])
    );

    Adder_half adder_half_u2 (
        .Mult1    (partial_product[1][3]),
        .Mult2    (partial_product[2][2]),
        .Res    (W_level1_c[3]),
        .Carry(W_level1_carry[3])
    ); 

    // level2
    Adder_half adder_half_u3 (
        .Mult1    (W_level1_c[1]),
        .Mult2    (W_level1_carry[0]),
        .Res    (Sum[2]),
        .Carry(W_level2_carry[0])
    ); 

    Adder adder_u3 (
        .Mult1     (W_level1_c[2]),
        .Mult2     (W_level1_carry[1]),
        .I_carry (partial_product[3][0]),
        .Res     (W_level2_c[1]),
        .Carry (W_level2_carry[1])
    );

    Adder adder_u4 (
        .Mult1     (W_level1_c[3]),
        .Mult2     (W_level1_carry[2]),
        .I_carry (partial_product[3][1]),
        .Res     (W_level2_c[2]),
        .Carry (W_level2_carry[2])
    );

    Adder adder_u5 (
        .Mult1     (W_level1_carry[3]),
        .Mult2     (partial_product[2][3]),
        .I_carry (partial_product[3][2]),
        .Res     (W_level2_c[3]),
        .Carry (W_level2_carry[3])
    );
    assign Sum[7:3]={partial_product[3][3],W_level2_c[3:1]}+{W_level2_carry[3:0]};
    assign Sum[0]=partial_product[0][0];
endmodule