📙作者简介： 清水加冰，目前大二在读，正在学习C/C++、Python、操作系统、数据库等。

📘相关专栏：C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。

欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正！

✨每一次努力都是一种收获，每一次坚持都是一种成长✨       

目录

 前言

构建二叉树

 销毁二叉树

 二叉树的递归遍历

 二叉树节点个数

 二叉树叶子节点个数

 二叉树第k层节点个数

查找

 二叉树的高度

二叉树的层序遍历

判断是否是完全二叉树

 总结

---

 前言

        前边的内容陆续的对二叉树的内容进行了介绍，但也并没有系统的将二叉树各部分的操作进行实现，本期将会对二叉树的一些基本操作进行实现。

---

构建二叉树

        二叉树的基本操作中不包含插入和删除操作（没有意义），在后续更为复杂的树形结构中才有使用价值，这里就不再进行实现。

        之前都是一直手动构建二叉树，一个一个的创建节点连接，在创建二叉树时我们还可以通过递归创建二叉树。牛客上边也有相关题目：

二叉树的构建及遍历

         我们也以这道题目为例，来进行构建二叉树。题目给的要求是根据输入的字符串来构建二叉树，#就代表为NULL。最后我们返回这棵树的根即可。

 在此之前我们先定义一下二叉树：

typedef char Datatype;
typedef struct BinaryTree
{
	Datatype data;
	struct BinaryTree* left;
	struct BinaryTree* right;
}BTNode;

        根据输入的字符串来进行二叉树的构建。传进来一个一个数组，链式二叉树的构建最简洁的是使用递归，但是我们也需要有一个变量控制一下遍历的字符位置，在函数里创建一个变量不好进行传参，所以我们最好在调用函数里创建一个变量，然后取地址传参。

具体代码如下：

BTNode* CreatBTNode(char* str,int* pi)
{
    if(str[*pi]=='#')
    {
        (*pi)++;
        return NULL;
    }
    //创建节点
    BTNode* root =(BTNode*)malloc(sizeof(BTNode));
    //节点赋值
    root->data=str[*pi];
    (*pi)++;
    //连接
    root->left=CreatBTNode(str,pi);
    root->right=CreatBTNode(str,pi);

    return root;
}

 销毁二叉树

        销毁二叉树需要注意二叉树根的置空，这里我们可以使用一级指针也可以使用二级指针。

 使用一级指针置空root时需要调用销毁函数后手动置空。销毁二叉树同样也需要利用递归遍历二叉树，然后逐一销毁。

 二级指针：

void TreeDestroy(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}

	TreeDestroy(&(*root)->left);
	TreeDestroy(&(*root)->right);
	free(*root);
	root = NULL;
}

一级指针：

void TreeDestroy(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
	
}

 二叉树的递归遍历

 遍历的内容较为简单，前边文章也介绍过，这里作为整合，详细可见：数据结构入门指南：二叉树

代码如下：

//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}
//后续遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);

}

 二叉树节点个数

这个就很简单了，我们前边也实现过，就不再详细介绍。详细可见文章：二叉树】——链式结构（快速掌握递归与刷题技巧）

int TreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

 二叉树叶子节点个数

这部分是对节点个数的一个进阶，代码如下：

int BinaryTreeLeafSize(BTNode* root)
{
	if (root==NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

 二叉树第k层节点个数

之前文章中讲过，这里就整合一下，不进行详细介绍，代码如下：

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

查找

         二叉树查找部分不难，但存在坑，我们依然是使用递归遍历来查找，如果root为NULL就返回NULL，找到符合的data就返回当前节点。在查找时其实就是对二叉树的一种遍历，我们先判断当前节点是否符合，再判断左子树和右子树。它其实考察的就是二叉树的前序遍历。

BTNode* TreeFind(BTNode* root, char x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	else
	{
		BTNode* ret1=TreeFind(root->left, x);
		BTNode* ret2=TreeFind(root->right, x);
		return ret1 != NULL ? ret1 : ret2;
	}
}

         最后返回时返回不为NULL的那个，所以我们这里是先假设：ret1！=NULL，不为NULL就返回ret1，否则（ret1为NULL），就返回ret2。

         或许有人会有疑问为什么不直接使用运算符还要创建两个变量来接收返回值？

        这里我们要明白，如果直接将递归带入运算符，那么它在判断条件时就会执行一次，在最终结果时又会执行一遍，这样虽然不会造成空间上多大的浪费，但在时间上就会大大降低，每使用一次就会递归一次，这都是时间的消耗。

 二叉树的高度

        要计算二叉树的高度，也就是找出左子树和右子树中层数最高的然后加一。当遇到节点为NULL就返回0。

 代码如下：

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

二叉树的层序遍历

         二叉树的层序遍历与之前的递归遍历二叉树又有所不同，层序遍历需要使用到队列的数据结构。层序遍历是属于广度优先的遍历，而前序遍历属于深度优先的遍历

 前边的递归遍历是通过根（root）找到左子树，右子树，然后一直不断的向下遍历。而层序遍历不同，它是通过一层带一层的方法来遍历的，过程如下图：

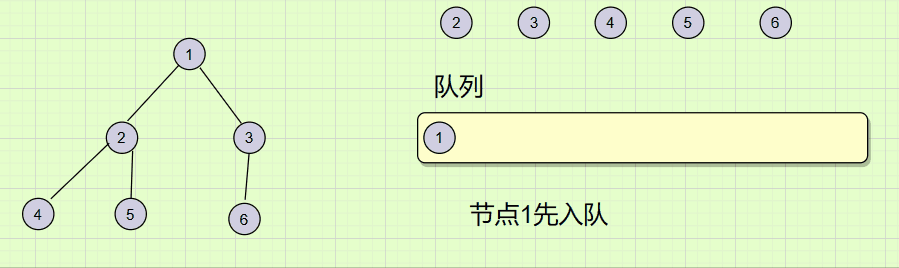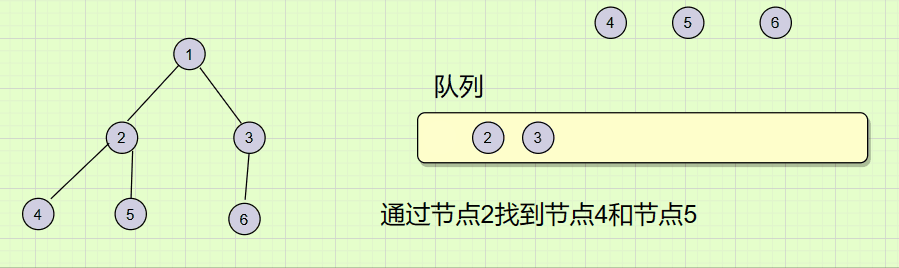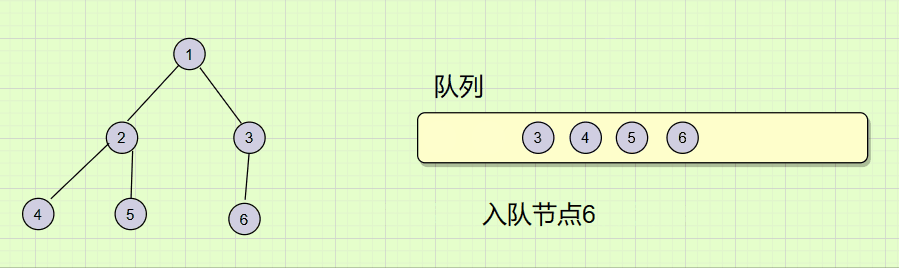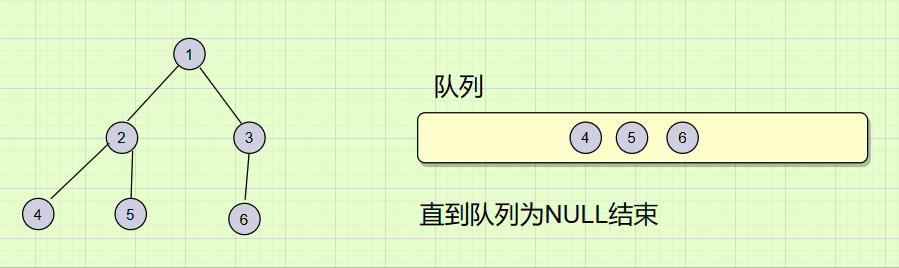
 要实现层序遍历首先我们需要有一个队列的数据结构（可以拷贝之前的C语言代码），然后通过不断的入队出队操作，来实现一层带一层的遍历。

void LayerTraver(BTNode* root)
{
	Que q;//创建队列
	QueueInit(&q);//初始化队列
	if(root)//判断根是否为NULL，不为NULL就入队
		QueuePush(&q, root);
	while (!IsEmpty(&q))
	{
		BTNode* front= QueueFront(&q);//取队头数据

        //通过队头数据找到左右子节点

		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
        //输出队头节点的数据，也可以存放到数组中
		printf("%d ", front->data);
        //队头节点的左右子节点入队之后，将节点1出队
		QueuePop(&q);
	}
	DestoryQueue(&q);
}

判断是否是完全二叉树

         通过层序遍历的原理，我们还可以通过层序遍历来解决判断完全二叉树的问题。在入队时如果第一次遇到NULL就跳出循环，然后再入队，如果入队的有非空节点，就返回false，没有则返回true。代码如下：

int TreeComplete(BTNode* root)
{
	Que q;
	QueueInit(&q);

	if (root)
		QueuePush(&q, root);

	while (!IsEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		if (front == NULL)//第一次遇到NULL，跳出循环
			break;

		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
		QueuePop(&q);
	}
//再次进行层序遍历，入队
	while (!IsEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
        //如果取到的队头节点有非空节点，则不是完全二叉树
		if (front != NULL)
		{
			DestoryQueue(&q);
			return false;
		}
	}
//没有非空节点最后返回true
	DestoryQueue(&q);
	return true;
}

---

 总结

        以上便是本期全部内容，二叉树篇到此结束，本篇文章是对二叉树一些基本操作的整合，以及层序遍历的介绍与讲解，希望可以帮到你，最后，感谢阅读！