实验二B 图像的空域与频域滤波（源代码一站式复制粘贴）

news2024/11/21 2:23:48

实验二B 图像的空域与频域滤波

  • 一、实验目的
  • 二、实验原理
  • 三、实验内容与要求
  • 四、实验的具体实现

一、实验目的

1.掌握图像滤波的基本定义及目的。
2.理解空间域滤波的基本原理及方法。
3.掌握进行图像的空域滤波的方法。
4.掌握傅里叶变换及逆变换的基本原理方法。
5.理解频域滤波的基本原理及方法。
6.掌握进行图像的频域滤波的方法。

二、实验原理

1.频域增强
频域增强是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其他空间中，然后利用该空间的特有性质方便地进行图像处理，最后再转换回原来的图像空间中，从而得到处理后的图像。
频域增强的主要步骤是：
1）选择变换方法，将输入图像变换到频域空间。
2）在频域空间中，根据处理目的设计一个传递函数，并进行处理。
3）将所得结果用逆变换得到增强的图像。
4）常用的频域增强方法有低通滤波和高通滤波。
2.低通滤波
图像的能量大部分集中在幅度谱的低频和中频部分，而图像的边缘和噪声对应于高频部分。因此能降低高频成分幅度的滤波器就能减弱噪声的影响。由卷积定理，在频域实现低通滤波的数学表达式：
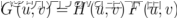
在这里插入图片描述

1)理想低通滤波器（ILPF）

2)巴特沃斯低通滤波器（BLPF）

3)指数型低通滤波器（ELPF）

3.高通滤波
由于图像中的细节部分与其高频分量相对应，所以高通滤波可以对图像进行锐化处理。高通滤波与低通滤波相反，它是高频分量顺利通过，使低频分量受到削弱。高通滤波器和低通滤波器相似，其转移函数分别为:
1)理想高通滤波器（IHPF）

2)巴特沃斯高通滤波器（BLPF）

3)指数型高通滤波器（ELPF）

图像经过高通滤波处理后，会丢失许多低频信息，所以图像的平滑区基本上会消失。所以，可以采用高频加强滤波来弥补。高频加强滤波就是在设计滤波传递函数时，加上一个大于0小于1的常数，即：

三、实验内容与要求

1.傅里叶变换
1)读出一幅灰度图像，对其进行快速傅里叶变换，分别显示其幅度图像和相位图像。
2)仅对相位部分进行傅里叶逆变换后查看结果图像。
3)仅对幅度部分进行傅里叶逆变换后查看结果图像。
4)将图像的傅里叶变换置为其共轭后进行逆变换，比较新生成图像与原始图像的差异。
2.平滑频域滤波
1)设计理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器，截止频率自选。
2)读出一幅灰度图像，分别采用理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器对其进行滤波（截止频率自选），再做逆变换，观察不同的截止频率下采用不同低通滤波器得到的图像与原图像的区别，特别注意振铃效应。
3.锐化频域滤波
1)设计理想高通滤波器、巴特沃斯高通滤波器和高斯高通滤波器，截止频率自选。
2)读出一幅灰度图像，分别采用理想高通滤波器、巴特沃斯高通滤波器和高斯高通滤波器对其进行滤波（截止频率自选），再做逆变换，观察不同的截止频率下采用不同高通滤波器得到的图像与原图像的区别。

四、实验的具体实现

%% 傅里叶变换
% 1)读出一幅灰度图像，对其进行快速傅里叶变换，分别显示其幅度图像和相位图像。
img=imread('Fig0219(a).tif');
f1=fft2(img);%快速傅里叶变换
f2=log(1+abs(f1));%振幅谱
f3=fftshift(f1);
f4=angle(f1);%相位谱
figure(1)
subplot(1,3,1),imshow(img),title('Original Image');
subplot(1,3,2),imshow(f2,[]),title('amplitude Image');
subplot(1,3,3),imshow(f4),title('pahse Image');
% 2)仅对相位部分进行傅里叶逆变换后查看结果图像。
f=ifft2(abs(f1));
figure(2)
subplot(2,3,1),imshow(img),title('Original Image');
subplot(2,3,2),imshow(f4),title('pahse Image');
subplot(2,3,3),imshow(log(1+abs(f)),[]),title('abspahse Image');
% 3)仅对幅度部分进行傅里叶逆变换后查看结果图像。
f=ifft2(abs(f1));
subplot(2,3,4),imshow(img),title('Original Image');
subplot(2,3,5),imshow(f2,[]),title('amplitude Image');
subplot(2,3,6),imshow(log(1+abs(f)),[]),title('absamplitude Image');
% 4)将图像的傅里叶变换 置为其共轭后进行逆变换，比较新生成图像与原始图像的差异。
%img=imread('Fig0427(a).tif');
f1=fft2(img);
f2=log(1+abs(f1));
f3=fftshift(f1);
f4=angle(f1);
f5=-f4;
f6=double(f3.*exp(f4));%傅里叶变换的复共轭
f7=ifft2(f6);%反傅里叶变换
figure(3)
subplot(1,2,1),imshow(img),title('Original Image');
subplot(1,2,2),imshow(real(f7),[]),title('inverse fourier transform');

%% 2.平滑频域滤波
%1)设计理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器，截止频率自选。
%%%%%理想低通滤波器透视图%%%%%
a=100;
b=100;
U=0:a;
V=0:b;
M=length(U);N=length(V);
D0=10;%频带中心半径
x1=50;y1=50;
x0=-50;y0=-50;
m=fix(M/2);n=fix(N/2);
H=zeros(M,N);
n=2;
for u=1:M
    for v=1;N
        a=sqrt((U(u)-50).*(U(u)-50)+(V(v)-50).*(V(v)-50));%D(u,v)
        if (a<=D0)%理想滤波器
            H(u,v)=1;
        else
            H(u,v)=0;
        end
    end
end
%figure(4);subplot(1,3,1),surf(U,V,H),title('理想低通滤波透视图');
%%%%%2阶巴特沃斯低通滤波透视图%%%%%
a=100;
b=100;
U=0:a;
V=0:b;
M=length(U);
N=length(V);
D0=10;%频带中心半径
x1=50;y1=50;
x0=-50;y0=-50;
m=fix(M/2);n=fix(N/2);
H=zeros(M,N);
n=2;
for u=1:M
    for v=1;N
        a=sqrt((U(u)-50).*(U(u)-50)+(V(v)-50).*(V(v)-50));%D(u,v)
        b=1+(a/D0)^2*n;
        H(u,v)=1/b;
    end
end
%subplot(1,3,2),surf(U,V,H),title('2阶巴特沃斯低通滤波透视图');
%%%%%高斯低通滤波透视图%%%%%
a=100;
b=100;
U=0:a;
V=0:b;
M=length(U);
N=length(V);
D0=10;%频带中心半径
x1=50;y1=50;
x0=-50;y0=-50;
m=fix(M/2);n=fix(N/2);
H=zeros(M,N);
n=2;
for u=1:M
    for v=1;N
        D1=((u-m-x0)^2+(v-n-y0).^2)^0.5;
        D2=((u-m+x0)^2+(v-n+y0).^2)^0.5;
        D11=((u-m-x1)^2+(v-n-y1).^2)^0.5;
        D21=((u-m+x1)^2+(v-n+y1).^2)^0.5;
        H(u,v)=((U(u)-50).*(U(u)-50)+(V(v)-50).*(V(v)-50));%D(u,v)
    end
end
%subplot(1,3,3),surf(U,V,H),title('高斯低通滤波透视图');
%2)读出一幅灰度图像，分别采用理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器对其进行滤波（截止频率自选），再做逆变换，观察不同的截止频率下采用不同低通滤波器得到的图像与原图像的区别，特别注意振铃效应。
%%
%%%%%d0=15理想低通滤波%%%%%
f=double(img);
g=fft2(f);%傅里叶变换
g=fftshift(g);
[M,N]=size(g);
d0=15;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        if(d<=d0)
            h=1;
        else 
            h=0;
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
figure(5),
subplot(2,2,1),imshow(img),title('Original Image');
subplot(2,2,2),imshow(J2),title('d0=15 lowpass filter');
%%%%%d0=50理想低通滤波%%%%%
d0=50;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        if(d<=d0)
            h=1;
        else 
            h=0;
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,3),imshow(J2),title('d0=50 lowpass filter');
%%%%%d0=100理想低通滤波%%%%%
d0=100;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        if(d<=d0)
            h=1;
        else 
            h=0;
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,4),imshow(J2),title('d0=100 lowpass filter');

%%
%%%%%d0=15 2阶巴特沃斯低通滤波%%%%%
nn=2;
d0=15;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=1/(1+0.414*(d/d0)^(2*nn));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
figure(6),
subplot(2,2,1),imshow(img),title('Original Image');
subplot(2,2,2),imshow(J2),title('d0=15 Butterworth lowpss filter');
%%%%%d0=50 2阶巴特沃斯低通滤波%%%%%
d0=50;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=1/(1+0.414*(d/d0)^(2*nn));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,3),imshow(J2),title('d0=50 Butterworth lowpss filter');
%%%%%d0=100 2阶巴特沃斯低通滤波%%%%%0;
d0=100;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=1/(1+0.414*(d/d0)^(2*nn));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,4),imshow(J2),title('d0=100 lButterworth lowpss filter');

%%
%%%%%d0=15 高斯低通滤波%%%%%
d0=15;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=exp(-(d.^2)./(2*(d0^2)));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
figure(7),
subplot(2,2,1),imshow(img),title('Original Image');
subplot(2,2,2),imshow(J2),title('d0=15 Gaussian filter');
%%%%%%d0=50 高斯低通滤波%%%%%
d0=30;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=exp(-(d.^2)./(2*(d0^2)));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,3),imshow(J2),title('d0=50 Guassian filter');
%%%%%%d0=100 高斯低通滤波%%%%%
d0=100;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=exp(-(d.^2)./(2*(d0^2)));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,4),imshow(J2),title('d0=100 Guassian filter');

%% 3.锐化频域滤波
%1)设计理想高通滤波器、巴特沃斯高通滤波器和高斯高通滤波器，截止频率自选。
%%%%%理想高通滤波器透视图%%%%%
a=100;
b=100;
U=0:a;
V=0:b;
M=length(U);N=length(V);
D0=15;%频带中心半径
H=zeros(M,N);
n=2;
for u=1:M
    for v=1;N
        a=sqrt((U(u)-50).*(U(u)-50)+(V(v)-50).*(V(v)-50));%D(u,v)
        if (a>=D0)%理想滤波器
            H(u,v)=1;
        else
            H(u,v)=0;
        end
    end
end
figure(8);
subplot(1,3,1),surf(U,V,H),title('理想高通滤波透视图');
%%%%%2阶巴特沃斯高通滤波透视图%%%%%
a=100;
b=100;
U=0:a;
V=0:b;
M=length(U);
N=length(V);
D0=15;%频带中心半径
x1=50;y1=50;
x0=-50;y0=-50;
m=fix(M/2);n=fix(N/2);
H=zeros(M,N);
n=2;
for u=1:M
    for v=1;N
        a=sqrt((U(u)-50).*(U(u)-50)+(V(v)-50).*(V(v)-50));%D(u,v)
        b=1+(a/D0)^2*n;
        H(u,v)=-1/b;
    end
end
subplot(1,3,2),surf(U,V,H),title('2阶巴特沃斯高通滤波透视图');
%%%%%高斯高通滤波透视图%%%%%
a=100;
b=100;
U=0:a;
V=0:b;
M=length(U);
N=length(V);
D0=15;%频带中心半径
x1=50;y1=50;
x0=-50;y0=-50;
m=fix(M/2);n=fix(N/2);
H=zeros(M,N);
for u=1:M
    for v=1;N
        D1=((u-m-x0)^2+(v-n-y0).^2)^0.5;
        D2=((u-m+x0)^2+(v-n+y0).^2)^0.5;
        D11=((u-m-x1)^2+(v-n-y1).^2)^0.5;
        D21=((u-m+x1)^2+(v-n+y1).^2)^0.5;
        H(u,v)=((U(u)-50).*(U(u)-50)+(V(v)-50).*(V(v)-50));%D(u,v)
    end
end
subplot(1,3,3),surf(U,V,H),title('高斯高通滤波透视图');
%2)读出一幅灰度图像，分别采用理想高通滤波器、巴特沃斯高通滤波器和高斯高通滤波器对其进行滤波（截止频率自选），再做逆变换，观察不同的截止频率下采用不同高通滤波器得到的图像与原图像的区别。
%%
%%%%%d0=15理想高通滤波%%%%%
f=double(img);
g=fft2(f);%傅里叶变换
g=fftshift(g);
[M,N]=size(g);
d0=15;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        if(d>=d0)
            h=1;
        else 
            h=0;
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
figure(9),
subplot(2,2,1),imshow(img),title('Original Image');
subplot(2,2,2),imshow(J2),title('d0=15 high filter');
%%%%%d0=30理想低通滤波%%%%%
d0=30;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        if(d>=d0)
            h=1;
        else 
            h=0;
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,3),imshow(J2),title('d0=30 high filter');
%%%%%d0=60理想高通滤波%%%%%
d0=60;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        if(d>=d0)
            h=1;
        else 
            h=0;
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,4),imshow(J2),title('d0=60 high filter');

%%
%%%%%d0=15 2阶巴特沃斯低通滤波%%%%%
nn=2;
d0=15;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        if(d==0)
            h=0;
        else
            h=1/(1+0.414*(d0/d)^(2*nn));
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
figure(10),
subplot(2,2,1),imshow(img),title('Original Image');
subplot(2,2,2),imshow(J2),title('d0=15 Butterworth high filter');
%%%%%d0=30 2阶巴特沃斯低通滤波%%%%%
d0=30;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
         d=sqrt((i-m)^2+(j-n)^2);
        if(d==0)
            h=0;
        else
            h=1/(1+0.414*(d0/d)^(2*nn));
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,3),imshow(J2),title('d0=30 Butterworth high filter');
%%%%%d0=60 2阶巴特沃斯高通滤波%%%%%0;
d0=60;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
         d=sqrt((i-m)^2+(j-n)^2);
        if(d==0)
            h=0;
        else
            h=1/(1+0.414*(d0/d)^(2*nn));
        end
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,4),imshow(J2),title('d0=60 lButterworth high filter');

%%
%%%%%d0=15 高斯高通滤波%%%%%
d0=15;
n=2;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=1-exp(-(d.^2)./(2*(d0^2)));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
figure(11),
subplot(2,2,1),imshow(img),title('Original Image');
subplot(2,2,2),imshow(J2),title('d0=15 Gaussian filter');
%%%%%%d0=30 高斯高通滤波%%%%%
d0=30;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=1-exp(-(d.^2)./(2*(d0^2)));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,3),imshow(J2),title('d0=30 Guassian filter');
%%%%%%d0=60 高斯低通滤波%%%%%
d0=60;
m=fix(M/2);n=fix(N/2);
for i=1:M
    for j=1:N
        d=sqrt((i-m)^2+(j-n)^2);
        h=1-exp(-(d.^2)./(2*(d0^2)));
        result(i,j)=h*g(i,j);
    end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(2,2,4),imshow(J2),title('d0=60 Guassian filter');

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/106254.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

算法刷题打卡第52天：排序数组---桶排序

算法刷题打卡第52天：排序数组---桶排序

排序数组 难度&#xff1a;中等 给你一个整数数组 nums&#xff0c;请你将该数组升序排列。 示例 1&#xff1a; 输入&#xff1a;nums [5,2,3,1] 输出&#xff1a;[1,2,3,5]示例 2&#xff1a; 输入&#xff1a;nums [5,1,1,2,0,0] 输出&#xff1a;[0,0,1,1,2,5]桶排序…
阅读更多...
2022 CSDN 客服年终总结

2022 CSDN 客服年终总结

hello&#xff0c;大家好&#xff0c;这里是《听用户心声&#xff0c;解用户之需》之 2022 年终总结篇。 秉承“用户至上”的服务理念&#xff0c;为了给用户提供极致的服务体验而时刻努力着&#xff0c;2022年&#xff0c;在大家的一致努力下&#xff0c;究竟有何成效呢&#…
阅读更多...
SpringBoot1:helloword、导入依赖、配置项设置，打包方法、lombok、dev-tools、Spring Initailizr、常见注解

SpringBoot1:helloword、导入依赖、配置项设置，打包方法、lombok、dev-tools、Spring Initailizr、常见注解

1.简介 简化Spring开发的一个框架。对整个Spring技术栈的大整合 J2EE企业级开发的一站式解决方案。 2.微服务 一个应用应该是一组小型服务&#xff0c;可以通过HTTP的方式来进行互通 每一个功能元素都是可独立替换&#xff0c;和独立升级的软件单元。 3.HelloWord 功能&am…
阅读更多...
Stm32标准库函数5——OV2640 PA0-7 F103C8T6 4500000 联合VB 高分辨率

Stm32标准库函数5——OV2640 PA0-7 F103C8T6 4500000 联合VB 高分辨率

stm32f103c8t6串口发送 OV2640的图像&#xff0c;分辨率可选。网络上资料大部分是低分辨率的&#xff0c;这个可以做高分辨率 完整工程打包&#xff0c;包含VB串口显示界面&#xff1a; https://download.csdn.net/download/fengyuzhe13/87327054https://download.csdn.net/do…
阅读更多...
【经典问题：HanoiTower（汉诺塔）】

【经典问题：HanoiTower（汉诺塔）】

&#x1f381;HanoiTower&#x1f385;HanoiTower问题描述&#x1f385;&#x1f385;模拟推导&#x1f385;&#x1f385;&#x1f385;问题的两种形式&#x1f384;求解移动总次数&#x1f384;&#x1f384;打印详细的移动过程&#x1f385;HanoiTower问题描述 汉诺塔问题&a…
阅读更多...
基于HMM模型实现中文分词

基于HMM模型实现中文分词

任务描述：在理解中文文本的语义时需要进行分词处理，分词算法包括字符串匹配算法，基于统计的机器学习算法两大类。本案例在前文将说明常用分词库及其简单应用，之后会通过中文分词的例子介绍和实现一个基于统计的中文分词方法——HMM模型，该模型能很好地处理歧义和未登录词问…
阅读更多...
[含文档+源码等]基于SSM实现的宿舍公共财产管理系统|寝室

[含文档+源码等]基于SSM实现的宿舍公共财产管理系统|寝室

博主介绍&#xff1a;✌在职Java研发工程师、专注于程序设计、源码分享、技术交流、专注于Java技术领域和毕业设计✌ 项目名称 [含文档源码等]基于SSM实现的宿舍公共财产管理系统|寝室 演示视频 [含文档源码等]基于SSM实现的宿舍公共财产管理系统|寝室_哔哩哔哩_bilibili 系统介…
阅读更多...
经济低迷形势下，如何降低软件开发成本？

经济低迷形势下，如何降低软件开发成本？

1、选对开发方法 过程决定结果。方法错了&#xff0c;再有经验的人&#xff0c;结果也不会好。例如&#xff0c;软件开发方法从70年代的瀑布&#xff0c;一步步从迭代、快速原型等进化到现在的敏捷、规模化敏捷、DevOps等。统计数字显示&#xff0c;使用敏捷方法&#xff0c;平…
阅读更多...
Excel中实现时间相减，得到间隔时间（年月日时分秒）

Excel中实现时间相减，得到间隔时间（年月日时分秒）

一、年月日之差 表中有开始日期和结束日期&#xff0c;我们在D3单元格中输入“C3-B3” 于是&#xff0c;得到下面的结果 很显然&#xff0c;结果并不是我们想要的。说明这种方法不行&#xff0c;为了得到两个日期之间的时间间隔&#xff0c;需要用到DATEDIF函数。先来说下DATED…
阅读更多...
我国融资性担保行业整体呈减量提质趋势 国家“出手”解决行业痛点

我国融资性担保行业整体呈减量提质趋势 国家“出手”解决行业痛点

根据观研报告网发布的《中国融资性担保行业发展趋势分析与投资前景预测报告&#xff08;2022-2029年&#xff09;》显示&#xff0c;融资性担保行业是指担保人与银行业金融机构等债权人约定&#xff0c;当被担保人不履行对债权人负有的融资性债务时&#xff0c;由担保人依法承担…
阅读更多...
Go：使用 go-micro 构建微服务（一）

Go：使用 go-micro 构建微服务（一）

一、微服务 什么是微服务&#xff08;microservice&#xff09;&#xff1f;这是企业界正在向计算界提出的问题。一个产品的可持续性取决于它的可修改程度。 大型产品如果不能正常维护&#xff0c;就需要在某个时间点停机维护。而微服务架构用细化的服务取代了传统的单体服务…
阅读更多...
语音识别芯片LD3320介绍再续

语音识别芯片LD3320介绍再续

语音识别芯片LD3320驱动程序 1、芯片复位 复位就是对LD3320芯片的第47腿&#xff08;RSTB*&#xff09;发送低电平&#xff0c;然后需要对片选CS做一次拉低→拉 高的操作&#xff0c;以激活内部DSP。按照以下顺序&#xff1a; void LD_reset() { RSTB1;delay(1);RSTB0;delay…
阅读更多...
TencentOS 3.1下安装zabbix 5.0.30

TencentOS 3.1下安装zabbix 5.0.30

TencentOS是使用官方镜像文件安装的虚拟机。 虚拟机为virtualBox 6.1 zabbix 使用zabbix官方安装包编译安装。 下载地址： Download Zabbix sources zabbix软件包解包，本次安装解包在/opt下 zabbix需要nginx、php、mysql等软件支持，因此先安装它们。 安装mysql如下： yu…
阅读更多...
Usaco Training刷怪旅 第二层第二题：Transformations

Usaco Training刷怪旅 第二层第二题：Transformations

usaco training 关注我持续更新usaco training A square pattern of size N x N (1 < N < 10) black and white square tiles is transformed into another square pattern. Write a program that will recognize the minimum transformation that has been applied to t…
阅读更多...
QCon直击｜闲鱼推荐大规模应用背后的工程实践

QCon直击｜闲鱼推荐大规模应用背后的工程实践

讲师介绍闲鱼技术部 | 吴白万小勇&#xff08;吴白&#xff09;&#xff0c;闲鱼服务端专家。毕业于南京大学计算机系&#xff0c;目前负责闲鱼技术推荐架构。推荐在闲鱼的应用不同于搜索的确定性&#xff0c;推荐场景面临的问题往往是不确定的。但是正是因为这种不确定&#x…
阅读更多...
Kafka无法对外暴露端口的相关解决方案

Kafka无法对外暴露端口的相关解决方案

1、kafka开放外部访问 1.1、修改kafka configMap 修改内容如下 # 修改EXTERNAL_ACCESS_IP变量&#xff0c;值为真实的外网IP export EXTERNAL_ACCESS_IP${真实的外网IP} 1.2、重启kafka # 重启kafka kubectl rollout restart statefulset kafka -n default # 查看kafka状态 k…
阅读更多...
盛邦安全将于12月27日上会，2022年前三季度收入1亿元

盛邦安全将于12月27日上会，2022年前三季度收入1亿元

12月20日&#xff0c;上海证券交易所披露的科创板上市委2022年第112次审议会议公告显示&#xff0c;远江盛邦&#xff08;北京&#xff09;网络安全科技股份有限公司&#xff08;下称“盛邦安全”&#xff09;将于2022年12月27日上会。 目前&#xff0c;盛邦安全已经提交了招股…
阅读更多...
在tushare量化平台可以获取哪些数据？

在tushare量化平台可以获取哪些数据？

沪深股票数据是Tushare量化最传统、最具历史意义的数据服务项目从一开始就为投资者特别是定量投资者提供了稳定、方便的接口。 1.基础数据 提供交易和回测所需要的基础信息&#xff0c;目前主要提供的是上市公司股票列表和交易日历等 2.行情数据 行情数据目前还在继续规则和…
阅读更多...
“史上最贵”卡塔尔世界杯，有哪些炫酷的“黑科技”？

“史上最贵”卡塔尔世界杯，有哪些炫酷的“黑科技”？

2022年卡塔尔世界杯投入超过2200亿美元&#xff0c;堪称“史上最贵世界杯”。这些投入不仅用在了场馆、道路等基础设施建设中&#xff0c;也体现在让人震撼的芯片传感器、人工智能、先进技术等“黑科技”上。今年的卡塔尔世界杯有什么“科技感十足”的先进技术&#xff1f;让我…
阅读更多...
坐标系相关整理

坐标系相关整理

参考url:https://www.jianshu.com/p/06890af3d780 Dicom坐标系 x轴&#xff1a;从右手到左手 y轴&#xff1a;从前胸到后背 z轴&#xff1a;从脚到头 解刨学坐标系 医学人体三解剖面&#xff0c;医疗影像三维图&#xff0c;主要是针对人体来说。解剖学上的坐标体系&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023