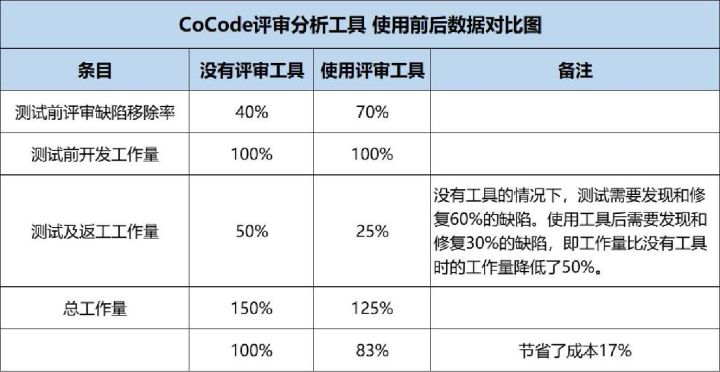
排序数组

难度：中等

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

桶排序

思路：
假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序)。

为了使桶排序更加高效，我们需要做到这两点:

1. 在额外空间充足的情况下，尽量增大桶的数量
2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

什么时候最快： 当输入的数据可以均匀的分配到每一个桶中。
什么时候最慢： 当输入的数据被分配到了同一个桶中

样例如下：

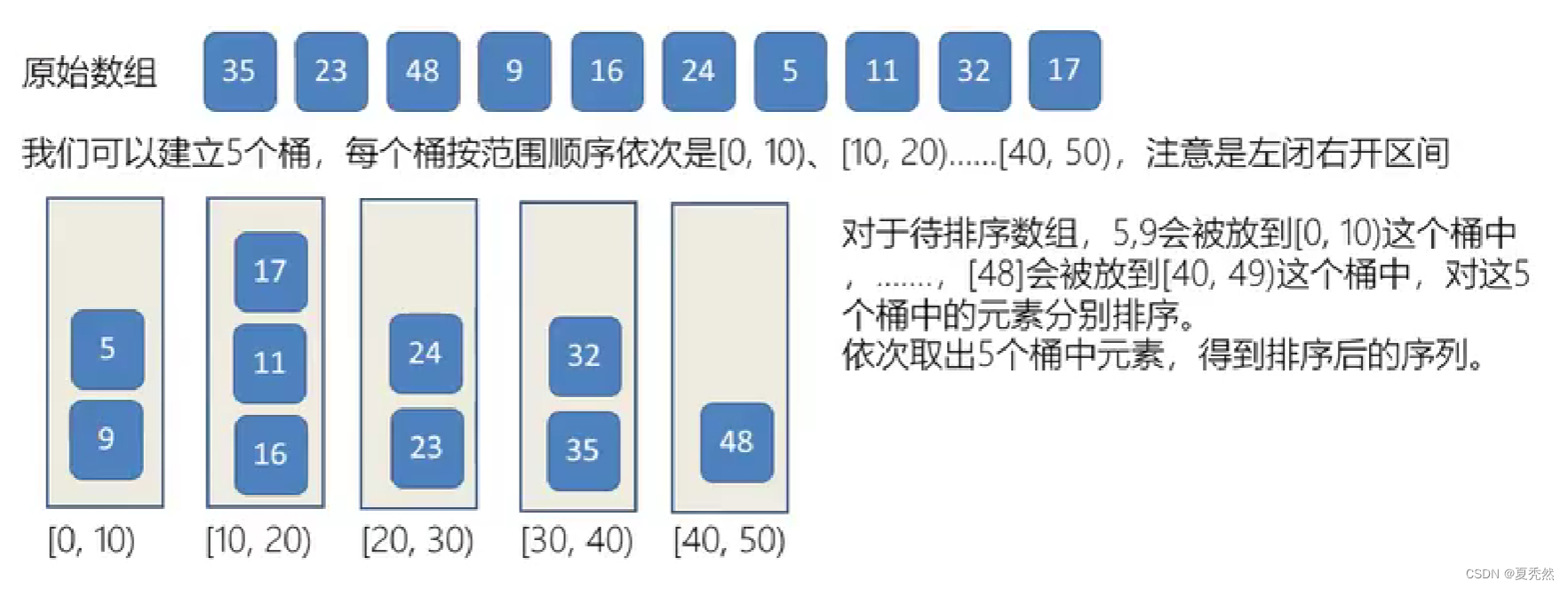
在桶排序中保证元素均匀分布到各个桶尤为关键。举个反例，有数组 [0,9,4,5,8,7,6,3,2,1] 要排序，它们都是10以下的数，如果还按照上面的范围[0,10)建立桶，全部的元素将进入同一个桶中，此时桶排序就失去了意义。实际情况我们很可能事先就不知道输入数据是什么，为了保证元素均匀分不到各个桶中，需要建立多少个桶，每个桶的范围是多少呢？其实我们可以这样：简单点，首先限定桶的容量，再根据元素的个数来决定桶的个数。当然使用更复杂的方法也是可以的。

桶排序利用函数的映射关系，减少了几平所有的比较工作。实际上，桶排序的)值的计算，其作用就相当于快排中划分，已经把大量数据分割成了基本有序的数据块(桶)。然后只需要对桶中的少量数据做先进的比较排序即可。

时间复杂度： $O(n+k)$，$n$ 为数字长度，$k$ 为 “桶的个数”，这个仅为分桶的时间复杂度，还需要加上桶内排序的时间复杂度。
空间复杂度： $O(n+k)$，$n$ 为数字长度，$k$ 为 “桶的个数”。

class Solution:
    # 冒泡排序优化版
    def bubbleSort(self, nums):
        length = len(nums)
        for i in range(length - 1):
            # 记录排序状态，如果进行某次冒泡操作没有需要更换位置的情况，则直接退出循环，排序完成
            isSorted = True 
            for j in range(length - 1 - i):
                if nums[j] > nums[j+1]:
                    nums[j], nums[j+1] = nums[j+1], nums[j]
                    isSorted = False
            if isSorted:
                break
        return nums

    # 桶排序
    def bucketSort(self, nums, bucketCup):
        # 初始化桶，每个桶的区间为bucketCup
        min_num, max_num = min(nums), max(nums)
        bucket_size = (max_num - min_num) // bucketCup
        bucket = [[] for i in range(bucket_size+1)]
        # 入桶
        for x in nums:
            bucket[(x - min_num) // bucketCup].append(x)
        # 桶内采用冒泡排序
        for i in range(len(bucket)):
            bucket[i] = self.bubbleSort(bucket[i])
        # 出桶返回排序结果
        return [j for i in bucket for j in i]

    def sortArray(self, nums: List[int]) -> List[int]:
        # 进行桶排序+冒泡排序，设定每个桶的间隔为10
        return self.bucketSort(nums, 10)

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/sort-an-array