文章目录
- 前言
- 思路
- 设计思想
- 非递归前序遍历的思路
- 非递归中序遍历的思路
- 非递归后序遍历的思路
- 层序遍历的思路
- 完整代码
- MyBinaryTree.h
- MyBinaryTree.cpp
- Main.cpp
- 效果展示
前言
- 作者水平有限,全部的代码是学习前人+部分原创
- 不要搬代码,一定要借鉴学习,自己动手!!!
思路
设计思想
- 二叉树的创建:采用先序遍历的顺序,依次写出每个非空节点的数值,如果没有孩子节点就用$符号代替。并采用递归的方式进行实现,依次创建根节点、所有的左子树、右子树
- 二叉树的前、中、后序的递归遍历:本质上的遍历顺序都是一样的,只是打印的时机不同,控制好打印的时机即可。
非递归前序遍历的思路
- 栈s初始化;
- 循环直到p为空且栈s为空
- 当p不空时循环
- 输出p->data;
- 将指针p的值保存到栈中;
- 继续遍历p的左子树
- 当p为空,栈s不空,则
- 将栈顶元素弹出至p;
- 准备遍历p的右子树;

- 当p不空时循环
非递归中序遍历的思路
- 栈s初始化;
- 访问左孩子,左孩子存在继续步骤1;
- 左孩子不存在弹出函数栈帧;
- 访问右孩子,右孩子存在继续步骤1;
- 右孩子不存在弹出函数栈帧,访问该节点;
- 弹出函数栈帧,返回上一级函数栈帧。
非递归后序遍历的思路
- 从当前节点开始遍历:
- 若当前节点存在,就存入栈中,并且置节点flag为1(第一次访问),然后访问其左子树;
- 直到当前节点不存在,需要回退,这里有两种情况:
- 当栈顶节点flag为0时,则表明是从左子树回退,这时需置栈顶节点flag为2(第二次访问),然后通过栈顶节点访问其右子树(取栈顶节点用,但不出栈)
- 当栈顶节点flag为1时,则表明是从右子树回退,这时需出栈,并取出栈节点做访问输出。
- 不断重复12,直到当前节点不存在且栈空。
层序遍历的思路
- 从上到下,从左到右,则利用队列存放各子树结点的指针,初始时把根节点入队,当根结点出队后,令其左、右孩子结点入队(空不入队),而左孩子出队时又令它的左右孩子结点入队,……由此便可产生按层次输出的效果。

完整代码
MyBinaryTree.h
#pragma once
#include<iostream>
using namespace std;
typedef char E;
typedef struct TreeNode {
E element;
struct TreeNode* left, * right;
// 在后序遍历时,需要左右子树都被遍历才行,0表示左子树遍历完成,1表示右子树遍历完成
int flag;//标志遍历的状态。
}*Node;
//栈
typedef Node T;//二叉树节点指针
typedef struct StackNode {
T element;
struct StackNode* next;
} *SNode;
//队列
typedef struct QueueNode {
T element;
struct QueueNode* next;
}*QNode;
typedef struct Queue {
QNode front, rear;
}*LinkedQueue;
Node createBiTree(Node& root);//按照先序顺序创建二叉树
void preOrder(Node root);//递归方式进行先序遍历
void inOrder(Node root);//递归方式进行中序遍历
void postOrder(Node root);//递归方式进行后序遍历
//栈操作
void initStack(SNode head);//初始化栈
int pushStack(SNode head, T element);//入栈
int IsEmpty(SNode head);//判断栈是否为空
T peekStack(SNode head);//获取栈顶元素值
T popStack(SNode head);//出栈
void preOrder2(Node root);//非递归先序遍历
void inOrder0(Node root);//非递归中序遍历 低级版
void inOrder2(Node root);//非递归中序遍历 升级版
void postOrder2(Node root);//非递归后序遍历
//队列操作
int initQueue(LinkedQueue queue);//初始化队列
int offerQueue(LinkedQueue queue, T element);//入队列
int isEmpty(LinkedQueue queue);//队列判空
T pollQueue(LinkedQueue queue);//出队
void levelOrder(Node root);//层序遍历
int getDepthTreeNode(Node root);//求二叉树的深度
MyBinaryTree.cpp
#include"MyBinaryTree.h"
//创建二叉树
//注意采用引用的方式,避免浅拷贝的报错
//Program received signal SIGSEGV, Segmentation fault
Node createBiTree(Node& root) {
char ch;
cin >> ch;
if (ch == '$') {
root = NULL;
}
else {
root = (Node)malloc(sizeof(struct TreeNode));
root->element = ch;
createBiTree(root->left);//构建左子树
createBiTree(root->right);//构建右子树
}
return root;
}
//递归方式进行先序遍历
void preOrder(Node root) {
if (root != NULL) {
cout << root->element << " ";
preOrder(root->left);
preOrder(root->right);
}
}
//递归方式进行中序遍历
void inOrder(Node root) {
if (root == NULL) return;
inOrder(root->left);
cout << root->element << " ";
inOrder(root->right);
}
//递归方式进行后序遍历
void postOrder(Node root) {
if (root == NULL) return;
postOrder(root->left);
postOrder(root->right);
cout << root->element << " ";
}
//初始化栈
void initStack(SNode head) {
head->next = NULL;
}
//入栈
int pushStack(SNode head, T element) {
SNode node = (SNode)malloc(sizeof(struct StackNode));
if (node == NULL) return 0;
node->next = head->next;
node->element = element;//element都是节点
head->next = node;
return true;
}
//判空
int IsEmpty(SNode head) {
return head->next == NULL;
}
//用于获取栈顶元素的值,但是不出栈,仅仅是值获取
T peekStack(SNode head) {
return head->next->element;//返回栈中的首节点的地址
}
//出栈
T popStack(SNode head) {
SNode top = head->next;
head->next = head->next->next;
T e = top->element;
free(top);
return e;
}
//非递归实现
//先序遍历
void preOrder2(Node root) {
struct StackNode stack;
initStack(&stack);
//两个条件,只有当栈为空并且节点为NULL时才终止循环
while (root || !IsEmpty(&stack)) {
//先不断遍历左子树,直到没有为止
while (root) {
cout << root->element << " ";//然后打印当前节点的元素值
pushStack(&stack, root);//每遇到一个节点,就将节点入栈
root = root->left;//继续遍历下一个左孩子节点
}
Node node = popStack(&stack);//经过前边的遍历,明确左子树全部走完了,就进行右子树的遍历
//得到右孩子,如果有右孩子,下一轮会重复上面的步骤;如果没有右孩子,那么这里的root就会变成null,
// 下一轮开始会直接跳过上面的while,继续出栈下一个节点,再找右子树
root = node->right;
}
}
//中序遍历二叉树的非递归算法:没有让空指针进栈
void inOrder2(Node root) {
struct StackNode stack;
initStack(&stack);
//两个条件,只有当栈为空并且节点为NULL时才终止循环
while (root || !IsEmpty(&stack)) {
//先不断遍历左子树,直到没有为止
while (root) {
pushStack(&stack, root);//每遇到一个节点,就将节点入栈
root = root->left;//继续遍历下一个左孩子节点
}
Node node = popStack(&stack);//经过前边的遍历,明确左子树全部走完了,就进行右子树的遍历
cout << node->element << " ";//然后打印当前节点的元素值
//得到右孩子,如果有右孩子,下一轮会重复上面的步骤;如果没有右孩子,那么这里的root就会变成null,
// 下一轮开始会直接跳过上面的while,继续出栈下一个节点,再找右子树
root = node->right;
}
}
//中序遍历二叉树的非递归算法:让空指针进栈
void inOrder0(Node root) {
struct StackNode stack;
initStack(&stack);
T p;
pushStack(&stack, root);//根指针入栈
while (!IsEmpty(&stack)) {
//有栈顶元素 ,并且节点不为NULL
while ((p = peekStack(&stack)) && p) {
pushStack(&stack, p->left);//向左走到尽头
}
//直到左孩子为NULL,此时栈顶为整棵树最左边的节点,将NULL进栈,循环结束
//弹出栈顶空节点NULL ,因为子孩子为NULL,不需要打印值
p = popStack(&stack);//空指针退栈
if (!IsEmpty(&stack)) {//栈不为空,访问节点,向右一步
//弹出最上面的节点 ,也就是逻辑中序第一个节点
p = popStack(&stack);
cout << p->element << " ";
pushStack(&stack, p->right);
//如果有右孩子,则右孩子进栈,,接着以右孩子为逻辑根节点来中序遍历,判断右孩子是否有左孩子和右孩子....
//如果没有右孩子,就将NULL压进栈,下次循环会被弹出并不打印
}
}
}
//后序遍历
void postOrder2(Node root) {
struct StackNode stack;
initStack(&stack);
while (root || !IsEmpty(&stack)) {
while (root) {
pushStack(&stack, root);
root->flag = 0;//首次入栈,只能代表左子树遍历完成,所以设置flag为0
root = root->left;
}
root = peekStack(&stack);//获取节点
if (root->flag == 0) {//如果仅仅遍历左子树,那么flag就等于0
root->flag = 1;//此时标记为1表示遍历右子树
root = root->right;
}
else {
cout << root->element << " ";//当flag为1时,表示左右都遍历完成,这时再将值打印出来
popStack(&stack);//这时再把对应的节点出栈,因为左右都遍历完了
root = NULL;//置NULL,下一轮直接跳过while,然后继续取栈中剩余的节点,重复上述操作
}
}
}
//初始化对列
int initQueue(LinkedQueue queue) {
//设置头节点,并将队头和队尾同时指向头节点
QNode node = (QNode)malloc(sizeof(struct QueueNode));
if (node == NULL) return 0;
queue->front = queue->rear = node;
return true;
};
//入队
int offerQueue(LinkedQueue queue, T element) {
//入队,将新的节点入队放在队尾,并修改rear的指向
QNode node = (QNode)malloc(sizeof(struct QueueNode));
if (node == NULL) return 0;
node->element = element;
queue->rear->next = node;
queue->rear = node;
return true;
}
//判空
int isEmpty(LinkedQueue queue) {
//当队头和队尾指针同时指向同一个节点时,说明队列为空队列
return queue->front == queue->rear;
}
//出队
T pollQueue(LinkedQueue queue) {
//queue->front —— 头节点
//queue->front->next->element --队头结点中存储的节点的地址
T e = queue->front->next->element;
//queue->front->next --队头
QNode qNode = queue->front->next;
//更新链队列头节点
queue->front->next = queue->front->next->next;
//qNode=qNode->next;
//如果队列中只有一个节点,将队尾指针指向设置好的头节点
if (queue->rear == qNode) queue->rear = queue->front;
free(qNode);
//返回删除的旧的队头节点的节点地址,并没有物理删除,只是释放队列的节点空间
return e;
}
//层序遍历
void levelOrder(Node root) {
struct Queue queue;//创建队列
initQueue(&queue);
offerQueue(&queue, root);//先把根节点入队
while (!isEmpty(&queue)) {
Node node = pollQueue(&queue);
cout << node->element << " ";
if (node->left) //如果左、右孩子,依次将左、右孩子入队
offerQueue(&queue, node->left);
if (node->right)
offerQueue(&queue, node->right);
}
}
//求二叉树的深度
int getDepthTreeNode(Node root) {
if (root == NULL) {
return 0;
}
else {
int lLength = getDepthTreeNode(root->left);
int rlength = getDepthTreeNode(root->right);
int max = rlength > lLength ? (rlength + 1) : (lLength + 1);
return max;
}
};
Main.cpp
#include"MyBinaryTree.h"
int main() {
cout << "1--创建二叉树" << endl;
cout << "2--先序遍历二叉树【递归方式】" << endl;
cout << "3--中序遍历二叉树【递归方式】" << endl;
cout << "4--后序遍历二叉树【递归方式】" << endl;
cout << "5--先序遍历二叉树【非递归方式】" << endl;
cout << "6--中序遍历二叉树【非递归方式1】" << endl;
cout << "7--中序遍历二叉树【非递归方式2】" << endl;
cout << "8--后序遍历二叉树【非递归方式】" << endl;
cout << "9--层序遍历二叉树" << endl;
cout << "10--求二叉树的深度" << endl;
cout << "-1--退出" << endl;
int option;
Node t;//定义一个Node的指针
t = NULL;//不进行初识,就会报错
do {
cout << "请输入选择:";
cin >> option;
switch (option)
{
case 1:
cout << "请按先序输入二叉树中节点的值(一个字符)$字符表示空树:";
t = createBiTree(t);
if (t) {
cout << "创建二叉树成功!" << endl;
}
break;
case 2:
cout << "前序遍历【递归实现】:";
preOrder(t);
cout << endl;
break;
case 3:
cout << "中序遍历二叉树【递归方式】";
inOrder(t);
cout << endl;
break;
case 4:
cout << "后序遍历二叉树【递归方式】";
postOrder(t);
cout << endl;
break;
case 5:
cout << "先序遍历二叉树【非递归方式】";
preOrder2(t);
cout << endl;
break;
case 6:
cout << "中序遍历二叉树【非递归方式1】";
inOrder0(t);
cout << endl;
break;
case 7:
cout << "中序遍历二叉树【非递归方式2】";
inOrder2(t);
cout << endl;
break;
case 8:
cout << "后序遍历二叉树【非递归方式】";
postOrder2(t);
cout << endl;
break;
case 9:
cout << "层序遍历二叉树【非递归实现】";
levelOrder(t);
cout << endl;
break;
case 10:
cout << "二叉树的深度为:";
cout << getDepthTreeNode(t) << endl;
break;
case -1:
cout << "谢谢使用!再见!" << endl;
return 0;
default:
cout << "请输入正确的操作!";
break;
}
} while (option != -1);
}
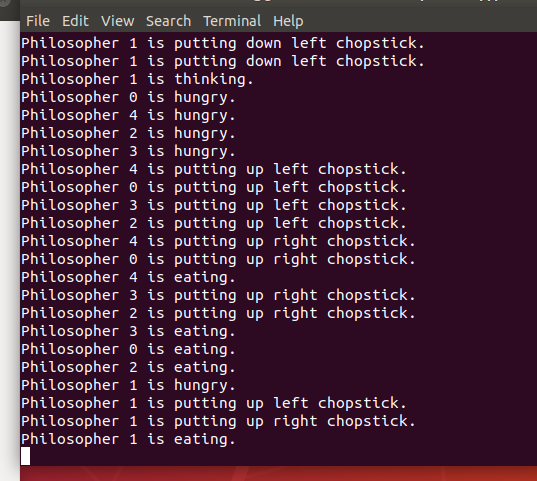
效果展示