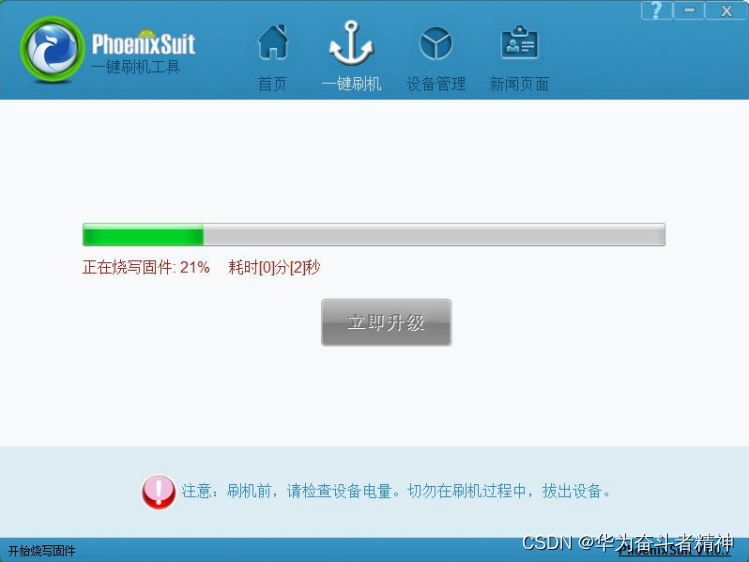
目录
- 1. 最小值和最大值
- 1.1 寻找最大值或最小值
- 1.2 同时寻找最大值与最小值
- 2. 期望为线性时间的选择算法
- 2.1 解决的问题
- 2.2 解决的办法
- 2.3 伪代码
- 2.4 RANDOMIZED-SELECT函数运行过程
- 2.5 算法时间复杂度的分析
- 2.5.1 最坏运行时间
- 2.5.2 期望运行时间
- 3. 最坏为线性时间的选择算法
- 3.1 算法思路
- 3.2 算法实现
- 3.2.1 PARTITION函数
- 3.2.2 SELECT函数
- 3.2.3 头文件
- 3.2.4 调用与传参
- 3.3时间复杂度分析
1. 最小值和最大值
1.1 寻找最大值或最小值
在有n个元素的集合中,要比较多少次才能确定其最小元素呢?我们可以很容易给出 n-1次比较这个上界,因为要确定最小值要将集合中的所有元素都要比较一遍。以下是在集合A中寻找最小值的伪代码:
MIMNIMUM(A)
min = A[1]
for i = 2 to A.length
if min > A[i]
min = A[i]
return min
寻找最大值只需对以上代码略微修改即可,比较次数也是至少为 n-1 次:
MAXIMUM(A)
max = A[1]
for i = 2 to A.length
if max < A[i]
max= A[i]
return max
1.2 同时寻找最大值与最小值
思路一:通过一次遍历数组分别比较每一个元素,更新最大值与最小值。
伪代码:
MAX-MIN(A)
min = A[1]
max = A[1]
for i = 2 to A.length
if min > A[i]
min = A[i]
if max < A[i]
max = A[i]
return (min,max)
通过伪代码可知对 n-1 个元素遍历一遍,每次比较2次,所以总共的比较次数为 ( n − 1 ) ∗ 2 ( n - 1) * 2 (n−1)∗2次。
思路二:
- 首先比较前两个元素,大的元素作为max初始值,小的元素作为min初始值。
- 然后将集合个数取半(m = n / 2),从 2 开始到 m 进行遍历,将 A[2i-1]与 A[2i]比较,选择其中大的值与 max 比较,并更新 max 的值,选择其中小的值与 min 比较,并更新 min 的值。
- 判断 n 是否等于2*m,若 n == 2*m 则证明n为偶数,在遍历中可以遍历到 n ,若 n !=m 则证明 n 为奇数,遍历过程中没有遍历到 n ,需要将 A[ n ]与 max 和 min 比较,得到最终的结果。
伪代码:
MAX-MIN (A)
// 比较前两个元素并为min与max初始化
if A[1] > A[2]
min = A[2]
max = A[1]
else
min = A[1]
max = A[2]
// 对剩下的 n-2 个数进行前后比较,并不断与min、max比较,更新min、max的值
m = n // 2
for i = 2 to m
if A[2i-1] > A[2i]
if A[2i] < min
min = A[2i]
if A[2i-1] > max
max = A[2i-1]
else
if A[2i-1] < min
min = A[2i-1]
if A[2i] > max
max = A[2i]
// 当n为奇数时,会剩余A[n]未参与比较,则要将其与最大值最小值进行比较
if n≠ 2m
if A[n] < min
min = A[n]
if A[n] > max
max = A[n]
return (min, max)
通过伪代码可知,比较次数有两种情况:
- 当 n 为奇数时,比较次数为
3
∗
(
n
−
1
)
/
2
3 * (n - 1) / 2
3∗(n−1)/2 次。
- 初识化: max 与 min 值比较 1 次。
- 中间过程:比较 3 ∗ ( n − 1 ) / 2 − 3 3 * (n - 1) / 2 - 3 3∗(n−1)/2−3次,因为要去掉开头的两个数比较所以要减 3。
- 最后:与 A[ n ] 比较 2 次。
- 总和: 1 + 3 ∗ ( n − 1 ) / 2 − 3 + 2 = 3 ∗ ( n − 1 ) / 2 1+ 3 * (n - 1) / 2 - 3 + 2 = 3 * (n - 1) / 2 1+3∗(n−1)/2−3+2=3∗(n−1)/2。
- 当 n 为偶数时,比较次数为
3
∗
n
/
2
−
2
3 * n / 2 - 2
3∗n/2−2 次。
- 初识化: max 与 min 值比较 1 次。
- 中间过程:比较 3 ∗ ( n − 1 ) / 2 − 3 3 * (n - 1) / 2 - 3 3∗(n−1)/2−3 次。
- 最后:不存在最后比较。
- 总和: 1 + 3 ∗ ( n − 1 ) / 2 − 3 = 3 ∗ ( n − 1 ) / 2 − 2 1+ 3 * (n - 1) / 2 - 3 = 3 * (n - 1) / 2 - 2 1+3∗(n−1)/2−3=3∗(n−1)/2−2。
无论是奇数还是偶数比较的次数为:
⌈
3
2
∗
n
⌉
−
2
\left\lceil\frac{3}{2}*n\right\rceil-2
⌈23∗n⌉−2
证明奇数次时比较次数满足上式:
3
2
∗
(
n
−
1
)
=
3
2
∗
n
−
3
2
=
3
2
∗
n
+
1
2
−
2
=
⌈
3
2
∗
n
⌉
−
2
\begin{aligned}\frac{3}{2}*(n-1)&=\frac{3}{2}*n-\frac{3}{2}\\&=\frac{3}{2}*n+\frac{1}{2}-2\\&=\left\lceil\frac{3}{2}*n\right\rceil-2\end{aligned}
23∗(n−1)=23∗n−23=23∗n+21−2=⌈23∗n⌉−2
2. 期望为线性时间的选择算法
2.1 解决的问题
在输入序列中,找到第 i 小的元素。
2.2 解决的办法
RANDOMIZD-SELECT,分治算法,与快速排序相同,仍然将输入的数组进行递归划分。但与快速排序不同的是,快速排序会递归处理划分的两边,而RANDOMIZED-SELECT只处理划分的一边,所以导致两者的执行性能会有差异。
2.3 伪代码
选择函数:
RANDOMIZED-SELECT(A,p,r,i)
1 if p == r
2 return A[p]
3 q = PARTITION(A,p,r) // 算法导论原文中是RANDOMIZED-PARTITION,其实差不多
4 k = q - p + 1
5 if i == k
6 return A[q]
7 else if i < k
8 return RANDOMIZED-SELECT(A,p,q-1,i)
9 else return RANDOMIZED-SELECT(A,q+1,r,i-k)
PARTITION函数:以 A[r] 为参考,执行结束后使得 A [ p . . . i ] ≤ A [ r ] A[p...i]\leq A[r] A[p...i]≤A[r], A [ r ] ≤ A [ i + 1... r ] A[r]\leq A[i+1...r] A[r]≤A[i+1...r],返回 A [ r ] A[r] A[r]的下标 i + 1 i+1 i+1。详见:PARTITION函数作用
PARTITION(A, p, r)
x = A[r]
i = p - 1
for j = p to r - 1
do if A[j] ≤ x
then i = i + 1
exchange A[i] with A[j]
exchange A[i + 1] with A[r]
return i + 1
2.4 RANDOMIZED-SELECT函数运行过程
- 第一行检查递归的基本情况,即 A [ p . . r ] A[p..r] A[p..r] 中只包括一个元素,在这种情况下 i i i 必然等于1,所以我们在第二行中将 A [ p ] A[p] A[p] 返回为第 i i i 小的元素。
- 其他情况下,调用第三行的 RANDOMIZED-PARTITON,将数组划分为两个子数组 A [ p . . q − 1 ] 和 A [ q + 1.. r ] A[p..q-1] 和 A[q+1..r] A[p..q−1]和A[q+1..r],使得 A [ p . . q − 1 ] A[p..q-1] A[p..q−1] 中的每一个元素都小于等于 A [ q ] A[q] A[q],而 A [ q ] A[q] A[q] 小于 A [ q + 1.. r ] A[q+1..r] A[q+1..r] 中的每一个元素。
- 计算 A [ q ] A[q] A[q] 在数组 A [ p . . r ] A[p..r] A[p..r] 中的位置 k k k,判断是否是第 i i i 小的元素,若刚好是,则返回 A [ q ] A[q] A[q],若不是,则继续往下执行。
- 若 i < k i<k i<k 则说明第 i i i 小的元素应该在 A [ p . . q − 1 ] A[p..q-1] A[p..q−1] 数组中,我们就在第八行对 A [ p . . q − 1 ] A[p..q-1] A[p..q−1] 数组进行递归调用: R A N D O M I Z E D − S E L E C T ( A , p , q − 1 , i ) RANDOMIZED-SELECT(A,p,q-1,i) RANDOMIZED−SELECT(A,p,q−1,i),此时全局的第 i i i 小仍是 A [ p . . q − 1 ] A[p..q-1] A[p..q−1] 数组中的第 i i i 小,所以我们传入 i i i 即可。
- 若 i ≥ k i\geq k i≥k 则说明第 i i i 小的元素应该在 A [ q + 1.. r ] A[q+1..r] A[q+1..r] 数组中,我们就在第九行对 A [ q + 1.. r ] A[q+1..r] A[q+1..r] 数组进行递归调用: R A N D O M I Z E D − S E L E C T ( A , q + 1 , r , i − k ) RANDOMIZED-SELECT(A,q+1,r,i-k) RANDOMIZED−SELECT(A,q+1,r,i−k),此时全局的第 i i i 小在 A [ q + 1.. r ] A[q+1..r] A[q+1..r] 数组中不是第 i i i 小了,而是第 i − k i - k i−k 小,所以我们要传入 i − k i - k i−k 。
- 如此递归我们终会得到答案。
2.5 算法时间复杂度的分析
2.5.1 最坏运行时间
RANDOMIZED-SELECT的最坏情况运行时间为 θ ( n 2 ) \theta(n^2) θ(n2),因为在每次划分时可能极不走运地总是按余下的元素中的最大的来进行划分,则需要划分 θ ( n ) \theta (n) θ(n) 的时间,而每一次划分操作又需要 θ ( n ) \theta(n) θ(n) 的时间,所以RANDOMIZED-SELECT需要 θ ( n 2 ) \theta(n^2) θ(n2) 的时间才能找到结果。
2.5.2 期望运行时间
为了分析RANDOMIZED-SELECT的期望运行时间,我们设该算法在一个含有
n
n
n 个元素的输入数组
A
[
p
.
.
r
]
A[p..r]
A[p..r] 上的运行时间是一个随机变量,记为
T
(
n
)
T(n)
T(n)。下面我们可以得到
E
[
T
(
n
)
]
E[T(n)]
E[T(n)] 的一个上界:程序 PARTITION 等概率的返回任何一个元素作为主元
(
A
[
q
]
)
(A[q])
(A[q]) 。因此对于每一个
k
(
1
≤
k
≤
n
)
k(1\leq k\leq n)
k(1≤k≤n),子数组
A
[
p
.
.
q
]
A[p..q]
A[p..q]有
k
k
k 个元素(全部小于或等于主元)的概率为
1
/
n
1/n
1/n。对所有
k
=
1
,
2
,
.
.
.
,
n
k=1,2,...,n
k=1,2,...,n 定义指示器随机变量
X
k
X_k
Xk 为:
X
k
=
I
{
子数组
A
[
p
.
.
q
]
正好包含
k
个元素
}
X_k = I\{子数组 A[p..q] 正好包含k个元素\}
Xk=I{子数组A[p..q]正好包含k个元素} 假设元素是互异的,则有:
E
[
X
k
]
=
1
/
n
E[X_k]=1/n
E[Xk]=1/n 当调用RANDOMIZED-SELECT并选择
A
[
q
]
A[q]
A[q] 作为主元时,事先并不知道是否会立即得到正确答案而结束,或者在子数组
A
[
p
.
.
q
−
1
]
A[p..q-1]
A[p..q−1]上递归,或者在
A
[
q
+
1..
r
]
A[q+1..r]
A[q+1..r] 上递归,这个取决于第
i
i
i 小的元素相对于
A
[
q
]
A[q]
A[q] 落在哪个位置,为了得到最大可能的输入数据递归调用所需时间,我们假定第
i
i
i 个元素总是在划分中包含元素较多的那一边,对于一个给定的RANDOMIZED-SELECT,指示器随机变量
X
i
X_i
Xi 恰好在给定的
k
k
k 值上取值为1,其他都是0,我们可能要递归处理两个子数组的大小分别为
k
−
1
k-1
k−1 和
n
−
k
n-k
n−k因此可以得到递归式:
T
(
n
)
≤
∑
k
=
1
n
X
k
∗
(
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
)
+
O
(
n
)
=
∑
k
=
1
n
X
k
∗
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
+
O
(
n
)
\begin{aligned}T(n)&\leq\sum_{k=1}^nX_k*(T(max(k-1,n-k)))+O(n)\\&=\sum_{k=1}^nX_k*T(max(k-1,n-k))+O(n) \end{aligned}
T(n)≤k=1∑nXk∗(T(max(k−1,n−k)))+O(n)=k=1∑nXk∗T(max(k−1,n−k))+O(n)
O
(
n
)
O(n)
O(n)为每一次的划分时间。
两边取期望值,得到:
E
[
T
(
n
)
]
≤
E
[
∑
k
=
1
n
X
k
∗
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
+
O
(
n
)
]
=
∑
k
=
1
n
E
[
X
k
∗
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
]
+
O
(
n
)
=
∑
k
=
1
n
E
[
X
k
]
∗
E
[
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
]
+
O
(
n
)
=
∑
k
=
1
n
1
n
∗
E
[
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
]
+
O
(
n
)
\begin{aligned}E[T(n)]&\leq E[\sum_{k=1}^nX_k*T(max(k-1,n-k))+O(n)] \\&=\sum_{k=1}^nE[X_k*T(max(k-1,n-k))]+O(n) \\&=\sum_{k=1}^nE[X_k]*E[T(max(k-1,n-k))]+O(n) \\&=\sum_{k=1}^n\frac{1}{n}*E[T(max(k-1,n-k))]+O(n) \end{aligned}
E[T(n)]≤E[k=1∑nXk∗T(max(k−1,n−k))+O(n)]=k=1∑nE[Xk∗T(max(k−1,n−k))]+O(n)=k=1∑nE[Xk]∗E[T(max(k−1,n−k))]+O(n)=k=1∑nn1∗E[T(max(k−1,n−k))]+O(n) 下面我们来考虑表达式
m
a
x
(
k
−
1
,
n
−
k
)
max(k-1,n-k)
max(k−1,n−k),有:
m
a
x
(
k
−
1
,
n
−
k
)
=
{
k
−
1
若
k
>
⌈
n
2
⌉
n
−
k
若
k
≤
⌈
n
2
⌉
max(k-1,n-k)=\begin{cases}k-1 &\text {若$k>\left \lceil \frac{n}{2} \right \rceil$ }\\n-k &\text {若$k \leq \left \lceil \frac{n}{2} \right \rceil$ }\end{cases}
max(k−1,n−k)={k−1n−k若k>⌈2n⌉ 若k≤⌈2n⌉ 如果
n
n
n 是偶数,则从
T
(
⌈
n
/
2
⌉
)
T(\lceil n/2 \rceil)
T(⌈n/2⌉) 到 T(n-1) 的每一项在总和中恰好出现两次。如果
n
n
n 是奇数,除了
T
(
⌊
n
/
2
⌋
)
T(\lfloor n/2 \rfloor)
T(⌊n/2⌋) 出现一次外,其他这些项也都会出现两次。因此我们有:
E
[
T
(
n
)
]
≤
2
n
∗
∑
k
=
⌊
n
/
2
⌋
n
−
1
E
[
T
(
k
)
]
+
O
(
n
)
E[T(n)] \leq \frac{2}{n}*\sum_{k=\lfloor n/2 \rfloor}^{n-1}E[T(k)]+O(n)
E[T(n)]≤n2∗k=⌊n/2⌋∑n−1E[T(k)]+O(n)我们将用替代法来得到
E
[
T
(
n
)
]
=
O
(
n
)
E[T(n)]=O(n)
E[T(n)]=O(n)。假设对满足这个递归式初始条件的某个常数
c
c
c,有
E
[
T
(
n
)
]
≤
c
n
E[T(n)]\leq cn
E[T(n)]≤cn。假设对小于某个常数的
n
n
n,有
T
(
n
)
=
O
(
1
)
T(n)=O(1)
T(n)=O(1)。同时还要选择一个常数
a
a
a,使得对所有的
n
>
0
n>0
n>0,上式中
O
(
n
)
O(n)
O(n)项所描述的函数(用来表示算法运行时间的非递归部分)由上界
a
n
an
an。利用这个归纳假设,可以得到
E
[
T
(
n
)
]
≤
2
n
∗
∑
k
=
⌊
n
/
2
⌋
n
−
1
E
[
T
(
k
)
]
+
O
(
n
)
=
2
c
n
(
∑
k
=
1
n
−
1
k
−
∑
k
=
1
⌊
n
/
2
⌋
−
1
k
)
+
a
n
=
2
c
n
(
(
n
−
1
)
n
2
−
(
⌊
n
/
2
⌋
−
1
)
⌊
n
/
2
⌋
2
)
+
a
n
≤
2
c
n
(
(
n
−
1
)
n
2
−
(
n
/
2
−
2
)
(
n
/
2
−
1
)
2
)
+
a
n
=
2
c
n
(
n
2
−
n
2
−
n
2
/
4
−
3
n
/
2
+
2
2
)
+
a
n
=
c
n
(
3
n
2
4
+
n
2
−
2
)
+
a
n
=
c
(
3
n
4
+
1
2
−
2
n
)
+
a
n
≤
3
c
n
4
+
c
2
+
a
n
=
c
n
−
(
c
n
4
−
c
2
−
a
n
)
\begin{aligned} E[T(n)]&\leq\frac{2}{n}*\sum_{k=\lfloor n/2 \rfloor}^{n-1}E[T(k)]+O(n) \\&=\frac{2c}{n}(\sum_{k=1}^{n-1}k-\sum_{k=1}^{\lfloor n/2 \rfloor-1}k)+an \\&=\frac{2c}{n}(\frac{(n-1)n}{2}-\frac{(\lfloor n/2 \rfloor-1)\lfloor n/2 \rfloor}{2})+an \\&\leq \frac{2c}{n}(\frac{(n-1)n}{2}-\frac{(n/2-2)(n/2-1)}{2})+an \\&=\frac{2c}{n}(\frac{n^2-n}{2}-\frac{n^2/4-3n/2+2}{2})+an \\&=\frac{c}{n}(\frac{3n^2}{4}+\frac{n}{2}-2)+an \\&=c(\frac{3n}{4}+\frac{1}{2}-\frac{2}{n})+an \\&\leq \frac{3cn}{4}+\frac{c}{2}+an \\&=cn-(\frac{cn}{4}-\frac{c}{2}-an) \end{aligned}
E[T(n)]≤n2∗k=⌊n/2⌋∑n−1E[T(k)]+O(n)=n2c(k=1∑n−1k−k=1∑⌊n/2⌋−1k)+an=n2c(2(n−1)n−2(⌊n/2⌋−1)⌊n/2⌋)+an≤n2c(2(n−1)n−2(n/2−2)(n/2−1))+an=n2c(2n2−n−2n2/4−3n/2+2)+an=nc(43n2+2n−2)+an=c(43n+21−n2)+an≤43cn+2c+an=cn−(4cn−2c−an)
为了完成证明,还需要证明:对足够大的
n
n
n,最后一个表达式至多是
c
n
cn
cn,等价的,
c
n
/
4
−
c
/
2
−
a
n
≥
0
cn/4-c/2-an\geq0
cn/4−c/2−an≥0。如果在上式两边加上
c
/
2
c/2
c/2,并且提取因子
n
n
n,就可以得到
n
(
c
/
4
−
a
)
≥
c
/
2
n(c/4-a)\geq c/2
n(c/4−a)≥c/2。只要我们选择的常数
c
c
c 能够满足
c
/
4
−
a
≥
0
c/4-a\geq 0
c/4−a≥0,即
c
≥
4
a
c\geq4a
c≥4a,就可以将两边同时除以
c
/
4
−
a
c/4-a
c/4−a,得到:
n
≥
c
/
2
c
/
4
−
a
=
2
c
c
−
4
a
n\geq\frac{c/2}{c/4-a}=\frac{2c}{c-4a}
n≥c/4−ac/2=c−4a2c因此,如果假设对所有
n
<
2
c
/
(
c
−
4
a
)
n<2c/(c-4a)
n<2c/(c−4a),都有
T
(
n
)
=
O
(
1
)
T(n)=O(1)
T(n)=O(1),那么就有
E
[
T
(
n
)
]
=
O
(
n
)
E[T(n)]=O(n)
E[T(n)]=O(n)。我们就可以得到这样的结论:假设所有元素是互异的,在期望线性时间内,我们可以找到任一顺序统计量,特别是中位数。
3. 最坏为线性时间的选择算法
3.1 算法思路
- 将输入的数组的 n 个元素划分为 ⌊ n / 5 ⌋ \lfloor n/5 \rfloor ⌊n/5⌋ 组,每组 5 个元素,且至多只有一组有剩下的 n mod 5 个元素组成。
- 寻找这 ⌈ n / 5 ⌉ \lceil n/5 \rceil ⌈n/5⌉ 组中每一组的中位数:首先对每组元素进行排序,然后去确定每组有序元素中的中位数。
- 对第二步中找出的 ⌈ n / 5 ⌉ \lceil n/5 \rceil ⌈n/5⌉ 个中位数,递归调用 SELECT 以找出其中的中位数 x x x (如果有偶数个中位数,为了方便约定 x x x 是较小的中位数)。
- 利用修改过的PARTITION函数,按中位数的中位数 x x x 对输入数组进行划分,并返回 x x x 在划分后数组中的下标 i。
- 如果
i
=
k
i=k
i=k,则直接返回
x
x
x。如果
i
<
k
i<k
i<k,则在低区递归调用SELECT函数来找第
i
i
i 小的元素。如果
i
>
k
i>k
i>k,则在高区递归调用SELECT函数来找第
n
−
i
n - i
n−i 小的元素。

3.2 算法实现
3.2.1 PARTITION函数
int PARTITION(vector<int>A, int p, int r, int median)
{
int x = median;
int i = p - 1;
for (int j = p; j <= r - 1; j++)
{
if (A[j] <= x)
{
i = i + 1;
swap(A[i], A[j]);
}
}
swap(A[i + 1], A[r]);
return i + 1;
}
3.2.2 SELECT函数
// 选择算法主函数
int select(vector<int>& nums, int left, int right, int k) {
if (left == right) // 如果只有一个元素,直接返回该元素
{
return nums[left];
}
int group_size = (right - left + 1) / 5; // 每组的大小为 (right - left + 1) / 5
vector<int> medians; // 用于存储每组中位数的向量
for (int i = 0; i < group_size; i++)
{
// 对每组元素进行排序,并找出中位数存入 medians 中
int start = left + i * 5; // 每组的起始下标
int end = min(start + 4, right); // 每组的结束下标,不超过 right
sort(nums.begin() + start, nums.begin() + end + 1); // 对每组元素进行排序
medians.push_back(nums[start + (end - start) / 2]); // 找出每组的中位数并存入 medians 中
}
int remaining = right - left - group_size * 5; // 剩余元素的个数
if (remaining > 0)
{
// 如果还有剩余元素,则对剩余元素进行排序,并找出中位数存入 medians 中
sort(nums.begin() + left + group_size * 5, nums.begin() + right + 1); // 对剩余元素进行排序
medians.push_back(nums[left + group_size * 5 + (remaining - 1) / 2]); // 找出剩余元素的中位数并存入 medians 中
}
int median_of_medians = select(medians, 0, medians.size() - 1, medians.size() / 2); // 递归调用 select 函数找出 medians 中的中位数
int pivot_index = PARTITION(nums, left, right, median_of_medians); // 根据 medianOfMedians 对 nums 进行分区,并返回分区点的下标
int pivot_rank = pivot_index - left + 1; // 分区点在 nums 中的排名
if (k == pivot_rank)
{
// 如果 k 等于分区点的排名,则直接返回分区点的元素值
return nums[pivot_index];
}
else if (k < pivot_rank)
{
// 如果 k 小于分区点的排名,则在左半部分递归调用 select 函数查找第 k 小的元素
return select(nums, left, pivot_index - 1, k);
}
else
{
// 如果 k 大于分区点的排名,则在右半部分递归调用 select 函数查找第 k-pivotRank 小的元素
return select(nums, pivot_index + 1, right, k - pivot_rank);
}
}
3.2.3 头文件
#include <iostream>
#include <vector>
#include <algorithm>
3.2.4 调用与传参
vector<int> nums = { 3, 2, 1, 5, 6, 4, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 }; // 给定的数组
int k = 13; // 要查找的第 k 小的元素的位置
int kthSmallest = select(nums, 0, nums.size() - 1, k);; // 调用 findKthSmallest 函数查找第 k 小的元素,并将结果赋值给 kthSmallest 变量
cout << "The " << k << "th smallest element is: " << kthSmallest << endl; // 输出结果
3.3时间复杂度分析

为了分析SELECT的运行时间,我们先要确定大于划分主元
x
x
x 的元素的个数的下界,在第二步找出的中位数中,至少有一半大于或等于中位数的中位数
x
′
x'
x′ 。因此,在这
⌈
n
/
5
⌉
\lceil n/5 \rceil
⌈n/5⌉ 个组中,除了当
n
n
n 不能被 5 整除时所产生的所含元素少于5 的那个组和包含
x
x
x 的那个组之外,至少有一半的组中有3个元素大于
x
x
x。不算这两个组,大于
x
x
x 的元素个数至少为:
3
(
⌈
1
2
⌈
n
5
⌉
⌉
−
2
)
≥
3
n
10
−
6
3(\left \lceil \frac{1}{2} \left \lceil \frac{n}{5} \right \rceil \right \rceil - 2) \geq\frac{3n}{10}-6
3(⌈21⌈5n⌉⌉−2)≥103n−6 所以说,至少有
3
n
/
10
−
6
3n/10-6
3n/10−6个元素小于
x
x
x。因此,在最坏的情况下,在第五步中,SELECT的递归调用最多用于
7
n
/
10
+
6
7n/10+6
7n/10+6个元素。
现在我们设计一个推导式来推导SELECT算法的最坏运行时间
T
(
n
)
T(n)
T(n)。步骤1、2和4需要
O
(
n
)
O(n)
O(n)的时间。(步骤2是对大小为 O(1) 的集合调用 O(n) 次插入排序。)步骤3所需时间为
T
(
⌈
n
/
5
⌉
)
T(\lceil n/5 \rceil)
T(⌈n/5⌉),步骤 5 所需时间至多为
T
(
7
n
/
10
+
6
)
T(7n/10+6)
T(7n/10+6)。
我们假设T是单调递增的,假设任何少于140个元素的输入需要
O
(
1
)
O(1)
O(1)时间,根据如上假设我们可以得到如下递归式:
T
(
n
)
≤
{
O
(
1
)
若
n
<
140
T
(
⌈
n
/
5
⌉
)
+
T
(
7
n
/
10
+
6
)
+
O
(
n
)
若
n
≥
140
T(n)\leq \begin{cases}O(1) &\text {若$n<140$ }\\T(\lceil n/5 \rceil)+T(7n/10+6)+O(n) &\text {若$n \geq 140$ }\end{cases}
T(n)≤{O(1)T(⌈n/5⌉)+T(7n/10+6)+O(n)若n<140 若n≥140 我们用替换法来证明这个运行时间是线性的。我们将证明对某个适当大的常数c和所有的
n
>
0
n>0
n>0,有
T
(
n
)
≤
c
n
T(n)\leq cn
T(n)≤cn。首先,假设对某个适当大的常数 c 和所有的
n
<
140
n<140
n<140,有
T
(
n
)
≤
c
n
T(n) \leq cn
T(n)≤cn;如果 c 足够大,这个假设显然成立。同时还要挑选一个常数 a ,使得对所有的
n
>
0
n>0
n>0,上述公式的
O
(
n
)
O(n)
O(n)像所对应的函数(用来描述算法运行时间中的非递归部分)有上界
a
n
an
an.将这个归纳假设带入上述递归式的右边,得到:
T
(
n
)
≤
c
⌈
n
/
5
⌉
+
c
(
7
n
/
10
+
6
)
+
a
n
=
c
n
/
5
+
c
+
7
c
n
/
10
+
6
c
+
a
n
=
9
c
n
/
10
+
7
c
+
a
n
=
c
n
+
(
−
c
n
/
10
+
7
c
+
a
n
)
(1)
\begin{aligned} T(n) &\leq c \lceil n/5 \rceil + c(7n/10+6) + an \\&=cn/5+c+7cn/10+6c+an \\&=9cn/10+7c+an \\&=cn+(-cn/10+7c+an) \tag{1} \end{aligned}
T(n)≤c⌈n/5⌉+c(7n/10+6)+an=cn/5+c+7cn/10+6c+an=9cn/10+7c+an=cn+(−cn/10+7c+an)(1)如果下式成立,上式 (1) 最多是
c
n
cn
cn:
−
c
n
/
10
+
7
c
+
a
n
≤
0
(2)
-cn/10+7c+an\leq 0 \tag{2}
−cn/10+7c+an≤0(2)
当 n > 70 n>70 n>70 时上式 (2) 等价于不等式 c ≥ 10 a ( n / ( n − 70 ) ) c\geq 10a(n/(n-70)) c≥10a(n/(n−70)) 。因为假设 n > 140 n>140 n>140 ,所以有 n ( n − 70 ) ≤ 2 n(n-70) \leq 2 n(n−70)≤2。因此选择 c ≥ 20 a c\geq 20a c≥20a 就能满足以上不等式(2)。(注意,这里的常数140并没有什么特别之处,我们可以用任何严格大于70的整数来替换它,然后在相应的选择c即可。)因此,最坏情况下SELECT的运行时间是线性的。