动态规划步骤

1、状态表示

是什么：dp表（可能是一维或二维数组）里的值所表示的含义。

怎么来：

1、题目要求

2、经验+题目要求

3、发现重复子问题

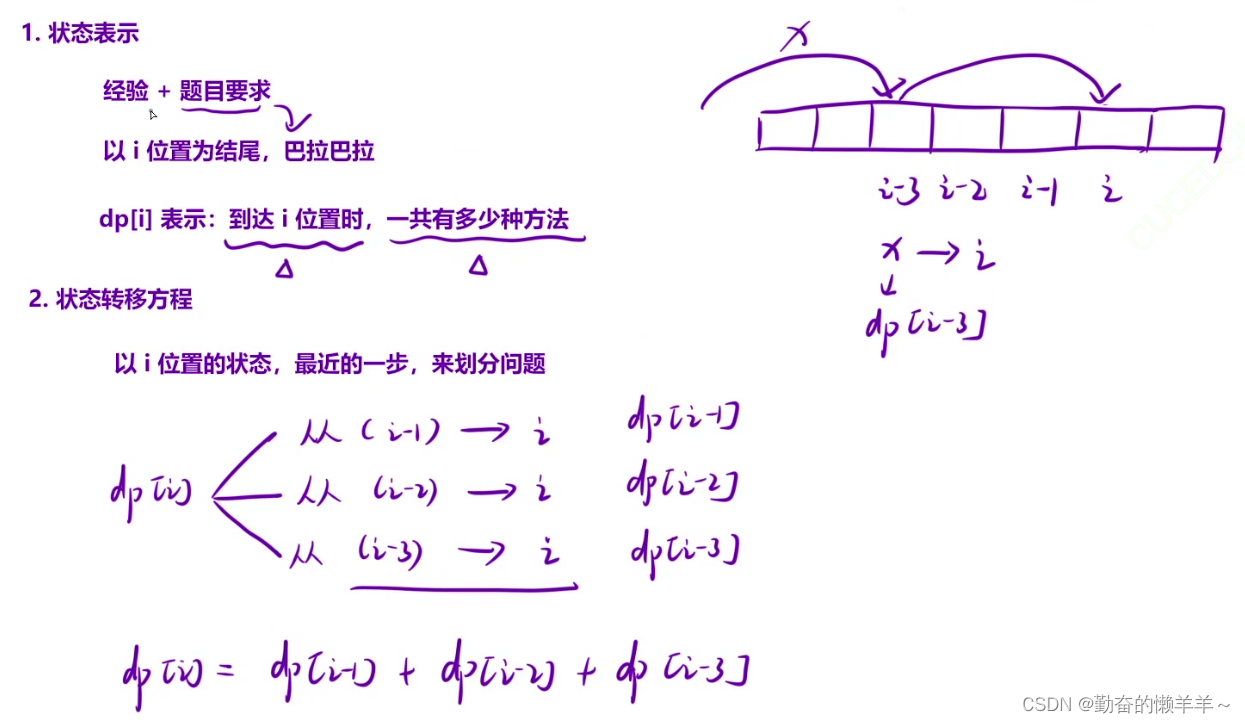
2、状态转移方程

dp[i]=...

3、初始化

保证填表不越界

4、填表顺序

5、返回值

写代码时，可以就按一下步骤：

1、创建dp表

2、初始化

3、填表

4、返回值 

5、可能会需要处理边界

一、第n个泰波那契数

 

class Solution {
public:
    int tribonacci(int n) {
        vector<int> dp(n+1);

        if(n==0) return 0;
        if(n==1||n==2) return 1;

        dp[0] = 0,dp[1] = 1,dp[2] = 1;

        for(int i = 3;i <= n;i++){
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
        }
        
        return dp[n];
    }
};

空间优化------滚动数组

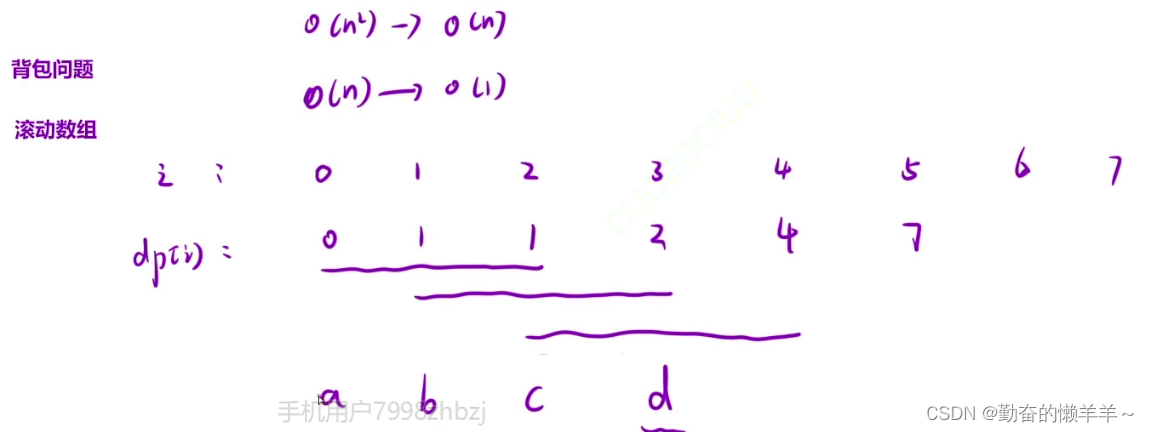
将abcd向后平移。 

class Solution {
public:
    int tribonacci(int n) {

        if(n==0) return 0;
        if(n==1||n==2) return 1;

        int a = 0,b = 1,c = 1,d;

        for(int i = 3;i <= n;i++){
            d = a+b+c;
            a = b;
            b = c;
            c = d;
        }
        
        return d;
    }
};

二、三步问题 

 

取模问题：每做一次加法就要做一次取模

class Solution {
public:
    int waysToStep(int n) {
        vector<int> dp(n+1);
        const int MOD = 1e9+7;
        if(n == 1||n == 2) return n;
        if(n == 3) return 4;

        dp[1] = 1,dp[2] = 2,dp[3] = 4;

        for(int i = 4;i <= n;i++){
            dp[i] = ((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;
        }
        return dp[n];
    }
};

三、最小花费爬楼梯

注意：楼顶是最后一个台阶的下一个位置。

 

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n = cost.size();
        vector<int> dp(n + 1);
        dp[0] = dp[1] = 0;
        for(int i = 2;i <= n;i++){
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[n];
    }
};

 四、解码方法

 注意：dp[i-1]和dp[i-2]是解密成功才加的。

优化版初始化（更好处理边界）

把数组统一往后移一位，开多一位 。

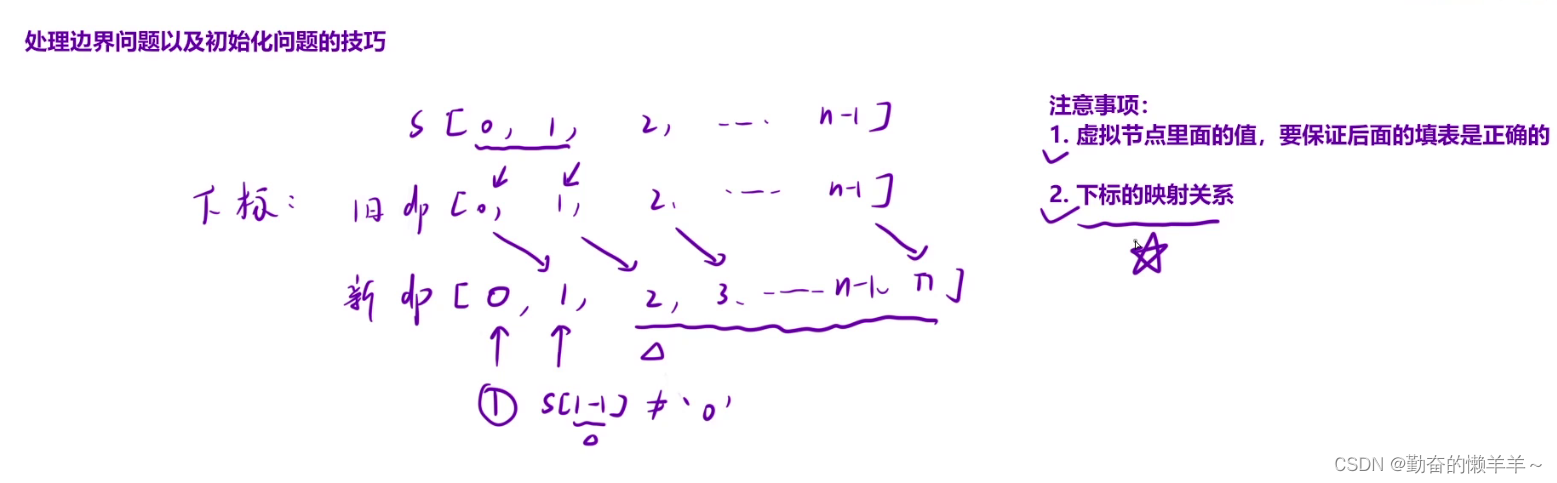
class Solution {
public:
    int numDecodings(string s) {
        int n = s.size();
        vector<int> dp(n + 1);
        dp[0] = 1;
        dp[1] = s[0] != '0';


        for(int i = 2;i <= n;i++){
            if(s[i-1] != '0') dp[i] += dp[i-1];
            int t = (s[i-2]-'0')*10 + s[i-1]-'0';
            if(t <= 26 && t >= 10) dp[i] += dp[i-2];           
        }
        return dp[n];
    }
};