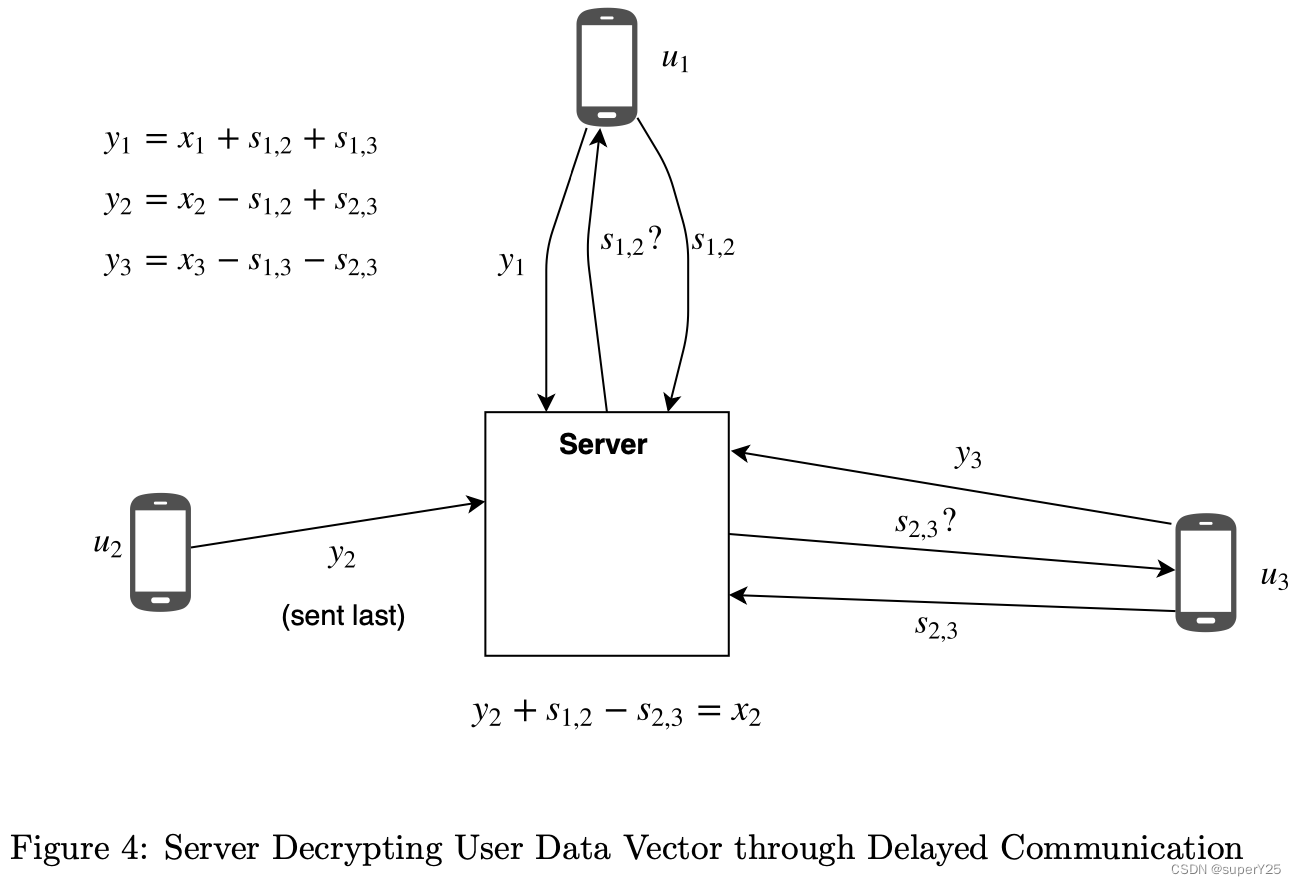
很喜欢《水浒传》，希望能将它融入我的考研复习中，打算用水浒传数据来贯穿数据结构的各种知识，先汇总下找到的数据集

• 天池上看到的一个水浒传文本数据集：https://tianchi.aliyun.com/dataset/36027

• Hareric/masterworkNLP: 基于社区检测的名著分析—以《水浒传》为例 ，这个项目的data文件夹里面有人物名字和绰号的对应文件，还有水浒传的文本数据

• HO-UN/-Word-frequency-statistics-and-character-analysis: 水浒传词频统计和人物性格分析，这里面有词频统计，还有原文本数据

• 用知识图谱打开梁山好汉一百单八将_csdn108位梁山好汉,都有各自的粉丝。从键盘上读入一组粉丝喜好梁山好汉的名字(_PKUMOD的博客)

  • 他们把数据集分享到这里了http://file.gstore.cn/f/bd6676d4b3ea452f8fbc/?dl=1

• zrhcode/KGQA_SHZ: 基于Neo4j的《水浒传》人物关系可视化及问答系统 (github.com)

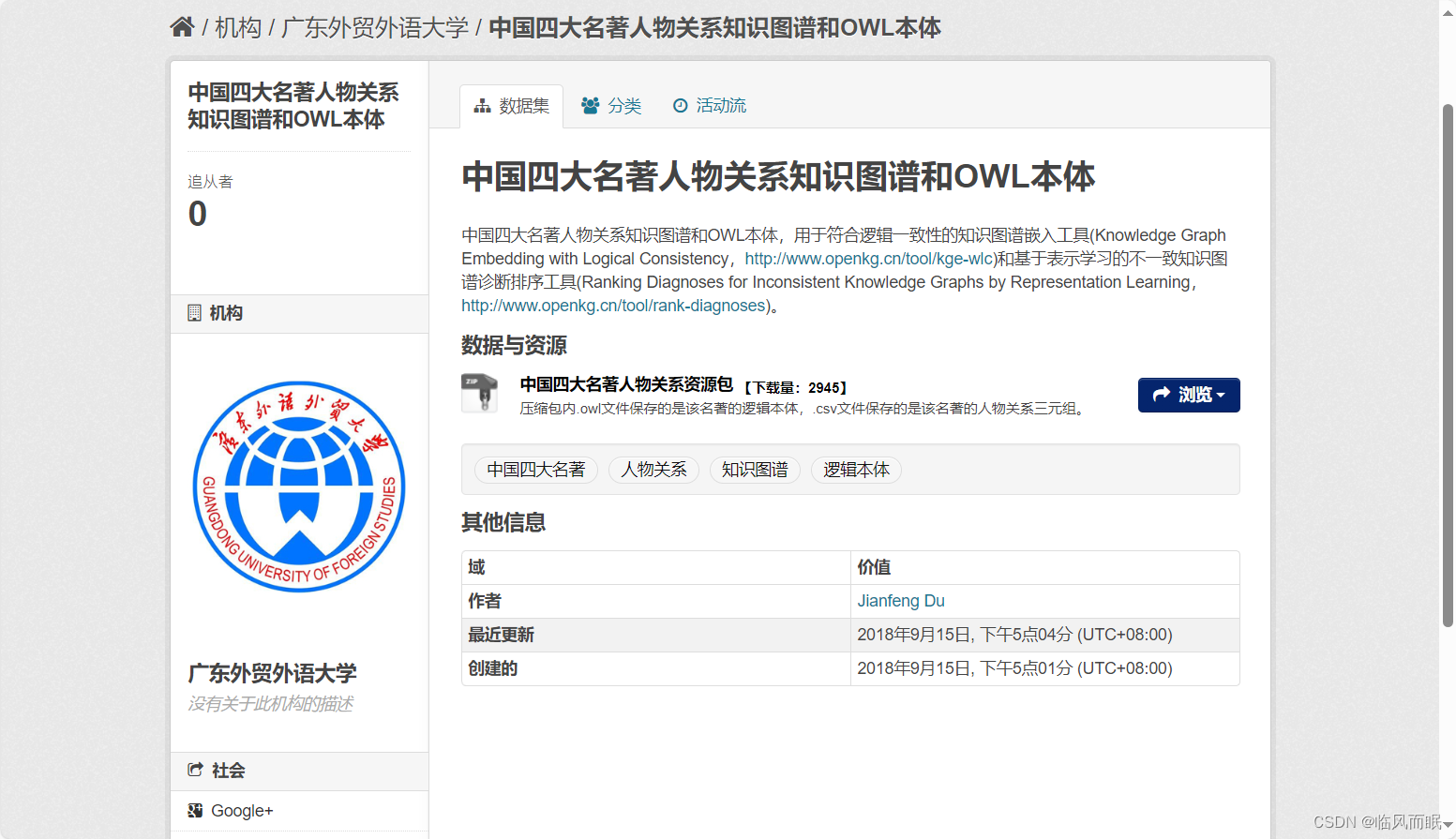
• 还有openKg上面，有很多不错的数据集，其中也有四大名著的
  

• 和鲸平台也看到两个

  • 一个是B站水浒传播放的数据集
  • 还有一个是水浒传人物出场顺序及简介的数据集

下面这些不是数据集，但是很有意思哈哈

• 【学习】趣味数据挖掘——借水浒传故事，释决策树思路-腾讯云开发者社区-腾讯云
• [白话解析] 以水浒传为例深入浅出最大熵模型-CSDN博客