存在负权边的单源最短路径的原理和C++实现

news2024/11/16 1:18:06

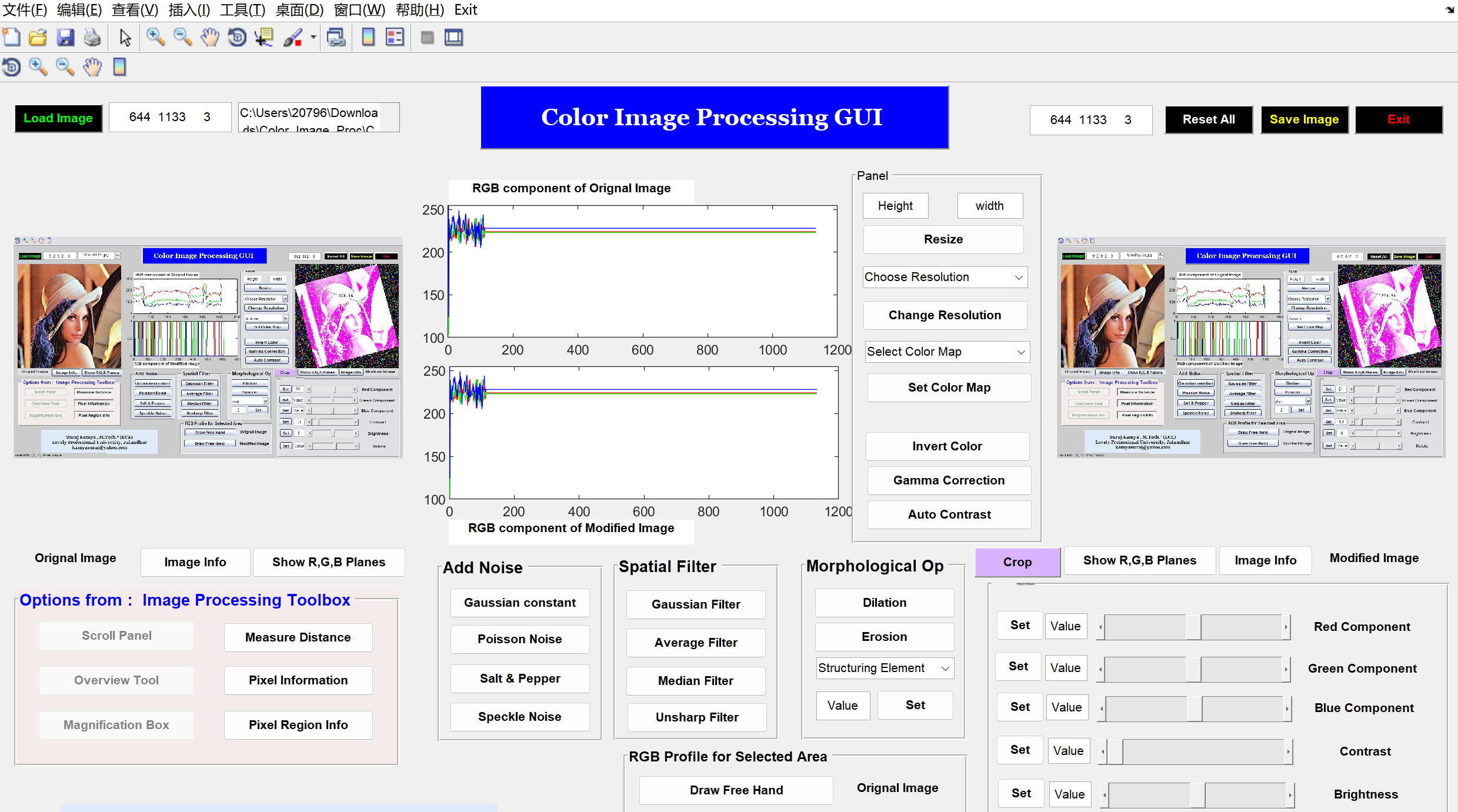
负权图

此图用朴素迪氏或堆优化迪氏都会出错，floyd可以处理。

负环图

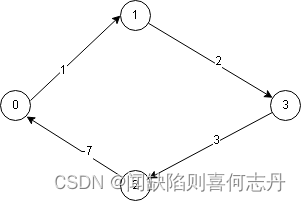
但floyd无法处理负权环，最短距离是无穷小。在环上不断循环。

经过k条边的最短距离（可能有负权变）

贝尔曼福特算法(bellman_ford)就是解决此问题的。

原理

循环k次，循环第i次时，m_vDis表示各点最多经过i-1条边的最短距离；vDis表示各点最多经过i条边的最短距离。

核心代码

template<const int INF=1000*1000*1000>
class CBellMan
{
public:
CBellMan(int n, const vector<vector<int>>& edges,int s , int k )
{
m_vDis.assign(n, INF);
m_vDis[s] = 0;
for (int i = 1; i <= k; i++)
{
vector<int> curDis = m_vDis;
for (const auto& v : edges)
{
if (INF == m_vDis[v[0]])
{
continue;
}
curDis[v[1]] = min(curDis[v[1]], m_vDis[v[0]] + v[2]);
}
m_vDis.swap(curDis);
}
}
vector<int> m_vDis;
};

测试样例

#include <vector>
#include<assert.h>
using namespace std;

int main()
{
const int INF = 1000 * 1000 * 1000;
vector<vector<int>> edges = { {0,1,1},{1,2,2},{2,3,3},{3,0,-7} };
vector<vector<int>> results = { {0,INF,INF,INF},{0,1,INF,INF},{0,1,3,INF},{0,1,3,6},{-1,1,3,6},{-1,0,3,6},{-1,0,2,6},{-1,0,2,5},{-2,0,2,5} };
for (int i = 0; i < results.size(); i++)
{
CBellMan<> bm(4, edges, 0, i);
for (int j = 0; j < 4; j++)
{
assert(bm.m_vDis[j] == results[i][j]);
}
}
}

最短路径

最短路径就是经过“点数-1”条边的最短路径。如果没环，这些边可以到达任意点。如果有正权环和0权环，则拿掉这个环。如果负权环，则最小距离是无穷小。下面来检测负权环。循环“点数-1”后，再循环一次，如果有点的最短距离变小，则一定有负权环；没负权环，不会变短。如果有负权环，则再循环一次，一定有点（任意负权环的负权边的终点）距离变短。假定此点是e，拿掉负权环上所有的边后，源点到e的最短路径为Path。不拿掉负权环，则e的最短路径为:Path+此负权环。

核心代码

template<const int INF=1000*1000*1000>
class CBellMan
{
public:
CBellMan(int n, const vector<vector<int>>& edges,int s , int k )
{
m_vDis.assign(n, INF);
m_vDis[s] = 0;
for (int i = 1; i <= k; i++)
{
vector<int> curDis = m_vDis;
Do(edges, curDis);
m_vDis.swap(curDis);
}
}
bool Check(const vector<vector<int>>& edges)
{
vector<int> curDis = m_vDis;
Do(edges, curDis);
for (int i = 0; i < curDis.size(); i++)
{
if (m_vDis[i] != curDis[i])
{
return true;
}
}
return false;
}
void Do(const std::vector<std::vector<int>>& edges, std::vector<int>& curDis)
{
for (const auto& v : edges)
{
if (INF == m_vDis[v[0]])
{
continue;
}
curDis[v[1]] = min(curDis[v[1]], m_vDis[v[0]] + v[2]);
}
}
vector<int> m_vDis;
};

测试样例

#include <vector>
#include<assert.h>
#include "BellMan.h"
using namespace std;

void Test1()
{
const int INF = 1000 * 1000 * 1000;
vector<vector<int>> edges = { { 0,1,1 },{ 1,2,2 },{ 2,3,3 },{ 3,0,-7 } };
vector<vector<int>> results = { { 0,INF,INF,INF },{ 0,1,INF,INF },{ 0,1,3,INF },{ 0,1,3,6 },{ -1,1,3,6 },{ -1,0,3,6 },{ -1,0,2,6 },{ -1,0,2,5 },{ -2,0,2,5 } };
for (int i = 0; i < results.size(); i++)
{
CBellMan<> bm(4, edges, 0, i);
for (int j = 0; j < 4; j++)
{
assert(bm.m_vDis[j] == results[i][j]);
}
}
}

void Test2()
{
const int INF = 1000 * 1000 * 1000;
vector<vector<int>> edges = { { 0,1,1 },{ 1,2,2 },{ 2,3,3 },{ 3,0,-7 } };
vector<int> results = { false,false,true };
for (int i = 0; i < 3; i++)
{
edges[3][2] = -5 - i;
CBellMan<> bm(4, edges, 0, 3);
assert(results[i] == bm.Check(edges));
}
}
int main()
{
Test1();
Test2();
}