背景
机器学习模型对数据的分析具有很大的优势,很多敏感数据分布在用户各自的终端。若大规模收集用户的敏感数据具有泄露的风险。
对于安全分析的一般背景就是认为有n方有敏感数据,并且不愿意分享他们的数据,但可以分享聚合计算后的结果。
联邦学习是一种训练数据在多方训练,然后聚合结果得到最终的中心化模型。其中的关键就是多方结果的安全聚合。
风险模型
有很多用户,假设用户都是诚实但好奇的,即会遵守协议规则,但会通过拼凑数据获取敏感信息。换句话说就是恶意的,很可能执行不好的行为。
安全聚合
问题的定义、目标和假设
风险模型假设用户和中心服务器都是诚实且好奇的。如果用户是恶意的,他们有能力在不被监测的情况下影响聚合结果。
安全聚合协议:
- 操作高维向量;
- 不管计算中涉及到的用户子集,通信是高效的;
- 用户dropout是robust;
- 足够安全
第一次尝试:一次填充掩码
对于所有的用户,通过每个用户对
u
,
v
u,v
u,v构建一个secret,具体逻辑:对所有用户进行排序,当用户
u
<
v
u < v
u<v构建一个
+
s
u
,
v
+s_{u,v}
+su,v,相反则构建一个
−
s
v
,
u
-s_{v,u}
−sv,u,如下图:
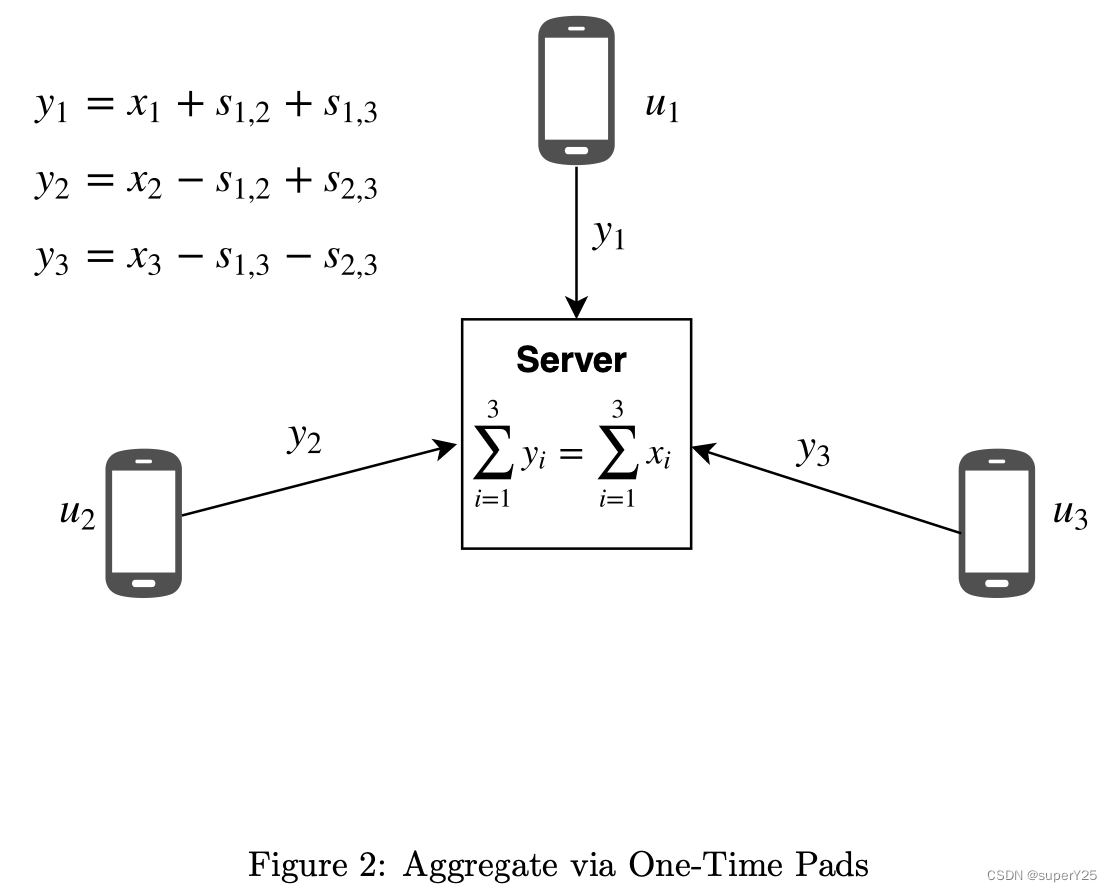
当聚合的时候
∑
i
=
1
3
=
x
1
+
s
1
,
2
+
s
1
,
3
+
x
2
−
s
1
,
2
+
s
2
,
3
+
x
3
−
s
1
,
3
−
s
2
,
3
\sum_{i=1}^3=x_1+s_{1,2}+s_{1,3}+x_2-s_{1,2}+s_{2,3}+x_3-s_{1,3}-s_{2,3}
i=1∑3=x1+s1,2+s1,3+x2−s1,2+s2,3+x3−s1,3−s2,3
缺点:
- 二次通信,每个用户对 u , v u, v u,v都需要产生他们的秘钥 s u , v s_{u,v} su,v
- 如果任何一个用户drop out,对于 ∑ ∀ i y i \sum_{\forall i}y_i ∑∀iyi都会变成垃圾数据,从而本次不能聚合。
利用Diffie-Hellman秘钥交换改进二次通信
所有的用户商定一个大素数
p
p
p和一个基本数
g
g
g。用户将自己的公钥(
g
a
u
m
o
d
p
g^{a_{u}} \mod p
gaumodp,其中
a
u
a_u
au是用户的秘钥)发送给server,然后server广播一个公钥给其他的用户,其他用户使用自己的秘钥和该公钥进行计算,如:
u
1
:
(
g
a
2
)
a
1
m
o
d
p
=
g
a
1
a
2
m
o
d
p
=
s
1
,
2
u_1:(g^{a_2})^{a_1}\quad mod \quad p = g^{a_1a_2}\quad mod \quad p=s_{1,2}
u1:(ga2)a1modp=ga1a2modp=s1,2
u
2
:
(
g
a
1
)
a
2
m
o
d
p
=
g
a
1
a
2
m
o
d
p
=
s
1
,
2
u_2:(g^{a_1})^{a_2}\quad mod \quad p = g^{a_1a_2}\quad mod \quad p=s_{1,2}
u2:(ga1)a2modp=ga1a2modp=s1,2
Diffie-Hellman秘钥交换比上面的方法更简单、更高效。
第二次尝试:可恢复的一次性填充掩码
同上述方法类似,用户将他们加密后的向量
y
u
y_u
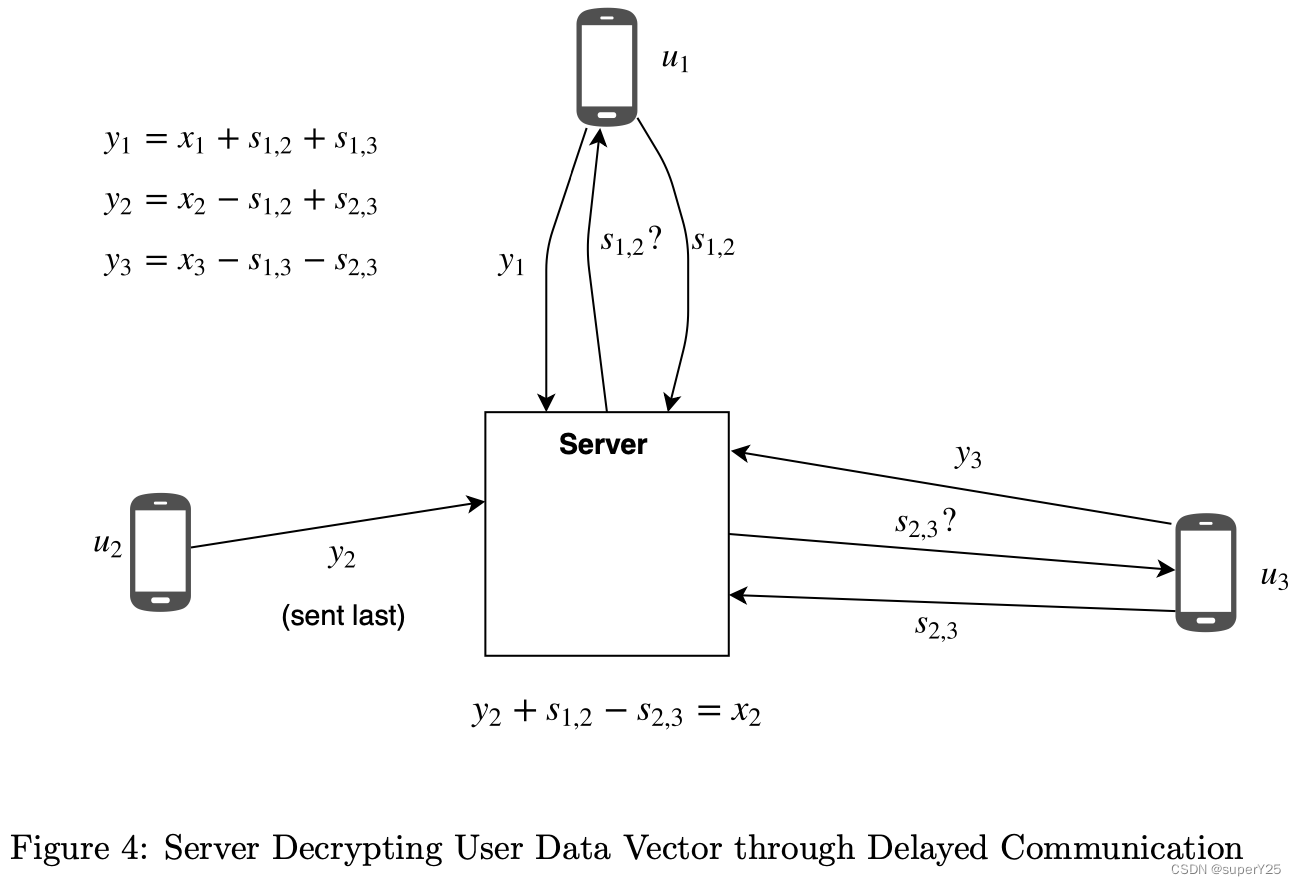
yu发给server,然后server询问其他用户是否包含drop out的用户,是的话则取消他们的秘密绑定。如下图: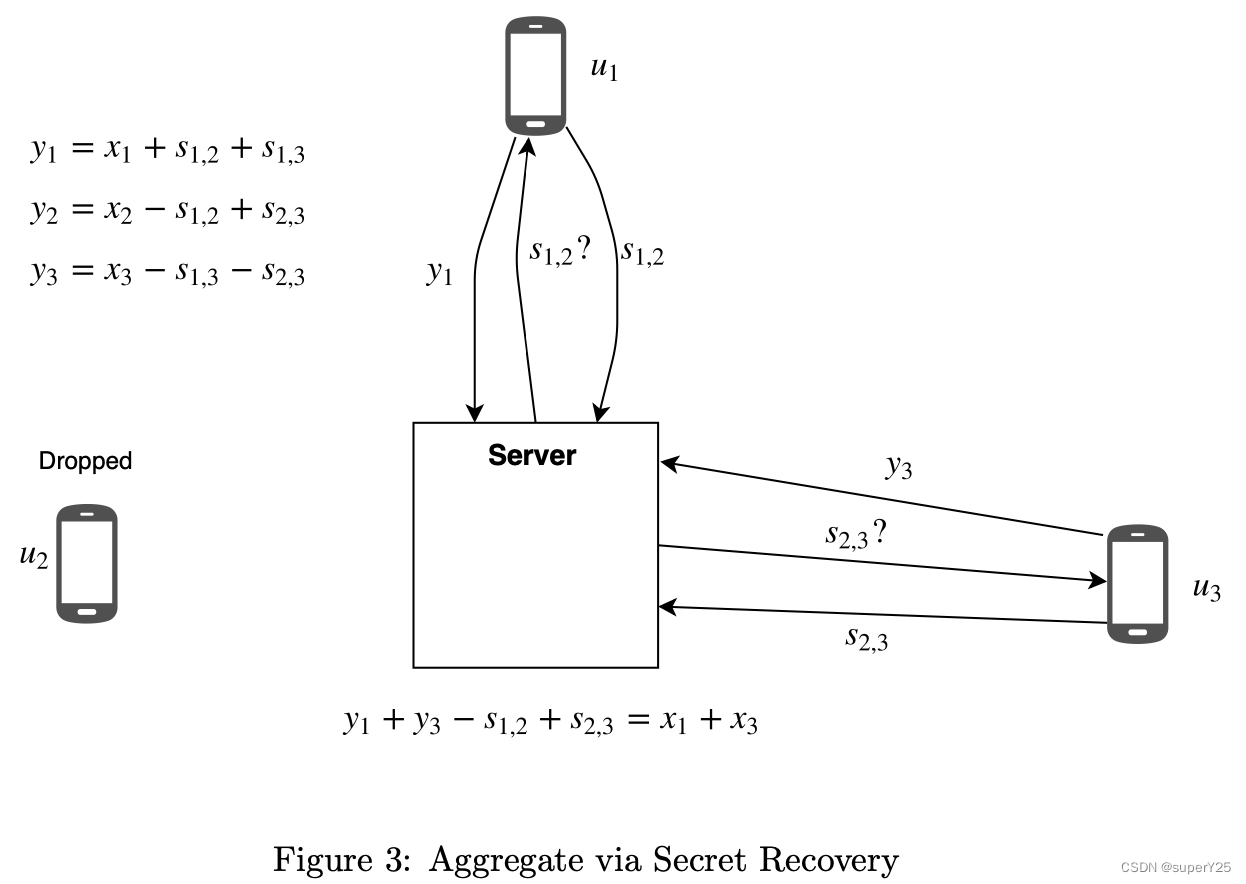
该方法的缺点:
- 在recovery阶段发生额外的用户drop out,这将要求新drop out的用户也需要recovery,在大量用户的情况下,轮询次数将增加。
- 通信延迟导致server以为用户被drop out。因此,会想其他用户recovery秘钥,这导致server在接收到该用户的secret时,解密该用户的 x u x_u xu。如下图
因此,如果server是恶意的,则可以通过此方法获取用户的inputs。
Shamir秘密分享:
允许一个用户将秘密 s s s分享成 n n n个shares,然后任意 t t t个shares都能重构出秘密 s s s,而任意 t − 1 t-1 t−1个shares都不能重构出秘密 s s s。
第三次尝试:处理Dropped用户
为了克服在通信轮次之间,新dropped用户增加recovery阶段,用户Shamir秘密分享的阈值。每个用户发送他们DH秘钥的shares给其他用户,只要符合阈值条件,允许pairwise secrets被recovered,即使是recovery期间新dropped用户。协议可以总结如下:
- 每个用户 u u u将他的DH秘钥 a u a_u au分享成n-1个部分 a u 1 , a u 2 , . . , a u ( n − 1 ) a_{u1},a_{u2},..,a_{u(n-1)} au1,au2,..,au(n−1),并发送给其他 n − 1 n-1 n−1个用户。
- server接收来自在线用户的 y u y_u yu(记为: U o n l i n e , r o u n d 1 U_{online,round 1} Uonline,round1)。
- server计算dropped用户集,表示为 U d r o p p e d , r o u n d 1 U_{dropped,round 1} Udropped,round1
- server向 U o n l i n e , r o u n d 1 U_{online,round 1} Uonline,round1询问 U d r o p p e d , r o u n d 1 U_{dropped,round 1} Udropped,round1的shares。在第二轮通信中假设至少还有t个用户在线。
- server对 U d r o p p e d , r o u n d 1 U_{dropped,round 1} Udropped,round1的秘钥进行recover,并在最后聚合时,remove掉他们。
该方法依然没有解决恶意server因为通信延迟问题获取用户的数据问题。
最后一次尝试:双重掩码
双重掩码的目标就是为了防止用户数据的泄露,即使当server重构出用户的masks。首先,每个用户产生一个额外的随机秘钥
a
u
a_u
au,并且分布他的shares给其他的用户。生成
y
u
y_u
yu时,添加第二重mask:
y
u
=
x
u
+
a
u
+
∑
u
<
v
s
u
,
v
−
∑
u
>
v
s
v
,
u
m
o
d
e
R
y_u = x_u+a_u+\sum_{u<v}s_{u,v}-\sum_{u>v}s_{v,u}\quad mode \quad R
yu=xu+au+u<v∑su,v−u>v∑sv,umodeR
在recovery轮次中,对于每个用户,server必须作出精确的选择。从每个在线的成员
v
v
v中,请求
u
u
u的
s
u
,
v
s_{u,v}
su,v或者
a
u
a_u
au。对于同一个用户,一个诚实的
v
v
v通过这两种shares不能还原数据,server需要从所有dropped的用户中聚合至少t个
s
u
,
v
s_{u,v}
su,v的shares或者所有在线用户中t个
a
u
a_u
au的shares。之后,server便可以减去剩余的masks还原数据。
该方法整个过程中的计算和通信数量级还是
n
2
n_2
n2,n表示参与计算的用户数。一个新的问题:当
t
<
n
2
t<\frac{n}{2}
t<2n时,server可以分别询问用户的
s
u
,
v
s_{u,v}
su,v和
a
u
a_u
au,来解密用户的数据。
参考文献:
[1] K. Bonawitz. ”Practical Secure Aggregation for Privacy-Preserving Machine Learning”. 2017.
[2] J. Konecny. ”Federated Learning: Strategies for Improving Communication Efficiency”. 2017.
[3] H. B. McMahan. ”Communication-Efficient Learning of Deep Networks from Decentralized Data”. 2016.
[4] A. Shamir. ”How to Share a Secret”. 1979.



![【洛谷 P1216】[USACO1.5] [IOI1994]数字三角形 Number Triangles 题解(动态规划)](https://img-blog.csdnimg.cn/img_convert/eeccc0b0b79c371c799c3d759284b7ad.png)