废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是螺旋矩阵,使用【二维数组】这个基本的数据结构来实现
二分查找【EASY】
从最简单的二分查找入手,进而开始解决一系列其变体问题
题干
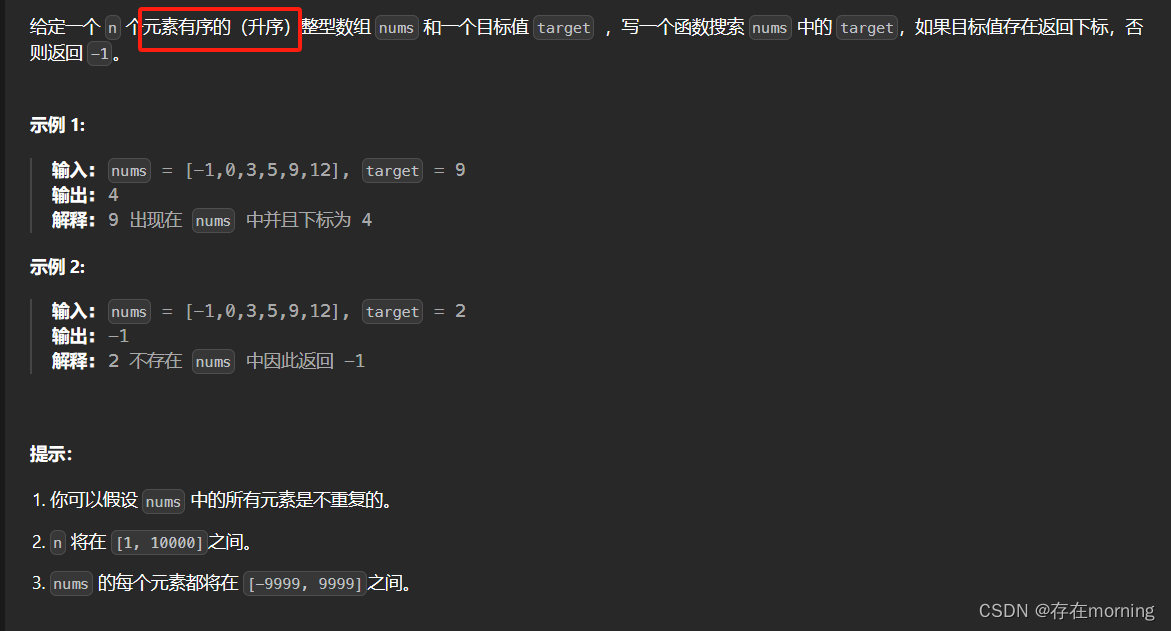
解题思路
循序渐进的理解关于二分查找的一些细节,
1 二分查找框架代码
int binarySearch(int[] nums, int target) {
int left = 0, right = ...;
while(...) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
...
} else if (nums[mid] < target) {
left = ...
} else if (nums[mid] > target) {
right = ...
}
}
return ...;
}
分析二分查找的一个技巧是:不要出现 else,而是把所有情况用 else if 写清楚,这样可以清楚地展现所有细节,其中 ... 标记的部分,就是可能出现细节问题的地方,当你见到一个二分查找的代码时,首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。
另外声明一下,计算 mid 时需要防止溢出,代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同,但是有效防止了 left 和 right 太大直接相加导致溢出
2 最基本的二分查找
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
为什么 while 循环的条件中是 <=,而不是 <
因为初始化 right 的赋值是 nums.length - 1,即最后一个元素的索引,而不是 nums.length
3 二分查找变体:找重复元素的左右边界
来梳理一下这些细节差异的因果逻辑:
第一个,最基本的二分查找算法:
因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1
因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回
第二个,寻找左侧边界的二分查找:
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界
第三个,寻找右侧边界的二分查找:
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界
又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right,必须减一
对于寻找左右边界的二分搜索,常见的手法是使用左闭右开的「搜索区间」,我们还根据逻辑将「搜索区间」全都统一成了两端都闭,便于记忆,只要修改两处即可变化出三种写法:
int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
// 最后要检查 left 越界的情况
if (left >= nums.length || nums[left] != target)
return -1;
return left;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
// 最后要检查 right 越界的情况
if (right < 0 || nums[right] != target)
return -1;
return right;
}
代码实现
基本数据结构:数组
辅助数据结构:无
算法:二分查找
技巧:无
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @param target int整型
* @return int整型
*/
public int search (int[] nums, int target) {
// 1 入参判断
if (nums.length == 0) {
return -1;
}
// 2 定义左右边界
int left = 0;
int right = nums.length - 1;
// 3 二分查找目标值
while (left <= right) {
int mid = left + (right - left) / 2;
if (target == nums[mid]) {
return mid;
} else if (target > nums[mid]) {
left = mid + 1;
} else if (target < nums[mid]) {
right = mid - 1;
}
}
return -1;
}
}
复杂度分析
- 时间复杂度 O(LogN) :二分查找,只需查找对数阶次即可
- 空间复杂度 O(1) : 没有使用额外空间。
在排序数组中查找元素的第一个和最后一个位置【MID】
依据以上对二分的左右边界分析,来做一道包含重复元素的二分查找
题干
难度升级,找到重复元素的左右边界
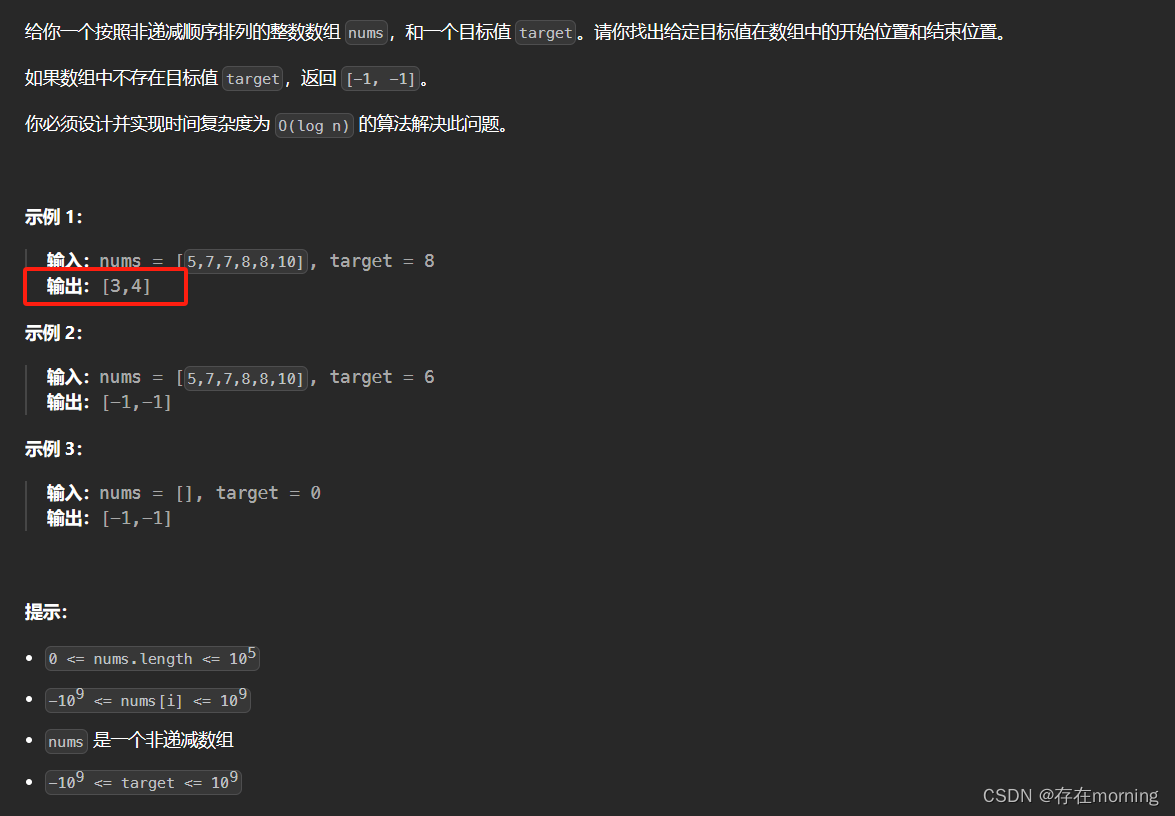
解题思路
以上解题思路相同,需要注意的是:
- 查找左边界时:由于 while 的退出条件是
left = right + 1,且返回的是左边界的坐标,所以当 target 比 nums 中所有元素都大时,会存在以下情况使得索引越界:
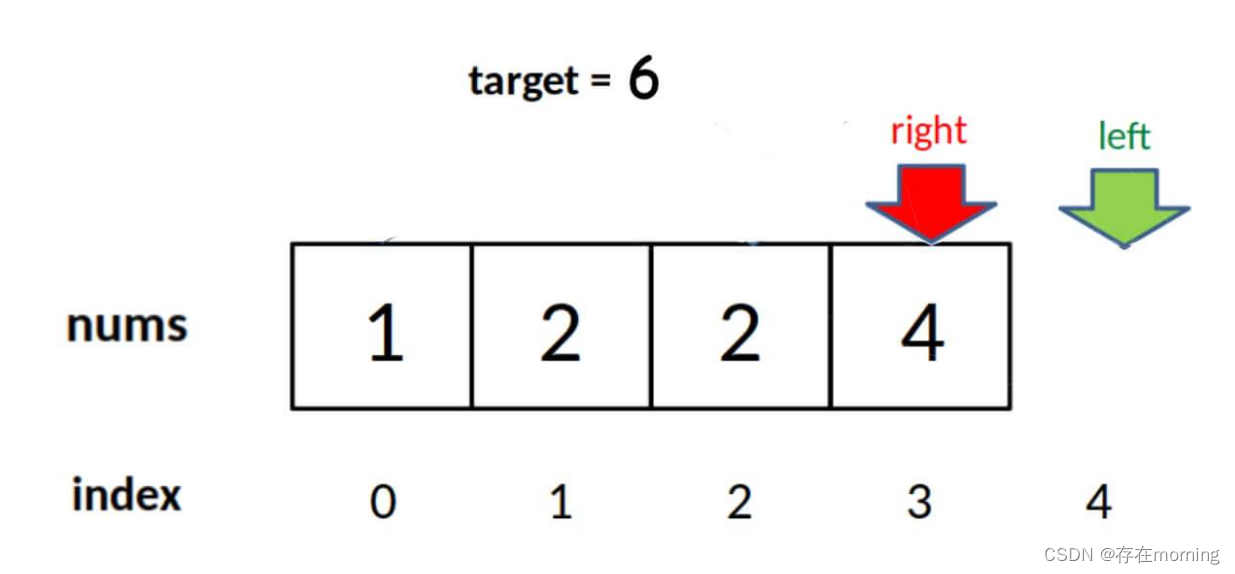
所以要进行一个判断,返回左边界前确认左边界没有超出数组范围
if (left >= nums.length || nums[left] != target)
return -1;
return left;
- 查找右边界的时候也同理
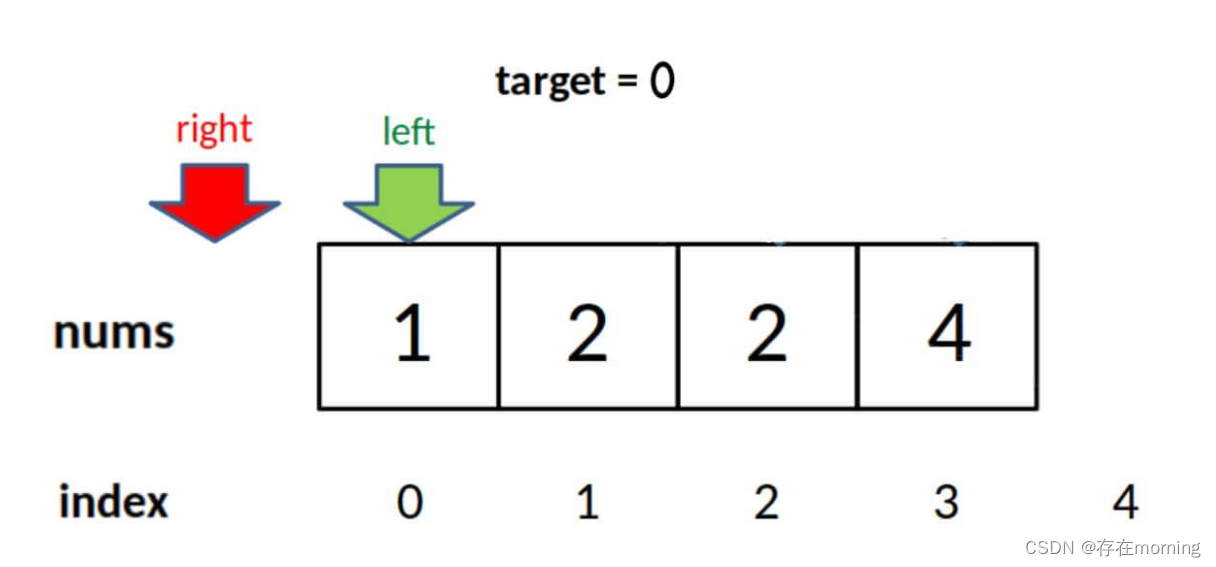
// 这里改为检查 right 越界的情况,见下图
if (right < 0 || nums[right] != target)
return -1;
return right;
代码实现
基本数据结构:数组
辅助数据结构:无
算法:二分查找
技巧:无
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] result = new int[2];
result[0] = leftBound(nums, target);
result[1] = rightBound(nums, target);
return result;
}
private int leftBound(int[] nums, int target) {
// 1 入参判断
if (nums.length == 0) {
return -1;
}
// 2 定义左右边界
int left = 0;
int right = nums.length - 1;
// 3 二分查找目标值
while (left <= right) {
int mid = left + (right - left) / 2;
if (target == nums[mid]) {
// 锁死左边界
right = mid - 1;;
} else if (target > nums[mid]) {
left = mid + 1;
} else if (target < nums[mid]) {
right = mid - 1;
}
}
if (left >= nums.length || nums[left] != target) {
return -1;
}
return left;
}
private int rightBound(int[] nums, int target) {
// 1 入参判断
if (nums.length == 0) {
return -1;
}
// 2 定义左右边界
int left = 0;
int right = nums.length - 1;
// 3 二分查找目标值
while (left <= right) {
int mid = left + (right - left) / 2;
if (target == nums[mid]) {
// 锁死右边界
left = mid + 1;;
} else if (target > nums[mid]) {
left = mid + 1;
} else if (target < nums[mid]) {
right = mid - 1;
}
}
if (right < 0 || nums[right] != target) {
return -1;
}
return right;
}
}
复杂度分析
- 时间复杂度 O(LogN) :二分查找,只需查找对数阶次即可
- 空间复杂度 O(1) : 没有使用额外空间。