玩转快速排序(C语言版)

W...Y的主页 😊

代码仓库分享 💕

🍔前言：

本篇文章，我们来讲解一下神秘的快速排序。对于快速排序我相信大家都已经有所耳闻，但是快速排序是有很多的版本的。我们这次的目的就是快排的所有内容搞懂，废话不多说，让我们开始今天的内容。

🍟目录

快排的介绍

hoare版本

单趟排序

多趟排序

挖坑法

前后指针版本(双指针)

快排的优化

三数取中

小区间优化

快速排序之非递归

快排的介绍

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

基本思想：

选择一个基准元素（pivot）。可以选择数据集中的任意一个元素作为基准，一般情况下选择第一个元素或者最后一个元素作为基准。

将数据集中的其他元素按照与基准元素的大小关系进行分区。将小于基准的元素放在基准的左边，将大于基准的元素放在基准的右边。这个过程称为分区操作。

对分区后的左右两个子集，分别递归地应用相同的方法，继续进行分区操作，直到每个子集只包含一个元素或为空。

最后，将所有子集按照顺序拼接起来，就得到了一个有序的数据集。

快速排序的基本框架：

// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
if(right - left <= 1)
return;
// 按照基准值对array数组的 [left, right)区间中的元素进行划分
int div = partion(array, left, right);
// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
// 递归排[left, div)
QuickSort(array, left, div);
// 递归排[div+1, right)
QuickSort(array, div+1, right);
}

上述为快速排序递归实现的主框架，发现与二叉树前序遍历规则非常像，同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来，后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。

接下来我们来开始进入快速排序！！！

hoare版本

这是最原始的版本，也是第一代创始人hoare发明的版本。我们先来进行快排的单趟交换过程：

单趟排序

这张图片就是hoare版本的全部过程，我们先来分析第一次的交换过程。

单趟过程：首先选取数组最左边的元素标记为key，然后创建两个指针left与right分布到数组的两边。right的指针先走，寻找比key小的元素，找不到就往前走，找到就停止。然后left后走，寻找比key值大的元素，找到后两个值交换即可。

然后我们来看一下单趟的代码：

while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
		{
			--right;
		}
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}
		Swap(&a[left], &a[right]);
	}

代码易错点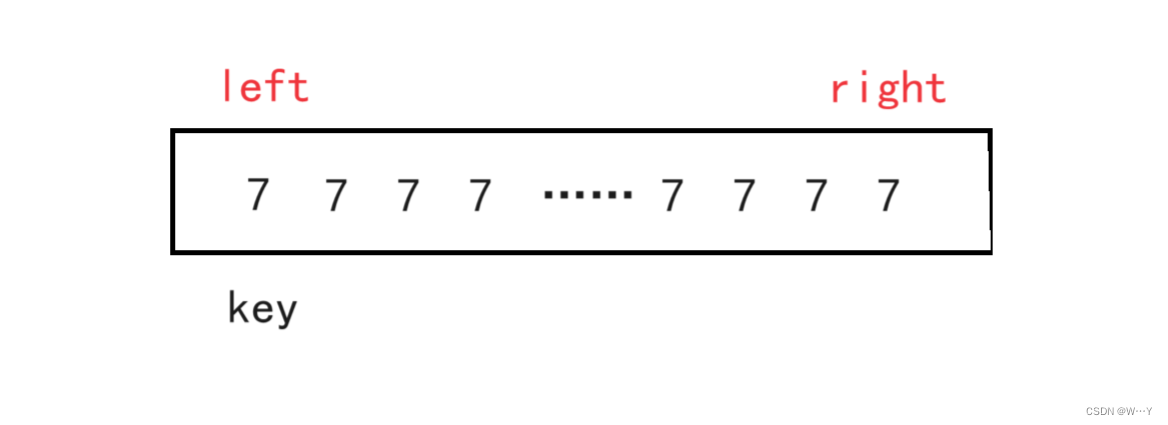： 1. 假设数组为上图数组，right寻找比key小的值，right指针就会一直往前寻找，就会导致数组越界。所以我们必须在while循环条件中加入(left<right)。

2.我们在while循环中可以看到第二个判断条件，是否加等于号。必须要加等于号，否则当left与right指向的元素相等时，交换后的数组继续进行循环就会出现死循环。下图为特殊情况图: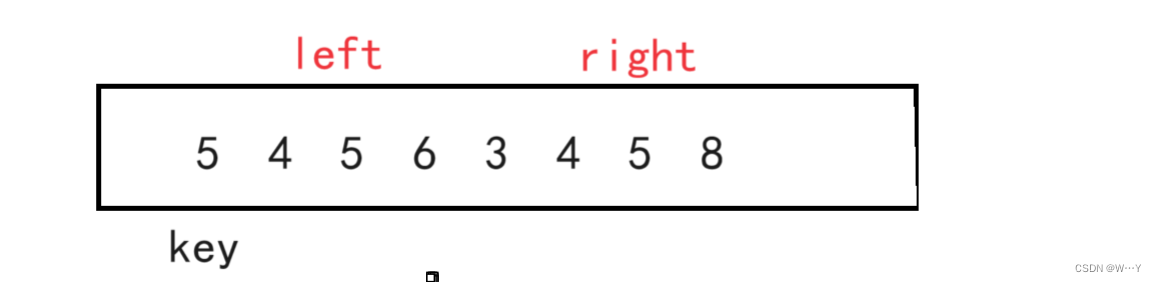

多趟排序

当上面的单趟走完后，我们会发现，keyi左边的全是小于a[keyi]的，右边全是大于a[keyi]的。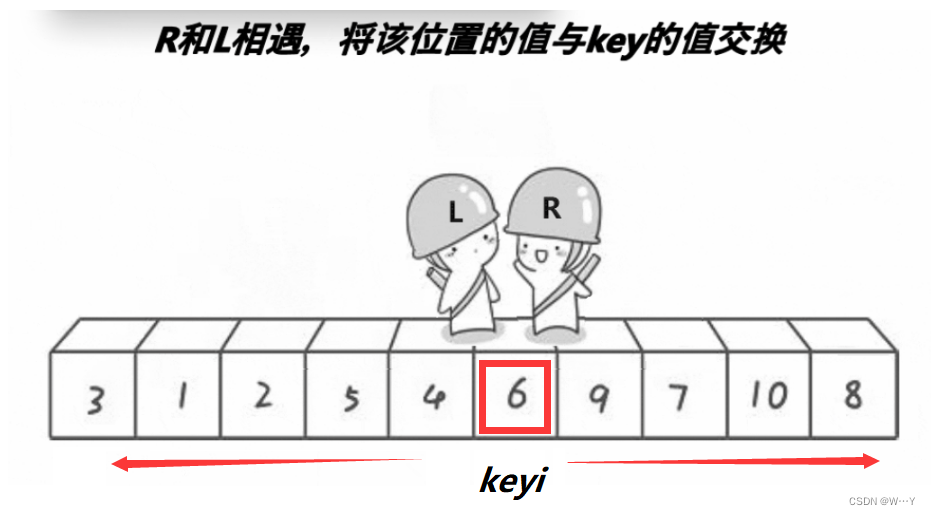

当交换完所有的数后，left指针与right指针就会相遇，我们将相遇的地方与key元素交换即可完成一次排序。现在的数组相对于刚才已经变得有序了一点。我们可以分割重复这个思想，就可以完成整个排序。

分割思路：

类似于二叉树思想，我们可以将其进行风格key左边的都小于key，key右边的都大于key。将数组从key中间一分为二。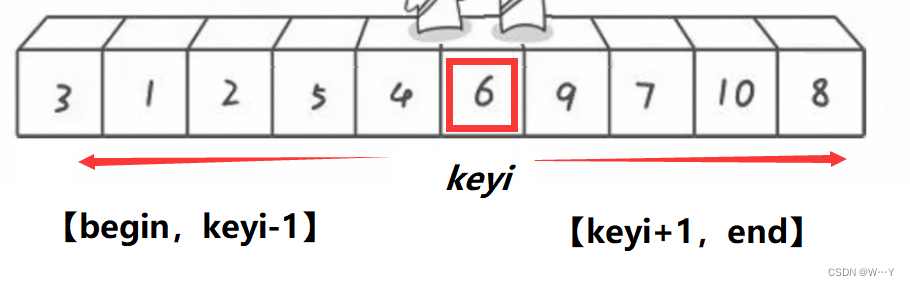

将数组划分为[begin,keyi-1], keyi, [keyi+1,end]，然后与上面单趟排序思想一致，继续进行递归排序。递归结束条件：当begin == end 或者是数组错误(begin>end)时，则为结束条件。

那为什么相遇位置一定比key小呢？怎么确定的？

这就要多亏与right指针先走。

相遇情况：

1.R动L不动，去跟L相遇。相遇位置一定是R的位置，L和R在上一轮交换过，交换以后L的位置的值一定比key小。

2.L动R不动，去跟R相遇。相遇位置一定是L的位置，L的位置比key小。

完整代码如下：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
int PartSort(int* a, int left, int right)
{
	int keyi = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
		{
			--right;
		}
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	return left;
}
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	int keyi = PartSort3(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

挖坑法

对于hoare版本，许多人会觉得不好理解，觉得非常抽像。现在我们来讲一种更加直观的方法，虽然算法思路一样，但是更容易理解。

我们先来看一下思路流程图：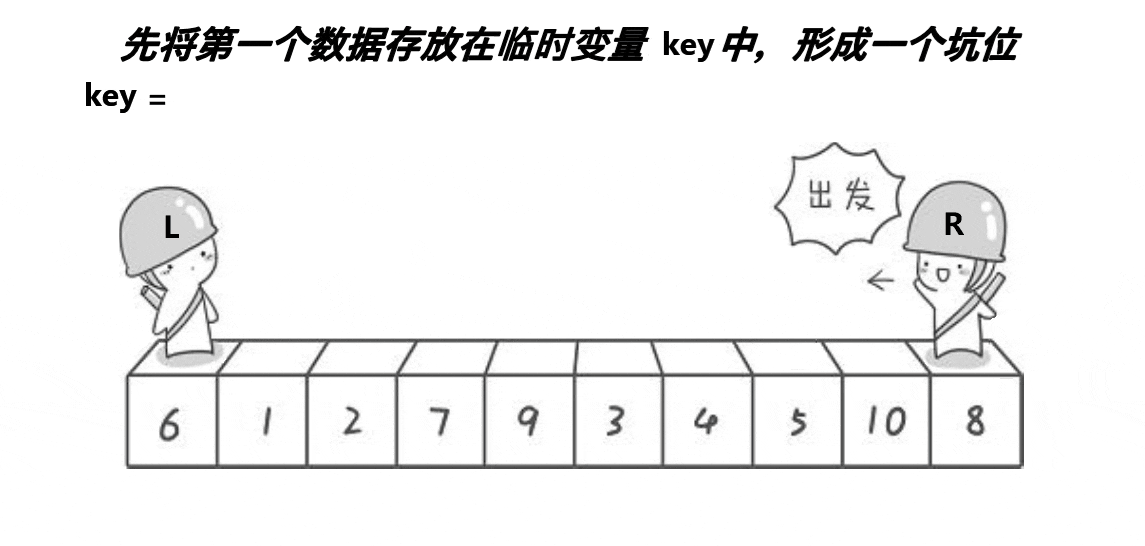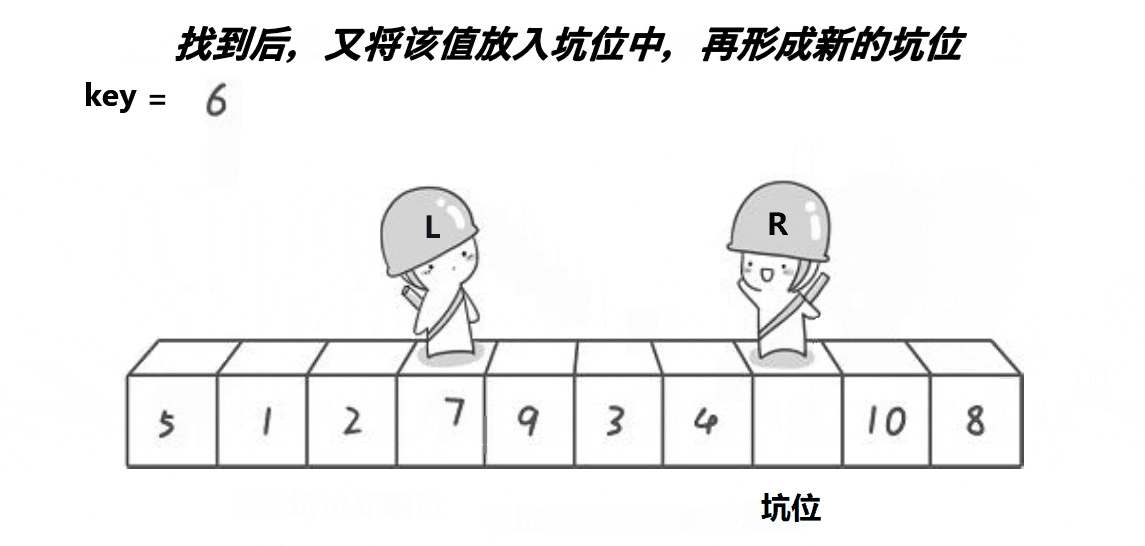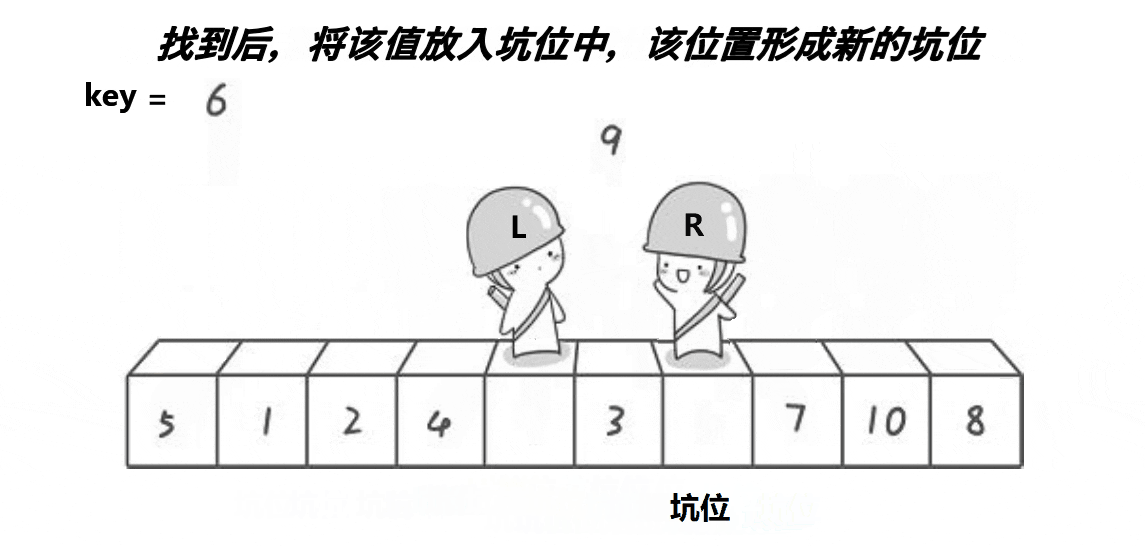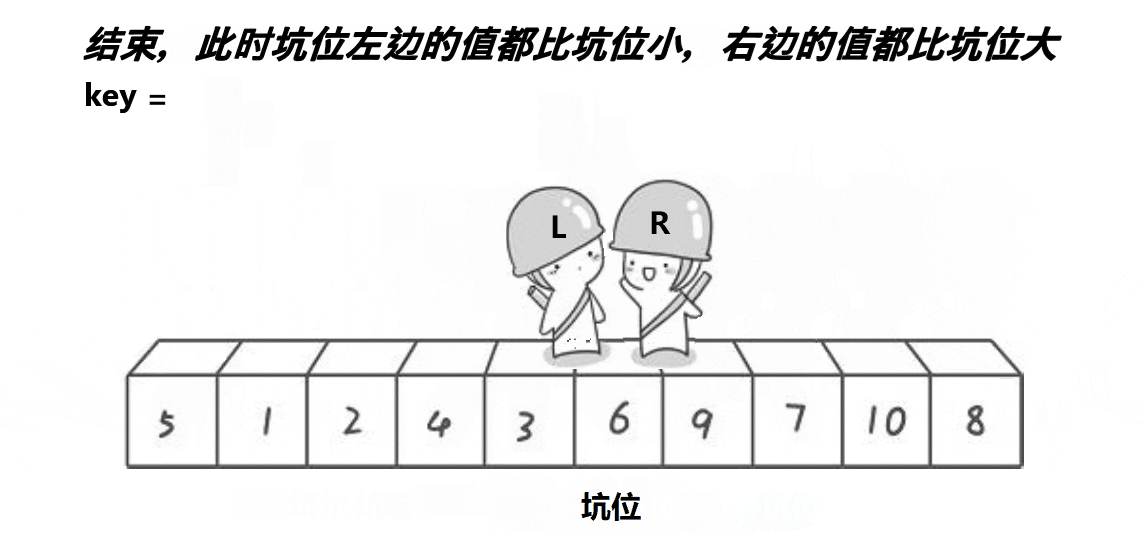

算法思路：

将最左边设置为key并且设置为坑位。什么是坑位，就是将其看成空位。所以我们就要将key对应的元素值进行标记存储防止被覆盖。然后创建两个指针left与right，与key值进行比较。right先走寻找比key小的值，找到后将其填入坑中。然后right指向的数组成为新的坑位。right停止left寻找比key大的元素，找到后将其移动到新坑位，这样依次类推即可。

大致思路与hoare版本相同，唯一不同点就是加入了”坑位“，我们可以看作数组的填空。

在这里我们就不过多赘述了，直接展示源代码：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
int PartSort2(int* a, int left, int right)
{
	int hoop = a[left];
	while (left < right)
	{
		while (left < right && a[right] >= hoop)
		{
			right--;
		}
		a[left] = a[right];
		while (left < right && a[left] <= hoop)
		{
			left++;
		}
		a[right] = a[left];
	}
	a[left] = hoop;
	return left;
}
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	int keyi = PartSort3(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

这里我们还是使用了递归的思想进行操作。

前后指针版本(双指针)

前后指针的思路与前两个有很大的区别，也是目前最流行的写法。我们还是从图中了解一下其中原理。

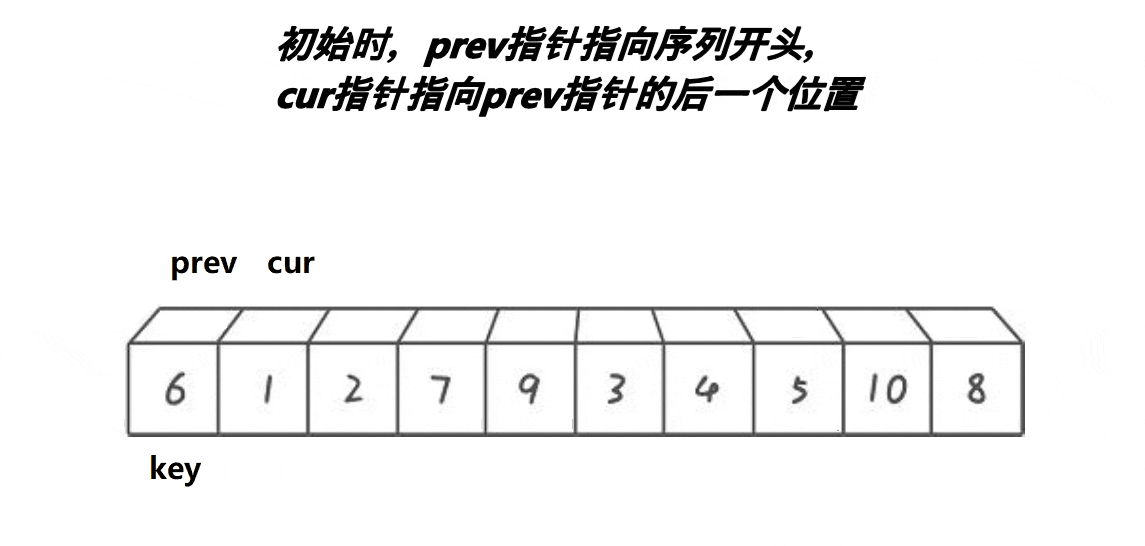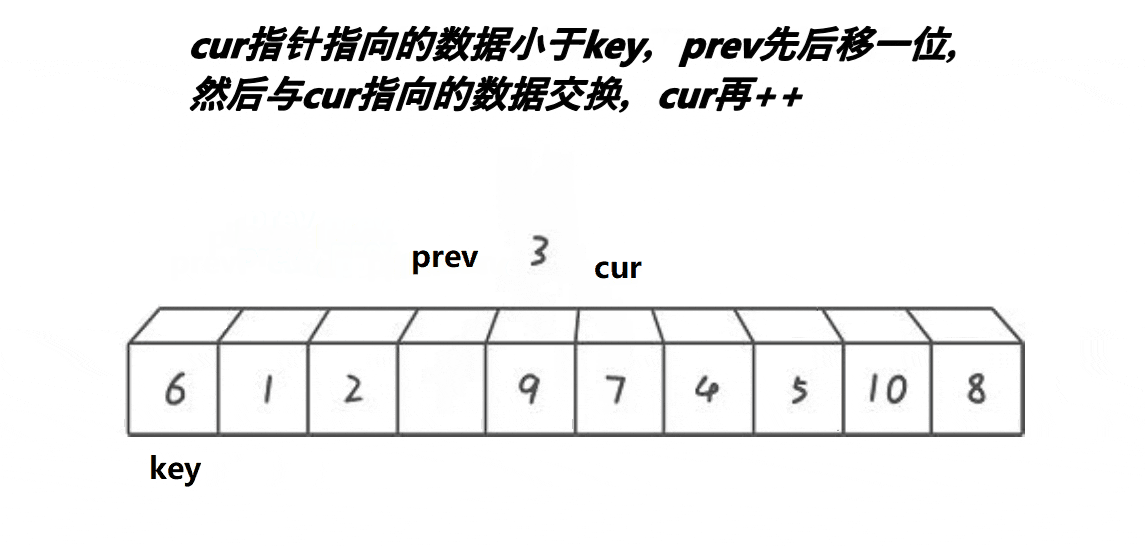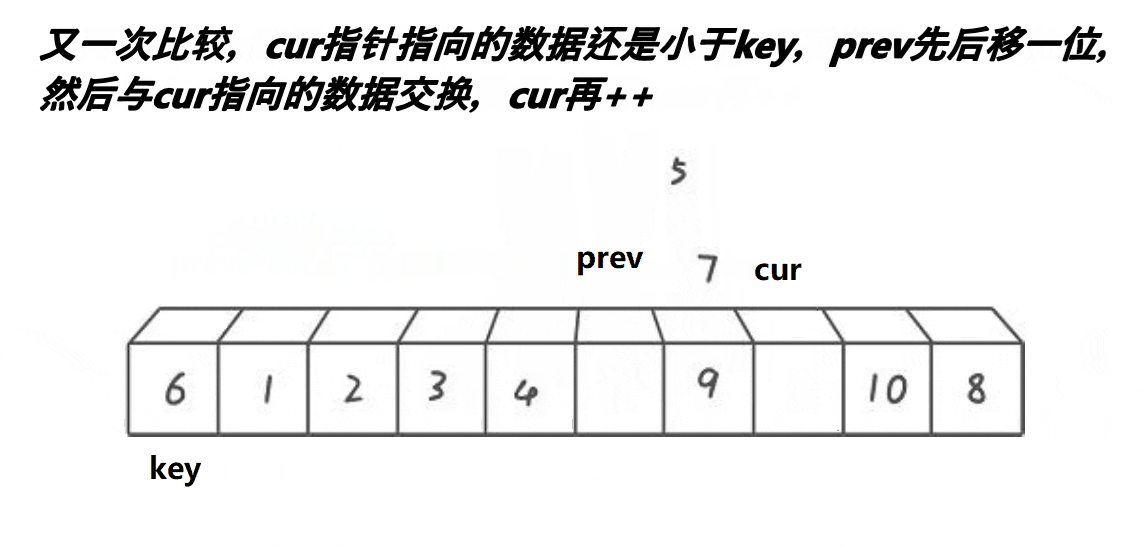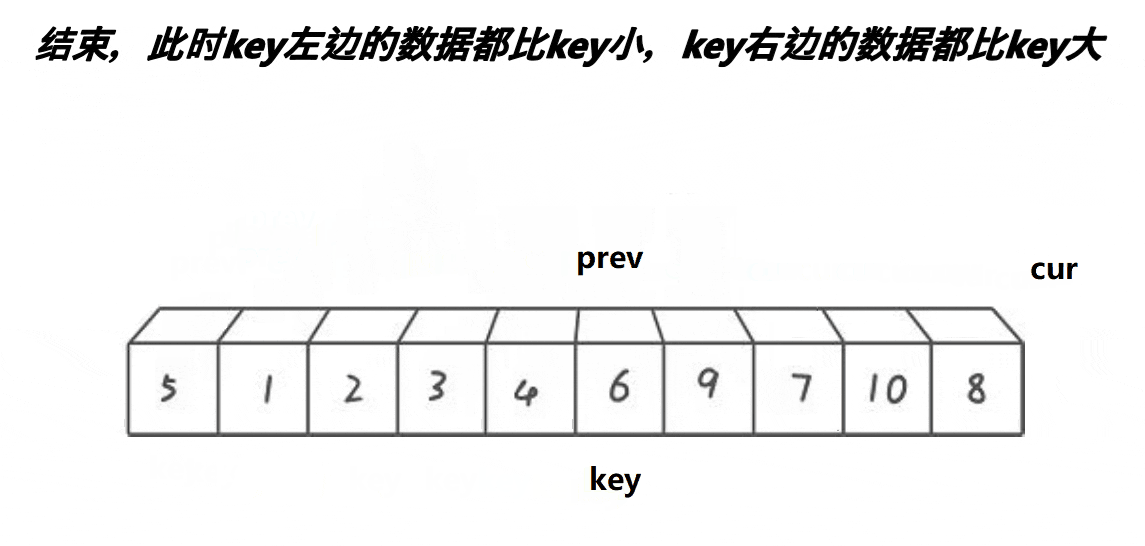
算法思路：

创建两个指针变量，一个prev指向最开始节点，cur指针指向prev的后方，也就是cur = prev + 1。cur去寻找比key大的值，如果cur指向比key小，prev先加1然后进行交换(在前面如果没遇到比key大的值，就相当于自己给自己赋值)。当遇到比key大的值时，prev不动，cur++。直到cur>=数组长度end即可停止。当循环结束，我们将prev指向的位置与key交换，这样单趟思路就搞定了。

多趟思路就是进行拆分递归，下来就是代码展示：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
int PartSort3(int* a, int left, int right)
{
	int keyi = left;
	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	return prev;
}
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	int keyi = PartSort3(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

注意：在遍历时，判断++prev != cur可以去掉，这样做是防止自己给自己赋值，优化程序。

快排的优化

三数取中

快排的速度非常快，一般情况下为O(nlogn)，但是在特殊情况下速度就会特别慢，达到了O(n^2).那是什么情况下会出现这种场景呢？
key是取决于速度快慢的关键，当key值取到的值为数组元素的中间值时就非常理想。

但是如果这个数组是比较有序的，每次取到的key值都是最大值或最小值，那么指针在寻找需要的元素时基本都会直接遍历整个数组。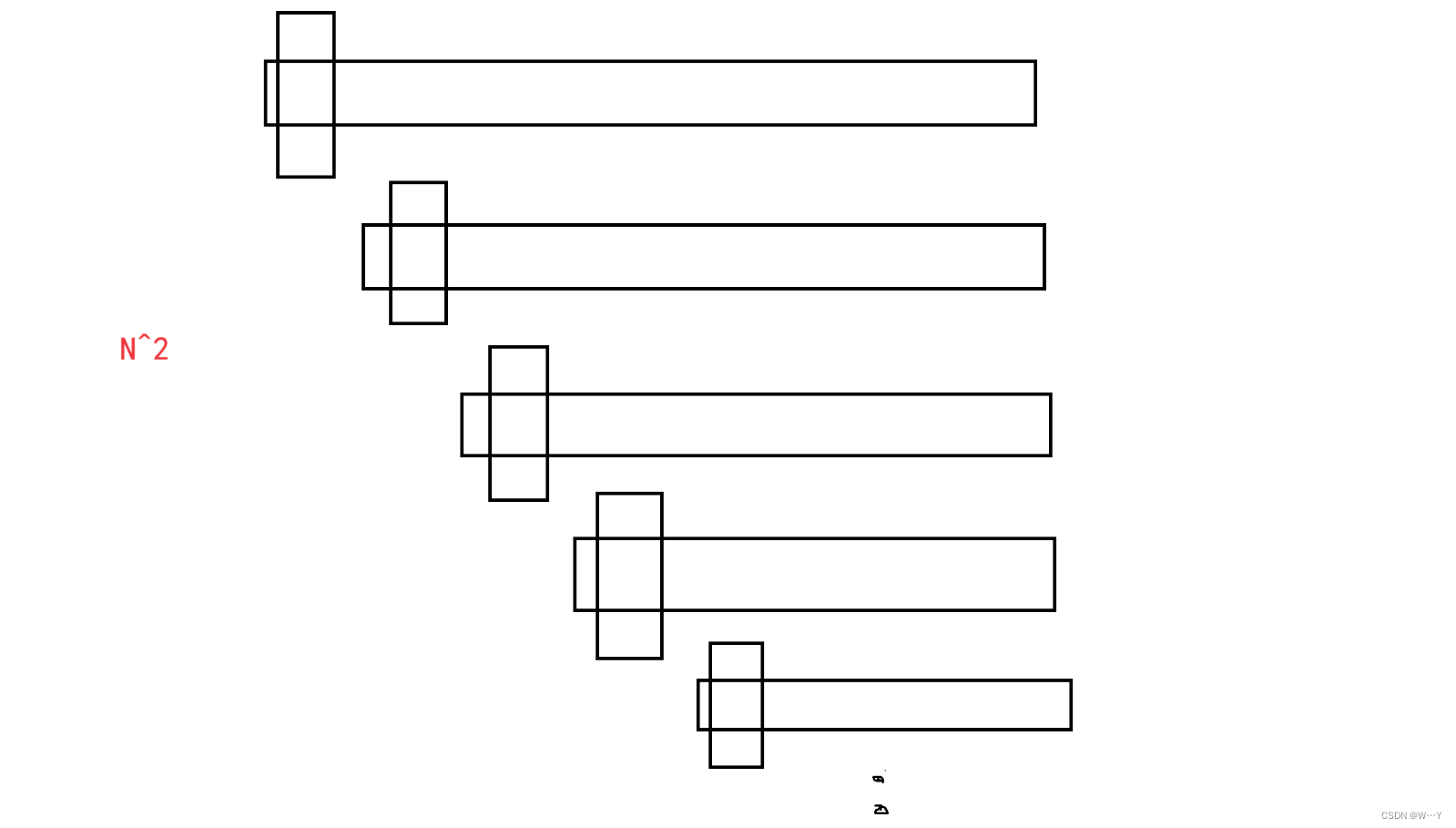所以我们就需要进行”三数取中“，我们知道数组的头尾，就可以算出数组的中间值，我们将这三个位置的数组进行比较，取最中间的值作为key即可。

这样做就可以优化快排最坏的情况，让时间复杂的基本维持到O(nlogn)。

代码展示：

int GetMidi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
			return right;
	}
	else // a[left] > a[mid]
	{
		if (a[left] < a[right])
		{
			return left;
		}
		else if (a[right] > a[mid])
		{
			return right;
		}
		else
			return mid;
	}
}

小区间优化

对于大量的数，我们可以使用快速排序，但是一些小区间的数使用快排反而没有插入排序……效率高，所以我们进行小区间优化。如果数组大小小于10个，我们就使用插入排序即可，如果大于10个数就可以使用快排进行。

void QuickSort1(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	if ((end - begin + 1) > 10)
	{
		int keyi = PartSort3(a, begin, end);
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
	else
	{
		InsertSort(a + begin, end - begin + 1);
	}
}

插入排序的源代码在这寻找：插入排序之希尔排序——【数据结构】-CSDN博客

使用插入排序区间不一定是从头开始，所以在传参时要加begin。

快速排序之非递归

因为函数递归实在栈上开辟空间的，而栈上的空间只有4G左右，如果递归层数太深就会导致栈溢出。而非递归就是在堆上开辟空间，堆的空间非常大，我们有足够的空间去开辟，所以我们就使用非递归来完成。

算法思路：

我们利用栈先进后出的优势，存储其前后区间即可。假设数组区间为0~9，我们先存储右边再存储左边(因为取值时就可以先取左边再取出右边)，然后进行函数调用排序将区间划分为[left , keyi - 1] keyi [ keyi + 1 , right ] ,再将区间的值进行右左入栈，然后再取两个值作为区间进行函数调用以此类推，直到栈为空为止。

我们将函数的递归转换成用栈来取区间。

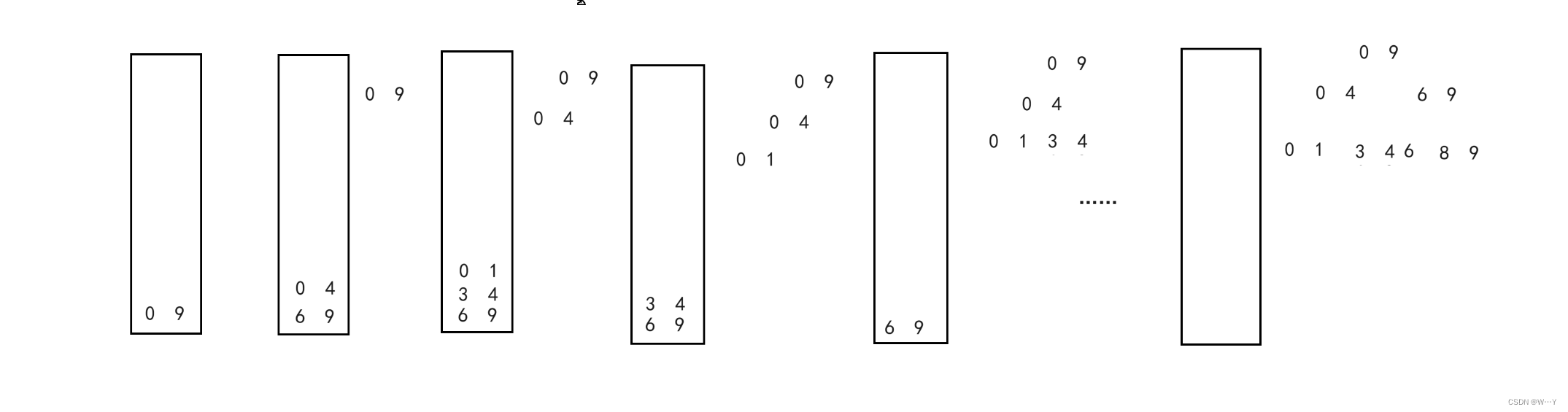
注意：一定要先存储右边，再存储左边

代码展示：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;

void STInit(ST* ps);
void STDestroy(ST* ps);
void STPush(ST* ps, STDataType x);
void STPop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);
STDataType STTop(ST* ps);
#define _CRT_SECURE_NO_WARNINGS 1
#include"Stack.h"
void STInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;
}
void STDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}
void STPush(ST* ps, STDataType x)
{
	assert(ps);
	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newCapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
}
void STPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);

	--ps->top;
}
int STSize(ST* ps)
{
	assert(ps);

	return ps->top;
}
bool STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}
STDataType STTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);

	return ps->a[ps->top - 1];
}
void QuickSortNonR(int* a, int begin, int end)
{
	ST st;
	STInit(&st);
	STPush(&st, end);
	STPush(&st, begin);
	while (!STEmpty(&st))
	{
		int left = STTop(&st);
		STPop(&st);
		int right = STTop(&st);
		STPop(&st);

		int keyi = PartSort3(a, left, right);
		if (keyi + 1 < right)
		{
			STPush(&st, right);
			STPush(&st, keyi + 1);
		}
		if (left < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, left);
		}
	}

	STDestroy(&st);
}

以上是本次快速排序全部内容，对大家有帮助的麻烦三连支持一下!!!