图谱滤波（Graph Spectral Processing）-1

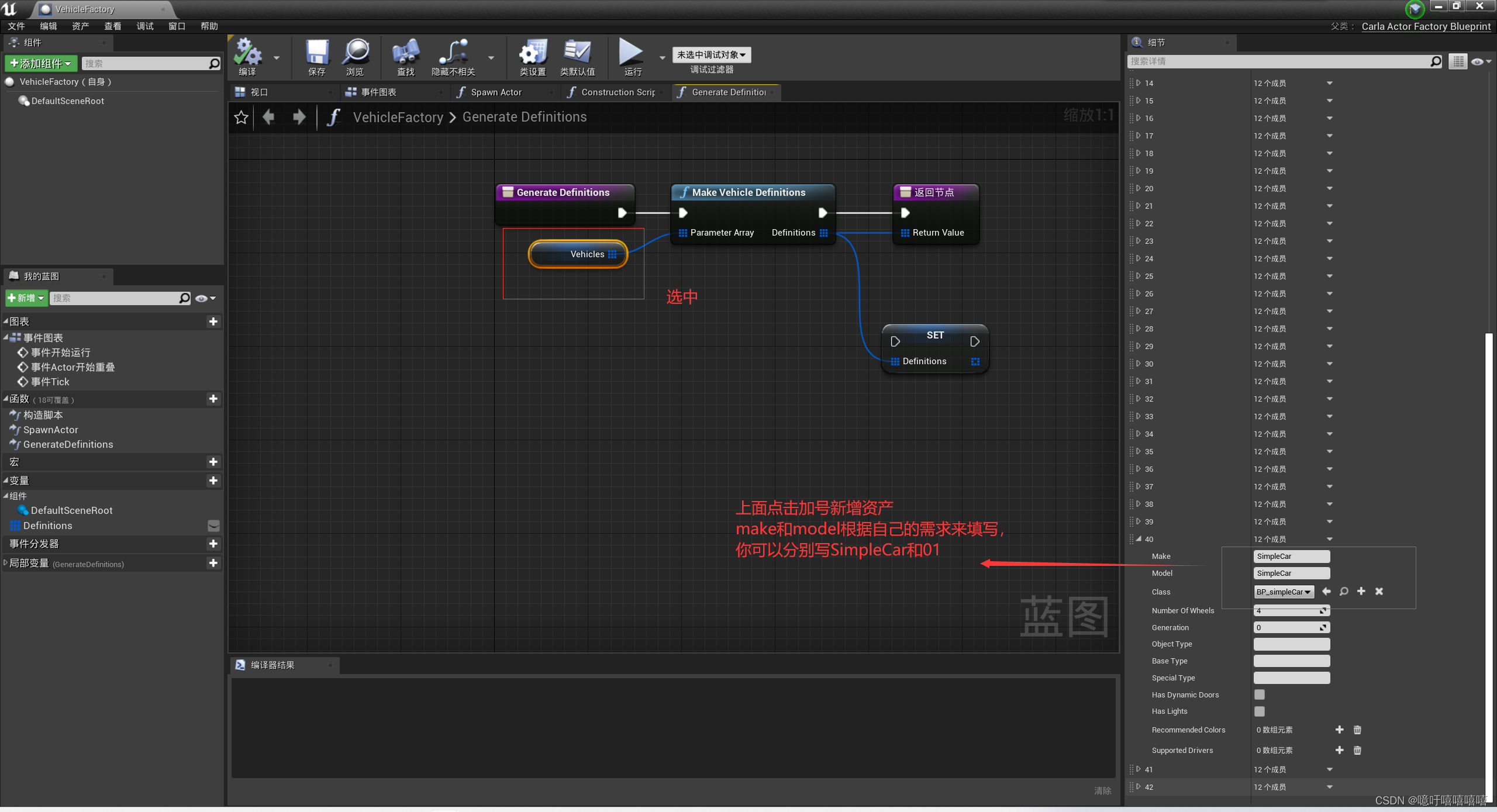
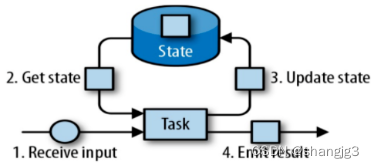
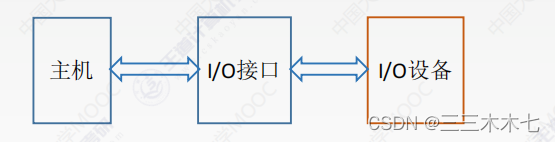
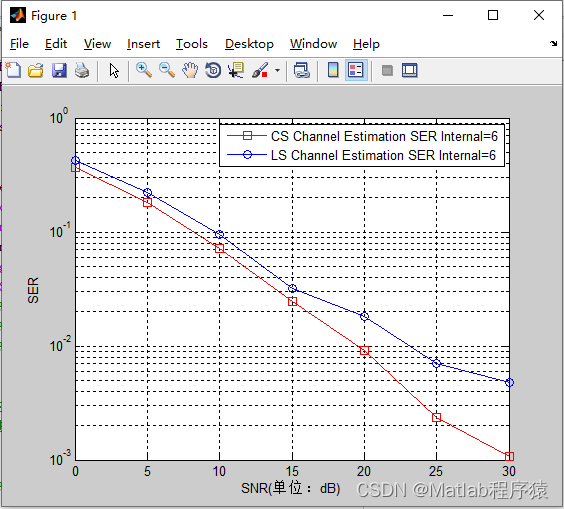
时域和空域信号的滤波是图像处理的基本技术之一，迄今已得到广泛的研究。Graph Spectral Processing(GSP)可以处理不规则结构的信号，这些信号在数学上用图形表示。利用谱图理论研究了图信号滤波的理论和方法。在图像处理中，图是表示像素形成的结构的强有力工具，如边和纹理。

图信号的滤波不仅是对标准时域和空域信号滤波的扩展，而且具有自身的性质特点。例如，GSP可以将传统的基于像素的图像滤波方法表示为图谱域滤波器。此外，在信号和图像处理中被广泛研究的小波和滤波器组的理论和设计方法也被用于图信号的处理。

1、时域信号滤波

在离散时间线性时不变(Linear Time-Invariant LTI )系统的滤波中，假设一维离散时间信号 $x_{n}$ 是通过对其连续时间对应信号 $x(t)$ 进行采样得到的，采样周期 $T$ 固定，即 $x_{n}=x(n T)$ 。在水平和垂直两个方向上进行采样，同样可以得到二维图像信号。所以，空间采样周期通常对应一个光学传感器阵列之间的间距。假设先验给定一个滤波器 $h_{n}$ 的脉冲响应，LTI系统中的离散时间滤波信号 $y_{n}$ 由 $x_{n}$ 和 $h_{n}$ 通过卷积计算如下：

$y_{n}=h_{n} * x_{n}:=\sum_{k=-\infty}^{\infty} h_{n-k} x_{k}=\sum_{k=-\infty}^{\infty} x_{n-k} h_{k}$

众所周知，时域中的卷积运算在频率(即频率)中有一个等价的表达式如下：

$\hat{y}(\omega)=\hat{h}(\omega) \hat{x}(\omega)$

即：

$\hat{x}(\omega):=\sum_{n=-\infty}^{\infty} x_{n} e^{-j \omega n}$

其中， $\hat{x}(\omega)$ 为 $x_{n}$ 的离散时间傅里叶变换( DTFT )，时域卷积与频域乘法可视为等价运算。固定滤波器具有相应的固定频率响应，因此可以从频率响应直观地了解滤波器特性。相比之下，信号相关滤波器的频率响应在一般情况下并不总是清楚的，但这种缺点可以用图谱域视角得到部分解决。

2、图形信号滤波

首先考虑线性图滤波器，深度学习中使用的滤波器为非线性图形滤波器。在LTI系统中，滤波后的信号表示为：

$\mathbf{y}=\mathbf{H x}$

其元素 $x_{n}$ 的表示与时域滤波方程中相同，即：

$y_{n}:=\sum_{k=0}^{N-1}[\mathbf{H}]_{n, k} x_{k}$

其中， $[\cdot]_{n, k}$ 是矩阵中的n，k元素，与离散时间信号类似，图信号滤波可以定义在顶点域(Vertex Domain)和图频域(Graph Spectral Domain)两种方式。

2.1 Vertex Domain

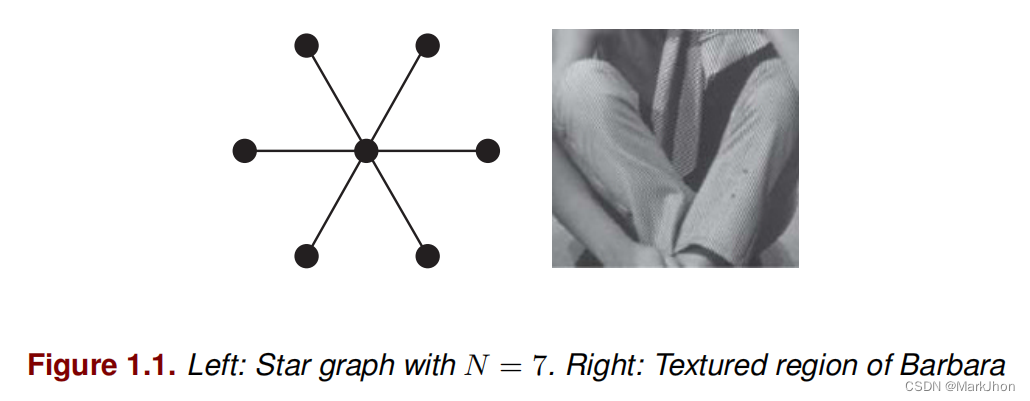
顶点域滤波是时域滤波的一种模拟，但是图信号处理(GSP)系统不是移位不变的。这意味着节点索引一般不具有任何物理意义。因此基于节点指标的图信号移位，类似于离散时间信号的移位不具有实用性。此外底层图会表现出高度不规则的连通性，即每个节点的度会有很大的变化。例如，图1.1所示的星图有一个中心节点和N-1个周围节点。显然，N-1条边与中心节点相连，即中心节点有度N-1，而周围所有节点都有度1。在图像处理的角度，这样的不规则性来源于边缘和纹理区域。图1.1右侧提供了一个示例。如同我们构造一个基于像素强度的图，即像素是节点，它们之间通过权值w较高的边相连。

顶点域过滤可定义如下，设 $\mathcal{N}_{n, p}$ 为第 $n$ 个节点的一个集合的第 $p$ 个邻域节点，显然 $\left|\mathcal{N}_{n, p}\right|$ 随 $n$ 而变化。图谱滤波的顶点域滤波，通常可以定义为邻域样本的局部线性组合：

$y_{n}:=\sum_{k \in \mathcal{N}_{n, p}}[\mathbf{H}]_{n, k} x_{k}$

由于 $\mathcal{N}_{n, p}$ 随 $n$ 的变化， $[{H}]_{n, k}$ 所有 $n$ 的 $k$ 应该适当地确定，方程的矩阵形式可以表示为:

$\mathbf{y}=\left(\operatorname{diag}\left([\mathbf{H}]_{0,0}, \ldots,[\mathbf{H}]_{N-1, N-1}\right)+h(\mathbf{W})\right) \mathbf{x}$

其中 $h(\mathbf{W})$ 是一个包含滤波器系数 $h[n,k](n=k)$ 作为邻接矩阵 $\mathbf{W}$ 的函数的矩阵，其中 $[h(\mathbf{W})]_{n, k}=0$ ，如果 $k \notin \mathcal{N}_{n, p}$ 。方程[1.9]和[1.10]中的顶点域滤波一般需要确定 $\sum_{n}\left|\mathcal{N}_{n, p}\right|$ 滤波器系数；此外它有时需要增加计算复杂度。通常 $[\mathbf{H}]_{n, k}$ 可以参数化为以下形式：

$\mathbf{y}=\left(\sum_{p=0}^{P-1} h_{p} \mathbf{W}_{p}\right) \mathbf{x}$

其中 $h_{p}$ 是一个实值， $\mathbf{W}_{p} \in \mathbb{R}^{N \times N}$ 是一个掩蔽邻接矩阵，只包含w的跳包邻域元素，表示为

$\left[\mathbf{W}_{p}\right]_{n, k}= \begin{cases}{[\mathbf{W}]_{n, k}} & \text { if } k \in \mathcal{N}_{n, p} \\ 0 & \text { otherwise }\end{cases}$

方程中所要求的参数数为P，明显小于第一个方程中所要求的参数数量。我们可以发现方程的时域滤波与参数化顶点域滤波有相似之处。事实上，如果基础图是一个循环图，两个方程存在一致性。但是，在一般情况下它们不一致：由于图的不规则性质，很容易证实滤波系数矩阵的和不是常数，而在时域滤波中确是一个常数。因此，应仔细确定滤波系数矩阵的参数。

2.2 Graph Spectral Domain

上文引入的顶点域滤波能够直观地并行于时域滤波，但是从频率的角度看仍然存在不足。时域滤波和频域滤波与DTFT(Discrete-time Fourier Transform)完全相同。但一般来说，这种简单的关系在实际使用中并不适用。顶点域滤波方程的简单实现并不反映在图频域上有对角线响应变化。即滤波器系数矩阵H并不总是可以被GFT矩阵U对角化，即UHU一般不是对角化的。因此当在顶点域内进行滤波时，H的图频率响应并不存在清晰的对应关系。这是离散时间信号和图信号的滤波之间的明显的区别。

定义在图频域的图信号滤波是傅里叶域滤波的模拟，其中图信号滤波的谱域定义具有许多理想的特性：对角图频率响应；快速计算；像素相关图像滤波的可解释性为图谱滤波。根据以上对应， $h_{n}$ 和 $x_{n}$ 在时域上的卷积是 $\hat{h}(\omega)$ 和 $\hat{x}(\omega)$ 在傅里叶域上的乘积，图频域的滤波利用这种模拟来定义广义卷积(Shumanetal.2016b)：

$\hat{y}_{i}:=\hat{h}\left(\lambda_{i}\right) \hat{x}_{i}$

其中 $\hat{x}_{i}=\left\langle\mathbf{u}_{i}, \mathbf{x}\right\rangle$ 是x的第i个GFT系数，图算子方程的特征分解给出了GFT基 $u_{i}$ ,此外， $\hat{h}(\lambda_{i})$ 是图滤波器的图频率响应。通过将ˆy转换为 $y_{n}=\sum_{i=0}^{N-1} \hat{y}_{i}\left[\mathbf{u}_{i}\right]_{n}$ 可得到 $y[n]$ ，其中 $\left[\mathbf{u}_{i}\right]_{n}$ 是 $u_{i}$ 的第 $n$ 个元素。这同样是用矩阵的形式写成的:

$\begin{aligned} \mathbf{y} &=\mathbf{U}\left[\begin{array}{lll} \hat{h}\left(\lambda_{0}\right) & & \\ & \ddots & \\ & & \hat{h}\left(\lambda_{N-1}\right) \end{array}\right] \mathbf{U}^{\top} \mathbf{x} \\ &=\left(\sum_{i=0}^{N-1} \hat{h}\left(\lambda_{i}\right) \mathbf{P}_{\lambda_{i}}\right) \mathbf{x} \end{aligned}$

其中：

$\mathbf{P}_{\lambda}:=\sum_{k \in \sigma(\lambda)} \mathbf{u}_{k} \mathbf{u}_{k}^{\top}$

是一个投影矩阵，其中 $\sigma(\lambda)$ 是重复特征值的一组指标，即一组指标，如 $\mathbf{L} \mathbf{u}_{k}=\lambda \mathbf{u}_{k} \text {. }$ 。

假设所有的特征值都是不同的,在给定的GFT基 $U$ 下，通过在 $\hat{h}(\lambda_{i})$ 中指定N个图的频率响应来实现图频域滤波。由于这是一个对角矩阵，如公式所示，其顶点域滤波观察到的频率特性变得相当清晰。请注意，方程的简单实现需要特定的 $\lambda_{i}$ 值，即图的频率值。因此，在滤波之前必须给出图算子的特征值。相反，在这种情况下，我们可以参数化连续谱响应 $\hat{h}(\lambda)$ ， $\lambda \in\left[\lambda_{\min }, \lambda_{\max }\right]$ 。这种与图无关的设计过程已经在许多谱图滤波器中被广泛地应用，因此特征值在不同的谱图滤波器中经常有显著的变化。对于经典的傅里叶域滤波，只要考虑频率范围 $\omega \in[-\pi, \pi]$ （或任意的2π区间）就足够了。然而，图的频率根据底层图和/或所选的图操作符而变化。例如，对称归一化图的拉普拉斯函数在[0,2]，wh内有特征值

$\lambda_{N-1} \leq \max \left\{d_{u}+d_{v} \mid(u, v) \in \mathcal{E}\right\}$

其中 $d_{u}$ 是顶点 $u$ 的度。在文献中也发现了其他一些方面的改进。虽然上面提到的图拉普拉斯函数有一个最大特征值的界，但这些界并不适用于邻接矩阵。考虑到这一点，在设计图滤波器时，必须适当地注意图的频率范围。如前所述，图频域滤波是傅里叶域滤波的一种模拟方法。然而，这并不意味着我们总是得到一个类似于顶点域的表达式。因此，我们需要计算输入信号的GFT，这就提出了如下所述的计算问题。对于GFT，特征向量矩阵U必须由图算子计算出来。对于一个密集的矩阵2，特征分解需要O(N3)的复杂度。这个计算往往变得越来越复杂，特别是对于大数据应用程序，包括图像处理。通常，图形光谱图像处理矢量化图像像素。假设我们有一个大小为W×H像素的灰度图像。它的向量化版本是 $\mathbf{x} \in \mathbb{R}^{W H}$ ，它对应的图算子是 $\mathbb{R}^{W H \times W H}$ 。例如，4K超高清分辨率对应于W=3840和H=2160，这导致了WH>8×10^6：这太大了，无法进行特征分解，即使是最近的高规格计算机也是如此。