目录
1. 决策变量的`Start`属性直接设置变量的初始值
1.1 Start:MIP变量的起始值(初值)double类型,可更改
1.2 StartNodeLimit:限制了在完善一组输入部分变量的初始解时,MIP所探索的分支定界的节点的数量 int类型,可更改
1.3 NumStart:在MIP模型中的初始解的数量,即有几组初始解。(初始化为未定义)int类型,可更改
1.4 StartNumber:当传入多个初始解时 int类型,可更改
2. 设置决策变量的Hint属性,为求解器提供提示
2.1 VarHintVal:用户提示值,即一个变量在MIP模型的高质量解决方案中可能具有的特定值 double类型,可更改
2.2 VarHintPri:用户对于用户提示值的信心水平,该值越大表明用户把握越大 int类型,可更改
3. 使用求解器的callback方法
对于min问题,可行解是提供的UB,要么是通过分支定界探测节点(具体的说是探测松弛节点再加割)找到,要么是通过启发式算法找到。
前者表现在gurobi求解日志里是第一列的*,后者表现在gurobi求解日志里是H。
gurobi内部也嵌套了30多种启发式算法,是普适性的算法,不一定对我们的问题适用。当我们看到gurobi很久都找不到一个可行解(incumbent那一列为空),如下:
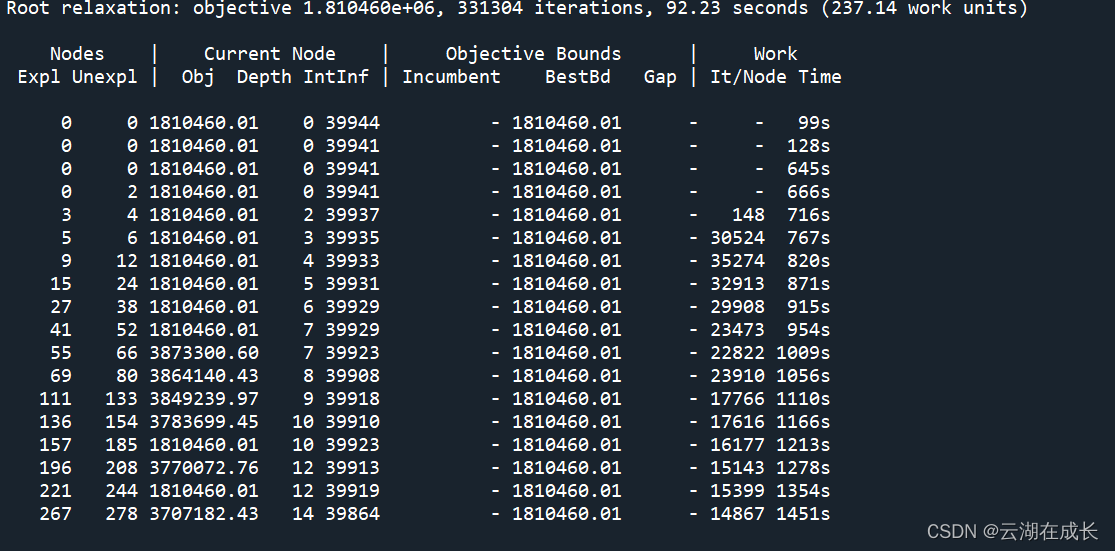
我们可以要么改写模型,写一个更紧一点的模型,本质是探测节点找到可行解。但也可以通过启发式算法传入可行解。
传入的方法有3种:
1. 决策变量的`Start`属性直接设置变量的初始值
这个方法其实简单,效果也不错,以我现在的水平用得比较多。
Start属性可以输入一个或多个可行解,Gurobi会自己将可行解中未定义的变量补全,用户也可以Push求解器努力补全更好的,Gurobi最终会使用最好的可行解进行迭代搜索。
与Start相关的属性有:`Start,StartNodeLimit,StartNumber,NumStart`。
1.1 Start:MIP变量的起始值(初值)double类型,可更改
# 将变量x_1_12的初值设置为0
x[0,12].start = 1.0
# 循环为x_ij赋值完整的一组初始解,data为存放初始解的矩阵
for i in range(len(data)):
for j in range(len(data[i])):
x[i,j].start = data[i][j]1.2 StartNodeLimit:限制了在完善一组输入部分变量的初始解时,MIP所探索的分支定界的节点的数量 int类型,可更改
StartNodeLimit参数的默认值是-1,其使用SubMIPNodes参数的值(即搜索500个分支定界树的节点后停止)。
值为-2表示只检查完整的MIP的Start输入下的可行性,并忽略部分MIP的决策变量的Start。
值为-3将完全关闭MIP的Start通道。
非负的参数值表示探索节点限制个数,比如设置m.setParam(GRB.Param.StartNodeLimit, 10000.0), 表示探索的节点个数上限为10000个。
# 将搜索节点个数设置为10000个点
m.setParam(GRB.Param.StartNodeLimit, 10000.0)1.3 NumStart:在MIP模型中的初始解的数量,即有几组初始解。(初始化为未定义)int类型,可更改
1.4 StartNumber:当传入多个初始解时 int类型,可更改
# 为模型m2设置要输入的初始解个数为2个
m2.NumStart = 2
# 将该可行解设置为第一个输入的可行解
m2.Params.StartNumber = 0
# 将该可行解设置为第二个输入的可行解
m2.Params.StartNumber = 1
# 完整版
# 读取原始模型m
m2 = read("CVRP1.mps")
# 设置NumStart=2,表示可以接受两个可行解作为初值
m2.NumStart = 2
# 提取解池中第5个解
m.setParam(GRB.Param.SolutionNumber, 4)
s5 = m.Xn
# 将该可行解设置为第一个输入的初值
m2.Params.StartNumber = 0
index = 0
for v in m2.getVars():
v.Start = s5[index]
index += 1
# 提取解池中第6个解
m.setParam(GRB.Param.SolutionNumber, 5)
m2.Params.StartNumber = 1
s6 = m.Xn
index = 0
for v in m2.getVars():
v.Start = s6[index]
index += 1
# 输入好初值后更新模型并求解
m2.update()
m2.optimize()
2. 设置决策变量的Hint属性,为求解器提供提示
有的时候我们也找不到可行解,求解器就更加为难了。但是我们通过已有的一些尝试发现某些变量非常有可能的取值情况,此时就可以通过Hint属性来向求解器提示某某变量可能取某个值。注意,如果我们已知一些变量的取值,或者已知一个可行解,我们应该使用Start属性来给求解器提供初值,因为Hint会从全局影响整个迭代搜索的过程。
-
Hint属性是用户提示Gurobi某个变量可能在最优解中的取值,并且用户可以自己设置对这个想法的信心。
-
但是与Start属性不同的是,
Hint会在整个迭代过程中影响着Gurobi的迭代搜索,因此如果很确信的话,还是拿Start来构建初值比较好。start建构是100%建构,Hint是程度。
2.1 VarHintVal:用户提示值,即一个变量在MIP模型的高质量解决方案中可能具有的特定值 double类型,可更改
2.2 VarHintPri:用户对于用户提示值的信心水平,该值越大表明用户把握越大 int类型,可更改
#设置x[0,18]可能=1,信心为50
x[0,18].VarHintVal = 1.0
x[0,18].VarHintPri = 50
#设置x[0,13]可能=1,信心为25
x[0, 13].VarHintVal = 1.0
x[0, 13].VarHintPri = 25
#设置x[0,6]可能=1,信心为25
x[0, 6].VarHintVal = 1.0
x[0, 6].VarHintPri = 253. 使用求解器的callback方法
Callback(回调)是求解器的一种高级功能,可以用于监视求解进程、获取求解进程信息,甚至干预求解算法等。Callback不同于上文介绍的设置变量的Start属性和Hint属性的方法。
Callback是一个比较神奇的技术,它需要在求解过程中靠我们插手“半自动的”进行迭代搜索,我们设置的callback会在迭代中影响着Gurobi的求解,往往和一些cut算法结合。
gurobi中callback函数的使用整理_gurobi callback-CSDN博客
其中与初值有关的操作有,设置导入一个启发式解决方案的值为初值或部分初值。涉及的方法为cbSetSolution,cbSetSolution ( vars, solution )方法中有两个待输入参数,其中一个vars为需要指定初值的变量,可以为一个,也可以为一个列表的变量;另一个solution则是新解决方案中那些被指定初值的变量的所需值,即vars需要的值。例子代码如下:
# Example usage:
def mycallback(model, where):
if where == GRB.Callback.MIPNODE:
model.cbSetSolution(vars, newsolution)
objval = model.cbUseSolution()
model.optimize(mycallback)
# 如:
if abs(subX[i + j -1].x) < 0.001: # 松弛解中该变量的取值在0附近
model.cbSetSolution(model._X[(i,j)], 0.0) # 将该变量的取值上界设为0
elif abs(subX[i + j-1].x - 1) < 0.001: # 在1附近
model.cbSetSolution(model._X[(i,j)], 1.0)可以继续使用 cbUseSolution()方法来使用被指定初值的vars们立即使用启发式方法计算出一个可行解。
参考文献:
优化求解器 | 求解器加速的高级技能包:MIP模型初始解设置相关操作的超详细解读