操作环境：

MATLAB 2013b

1、算法描述

压缩感知（Compressed Sensing, CS）是一种从稀疏或可压缩信号中重构完整信号的数学理论和技术。下面详细介绍压缩感知和它在OFDM信道估计中的应用。

1. 压缩感知基本概念

在传统采样理论中，为了能够无失真地恢复原始信号，需要按照Nyquist-Shannon采样定理的要求进行采样，即采样率要大于或等于信号的两倍最大频率。而在压缩感知中，即使以低于Nyquist采样率的频率进行采样，也能够恢复出原始信号，但前提是这个信号是稀疏的或者可以在某个基上表示为稀疏的。

压缩感知的核心是通过最优化技术（例如L1范数最小化）恢复出原始信号。

2. OFDM信道估计中的压缩感知

在OFDM（Orthogonal Frequency Division Multiplexing）系统中，信道估计是关键技术之一。由于OFDM信号在时间和频率上具有稀疏特性，因此压缩感知可以用来估计OFDM信道。

当信道的多径效应使其响应在某种基（例如DCT或wavelet基）上呈稀疏或可压缩状态时，可以利用压缩感知进行高效的信道估计。

3. 压缩感知与LS算法对比

优点：

• 效率: 压缩感知可以在更少的观测/采样下完成信道估计，因此可以降低采样复杂性和成本。
• 精确性: 由于压缩感知利用了信号的稀疏特性，它可以在低SNR条件下提供较好的估计性能。

缺点：

• 计算复杂性: 相对于LS等传统方法，压缩感知需要解决优化问题，如L1范数最小化，这通常需要较高的计算复杂性。
• 依赖于稀疏性: 如果信号不是真正的稀疏或可压缩的，那么压缩感知的性能可能会受到影响。

总之，压缩感知为OFDM信道估计提供了一种有效的方法，特别是当信道响应具有稀疏特性时。但需要权衡计算复杂性和估计性能。

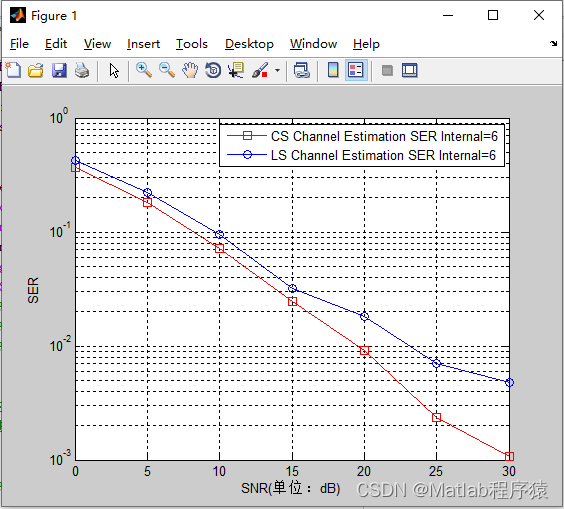
2、仿真结果演示

3、关键代码展示

略

4、MATLAB 源码获取

      V

点击下方名片