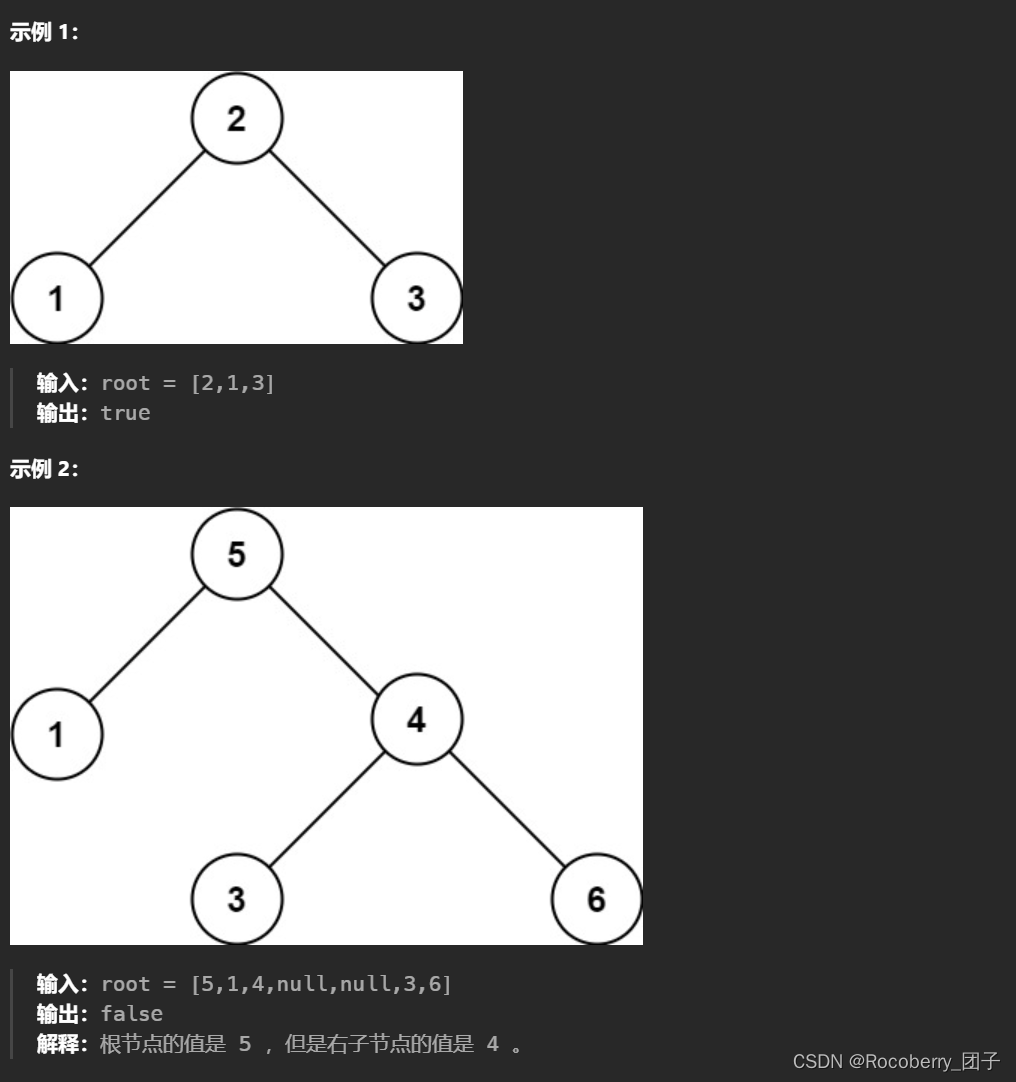
给你一个二叉树的根节点 root ，判断其是否是一个 有效的二叉搜索树。

有效二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数
• 节点的右子树只包含 大于 当前节点的数
• 所有左子树和右子树自身必须也是二叉搜索树
  
  提示：
• 树中节点数目范围在[1, 104] 内
• -$2^{31}$ <= Node.val <= $2^{31}-1$

理解题意：验证搜索二叉树：中序遍历是升序

题解1 递归（学习学习！）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool check(TreeNode* root, long low, long high){
        if(! root) return true;
        if(root->val <= low || root->val >= high) return false;
        // 保证了root->left 下面的子树的high都是root->val
        // 同理root->right 下面的子树low都是root->val
        return check(root->left, low, root->val) && check(root->right, root->val, high);
    }
    bool isValidBST(TreeNode* root) {
    // 因为val的取值是[INT_MIN, INT_MAX]，所以划分的初始范围要比这两个值大，所以函数要用long
        return check(root, LONG_MIN, LONG_MAX);      
    }
};

题解2 中序遍历（保持升序）

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if(! root) return true;
        stack<TreeNode*> kk;

        long prevalue = LONG_MIN;
        // 中序遍历
        while(root || kk.size()){
            while(root){
                kk.push(root);
                root = root->left;
            }
            root = kk.top();
            kk.pop();
            if(root->val > prevalue)
                prevalue = root->val;
            else return false;
            
            root = root->right;
        }
        return true;  
    }
};