1 概述

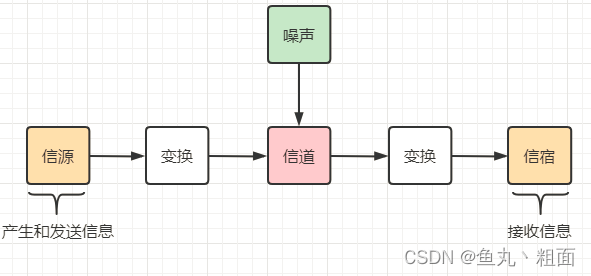
1.1 通信系统模型图

• 通信的目的：传递信息
  

2 信道特性

2.1 信道带宽 W

• 模拟信道： W = f2 - f1（f2 和 f1 分别表示：信道能通过的最高/最低频率，单位：赫兹 Hz）
• 数字信道： W = max(数据传输速率)，单位：比特/秒
• 数据传输速率：每秒钟 能够传输的 二进制数据位数，单位：比特/秒（bit/s、b/s 或 bps）
  
• 码元：承载信息量的基本信号单位。一个码元就是一个脉冲信号，可携带 n bit 数据
• 码元速率（波特率）：单位时间内通过信道传输的码元个数。若信号码元宽度（脉冲周期）为 T 秒，则码元速率 B = 1/T ，单位：波特 Baud
• 一个码元携带信息量 n 位 与 码元种类数 N 的关系：$n=lo{g}_{2}N$

2.2 奈奎斯特定理 - 无噪音

• 奈奎斯特定理（Nyquist’s Theorem）：在一个 理想的（没有噪音环境） 的信道中，若信道带宽为 W，则最大码元速率：B = 2W（Baud）
• 极限数据传输速率： $R=B\ast lo{g}_{2}N=2W\ast lo{g}_{2}N$ （码元速率 * 每个码元携带的信息量）

2.3 香农定理 - 有噪音

• 香农定理（Shannon’s Theorem）：在一个 噪声信道 的 极限数据传输速率 和 带宽 之间的关系
• 极限数据传输速率：$C=Wlo{g}_2(1+\frac{S}{N})$
• 分贝与信噪比：$dB=10lo{g}_{10}\frac{S}{N}$
• 其中，W：带宽，S：信号的平均功率，N：噪声的平均功率，$\frac{S}{N}$：信噪比

2.4 带宽、码元速率、数据速率 关系梳理

3 网工软考真题

// 2010年 下半年 上午
[例1]设信道采用 2DPSK 调制，码元速率为 300 波特，则最大的数据速率为（）b/s
     A.300     B.600     C.900     D.1200

【解析：参考答案 A】

• 2DPSK：二进制差分相移键控，表示：N = 2
• 没说噪音，采用奈奎斯特定理：$R=B\ast lo{g}_{2}N=300\ast lo{g}_{2}2=300bps$

// 2015年 下半年 上午
[例2]设信号的波特率为 500 Baud，采用幅度相位符合调制技术，由 4 种幅度
     和 8 种相位组成 16 种码元，则信道的数据速率为（）？
     A.500b/s   B.1000b/s   C.2000b/s   D.4800b/s

【解析：参考答案 C】

• 没说噪音，采用奈奎斯特定理：$R=B\ast lo{g}_{2}N=500\ast lo{g}_{2}16=2000bps$

// 2018年 下半年 上午
[例3]设信道带宽为 1000Hz，信噪比为 30dB，则信道最大速率为（）b/s
     A.10000   B.20000   C.30000   D.40000

【解析，参考答案 A】

• 信噪比 => 有噪音 => 香农定理：$C=Wlo{g}_2(1+S/N)，dB=10lo{g}_{10}(S/N)$
• 信噪比 = $30dB=10lo{g}_{10}(S/N)$ => $S/N=10^3=1000$
• 最大速率 $C=1000lo{g}_2(1+1000)\approx 10000，（2^{10}=1024）$

// 2017年 上半年 上午
[例4] 电话信道频率为 0~4KHz，若信噪比为 30dB，则信道容量为（）kb/s
      要达到此容量，至少需要（）个信号状态
      A.4     B.20     C.40     D.80
      A.4     B.8      C.16     D.32 

【解析，参考答案：C、D】

• 信噪比 = $30dB=10lo{g}_{10}(S/N)$ => $S/N=10^3=1000$
• 香农定理：$C=Wlo{g}_2(1+S/N)=10W$，其中 W = 4kHz - 0kHz = 4kHz，故 C = 10 * 4 = 40 kb/s
• 至少（奈奎斯特定理）：$R=Blo{g}_{2}N=2W\ast lo{g}_{2}N=40k$ => $N=2^5=32$