【数据结构】海量数据处理

前言

海量数据处理是指基于海量数据的存储和处理，正因为数据量太大，所以导致要么无法在短时间内迅速处理，要么无法一次性装入内存。

对于时间问题，就可以采用位图、布隆过滤器等数据结构来解决。
对于空间问题，就可以采用哈希切割等方法，将大规模的数据转换成小规模的数据逐个击破。

位图相关

题目一：给定100亿个整数，设计算法找到只出现一次的整数。

我们标记整数时可以将其分为三种状态：

出现0次。
出现1次。
出现2次及以上。

一个位只能表示两种状态，而要表示三种状态我们至少需要用两个位，因此我们可以开辟两个位图，这两个位图的对应位置分别表示该位置整数的第一个位和第二个位。

我们可以将着三种状态分别定义为00、01、10，此时当我们读取到重复的整数时，就可以让其对应的两个位按照00→01→10的顺序进行变化，最后状态是01的整数就是只出现一次的整数。

为了方便演示，下面我们直接从vector中读取若干整数进行模拟处理：

#include <assert.h>
#include <bitset>
#include <iostream>
#include <vector>
using namespace std;

int main() {
    //此处应该从文件中读取100亿个整数
    vector<int> v{12, 33, 4, 2, 7, 3, 32, 3, 3, 12, 21};
    //在堆上申请空间
    bitset<4294967295> *bs1 = new bitset<4294967295>;
    bitset<4294967295> *bs2 = new bitset<4294967295>;
    for (auto e: v) {
        if (!bs1->test(e) && !bs2->test(e)) {//00->01
            bs2->set(e);
        } else if (!bs1->test(e) && bs2->test(e)) {//01->10
            bs1->set(e);
            bs2->reset(e);
        } else if (bs1->test(e) && !bs2->test(e)) {//10->10
            //不做处理
        } else {//11（理论上不会出现该情况）
            assert(false);
        }
    }

    for (size_t i = 0; i < 4294967295; i++) {
        if (!bs1->test(i) && bs2->test(i)) {
            //01
            cout << i << endl;
        }
    }
    return 0;
}

题目二：给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件的交集？

方案一：（一个位图需要512M内存）

依次读取第一个文件中的所有整数，将其映射到一个位图。
再读取另一个文件中的所有整数，判断在不在位图中，在就是交集，不在就不是交集。

方案二：（两个位图刚好需要1G内存，满足要求）

依次读取第一个文件中的所有整数，将其映射到位图1。
依次读取另一个文件中的所有整数，将其映射到位图2。
将位图1和位图2进行与操作，结果存储在位图1中，此时位图1当中映射的整数就是两个文件的交集。

说明一下：对于32位的整型，无论待处理的整数个数是多少，开辟的位图都必须有2的32次方个比特位，也就是512M，因为我们要保证每一个整数都能够映射到位图当中，因此这里位图的空间消耗是固定的。

题目三：一个文件有100亿个整数，1G内存，设计算法找到出现次数不超过2次的所有整数。

该题目和题目一的方法是一样的，在该题目中我们标记整数时可以将其分为四种状态：

出现0次。
出现1次。
出现2次。
出现2次以上。

一个整数要表示四种状态也是只需要两个位就够了，此时当我们读取到重复的整数时，就可以让其对应的两个位按照00→01→10→11的顺序进行变化，最后状态是01或10的整数就是出现次数不超过2次的整数。

#include <bitset>
#include <iostream>
#include <vector>
using namespace std;

int main() {
    vector<int> v{12, 33, 4, 2, 7, 3, 32, 3, 3, 12, 21};
    //在堆上申请空间
    bitset<4294967295> *bs1 = new bitset<4294967295>;
    bitset<4294967295> *bs2 = new bitset<4294967295>;
    for (auto e: v) {
        if (!bs1->test(e) && !bs2->test(e)) {//00->01
            bs2->set(e);
        } else if (!bs1->test(e) && bs2->test(e)) {//01->10
            bs1->set(e);
            bs2->reset(e);
        } else if (bs1->test(e) && !bs2->test(e)) {//10->11
            bs2->set(e);
        } else {//11->11
            //不做处理
        }
    }

    for (size_t i = 0; i < 4294967295; i++) {
        if ((!bs1->test(i) && bs2->test(i)) || (bs1->test(i) && !bs2->test(i))) {
            //01或10
            cout << i << endl;
        }
    }
    return 0;
}

布隆过滤器相关

给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件的交集？给出近似算法

题目要求给出近视算法，也就是允许存在一些误判，那么我们就可以用布隆过滤器。

先读取其中一个文件当中的query，将其全部映射到一个布隆过滤器当中。
然后读取另一个文件当中的query，依次判断每个query是否在布隆过滤器当中，如果在则是交集，不在则不是交集。

哈希切割相关

给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件的交集？给出精确算法。

还是刚才那道题目，但现在要求给出精确算法，那么就不能使用布隆过滤器了，此时需要用到哈希切分。

首先需要估算一下这里一个文件的大小，便于确定将一个文件切分为多少个小文件。
假设平均每个query为20字节，那么100亿个query就是200G，由于我们只有1G内存，这里可以考虑将一个文件切分成400个小文件。
这里我们将这两个文件分别叫做A文件和B文件，此时我们将A文件切分成了A0_{A399共400个小文件，将B文件切分成了B0}B399共400个小文件。

在切分时需要选择一个哈希函数进行哈希切分，以切分A文件为例，切分时依次遍历A文件当中的每个query，通过哈希函数将每个query转换成一个整型 i (0 ≤ i ≤ 399），然后将这个query写入到小文件Ai当中。对于B文件也是同样的道理，但切分A文件和B文件时必须采用的是同一个哈希函数。
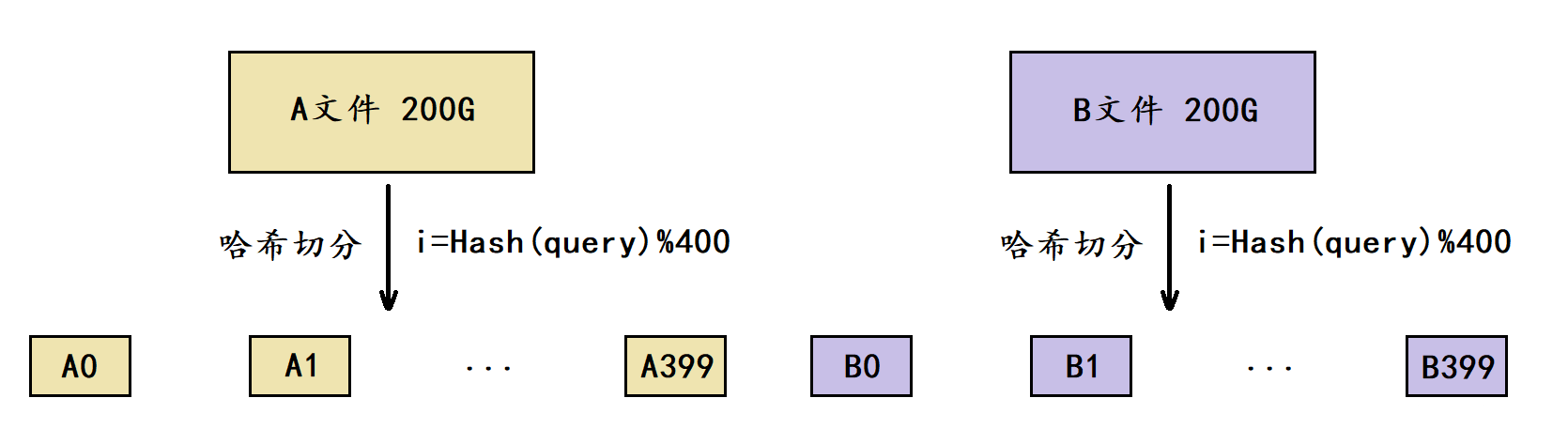
在这里插入图片描述

由于切分A文件和B文件时采用的是同一个哈希函数，因此A文件与B文件中相同的query计算出的 i ii 值都是相同的，最终就会分别进入到Ai和Bi文件中，这也是哈希切分的意义。

因此我们就只需要分别找出A0与B0的交集、A1与B1的交集、…、A399与B399的交集，最终将这些交集和起来就是A文件和B文件的交集。

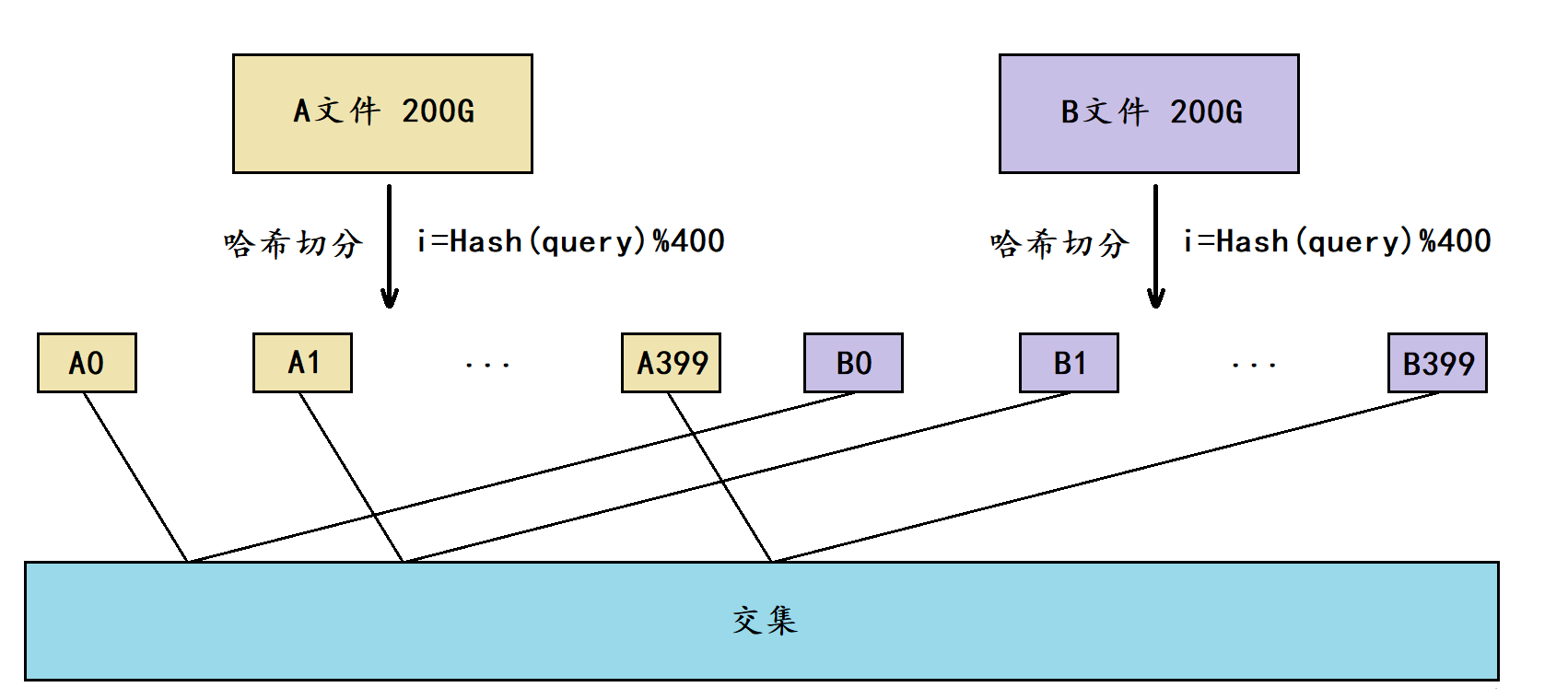
在这里插入图片描述

那各个小文件之间又应该如何找交集呢？

经过切分后理论上每个小文件的平均大小是512M，因此我们可以将其中一个小文件加载到内存，并放到一个set容器中，再遍历另一个小文件当中的query，依次判断每个query是否在set容器中，如果在则是交集，不在则不是交集。
当哈希切分并不是平均切分，有可能切出来的小文件中有一些小文件的大小仍然大于1G，此时如果与之对应的另一个小文件可以加载到内存，则可以选择将另一个小文件中的query加载到内存，因为我们只需要将两个小文件中的一个加载到内存中就行了。
但如果两个小文件的大小都大于1G，那我们可以考虑将这两个小文件再进行一次切分，将其切成更小的文件，方法与之前切分A文件和B文件的方法类似。
本质这里在进行哈希切分时，就是将这些小文件看作一个个的哈希桶，将大文件中的query通过哈希函数映射到这些哈希桶中，如果是相同的query，则会产生哈希冲突进入到同一个小文件中。

给一个超过100G大小的log file，log中存着IP地址，设计算法找到出现次数最多的IP地址？如何找到top K的IP？如何直接用Linux系统命令实现？

该题目同样需要用到哈希切分，切分步骤如下：

我们将这个log file叫做A文件，由于A文件的大小超过100G，这里可以考虑将A文件切分成200个小文件。
在切分时选择一个哈希函数进行哈希切分，通过哈希函数将A文件中的每个IP地址转换成一个整型 i (0 ≤ i ≤ 199），然后将这个IP地址写入到小文件Ai当中。
由于哈希切分时使用的是同一个哈希函数，因此相同的IP地址计算出的i值是相同的，最终这些相同的IP地址就会进入到同一个Ai小文件当中。

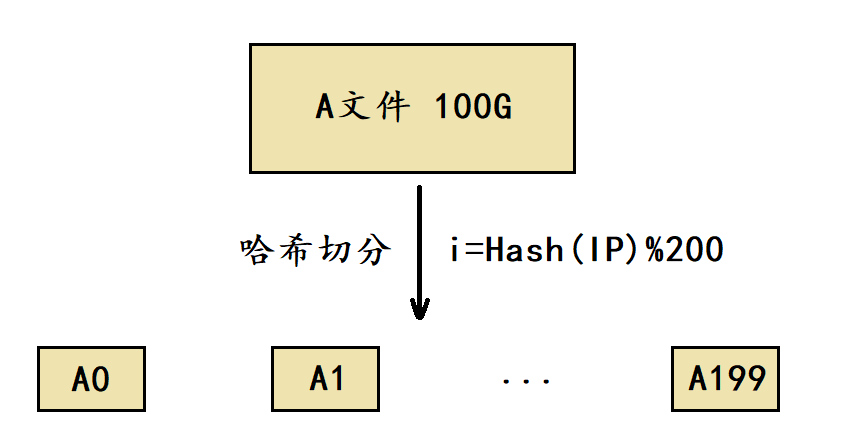
在这里插入图片描述

经过哈希切分后得到的这些小文件，理论上就能够加载到内存当中了，如果个别小文件仍然太大那可以对其再进行一次哈希切分，总之让最后切分出来的小文件能够加载到内存。

现在要找到出现次数最多的IP地址，就可以分别将各个小文件加载到内存中，然后用一个map<string, int>容器统计出每个小文件中各个IP地址出现的次数，然后比对各个小文件中出现次数最多的IP地址，最终就能够得到log file中出现次数最多的IP地址。
如果要找到出现次数top K的IP地址，可以先将一个小文件加载到内存中，选出小文件中出现次数最多的K个IP地址建成一个小堆，然后再依次比对其他小文件中各个IP地址出现的次数，如果某个IP地址出现的次数大于堆顶IP地址出现的次数，则将该IP地址与堆顶的IP地址进行交换，然后再进行一次向下调整，使其仍为小堆，最终比对完所有小文件中的IP地址后，这个小堆当中的K个IP地址就是出现次数top K的IP地址。

件加载到内存中，选出小文件中出现次数最多的K个IP地址建成一个小堆，然后再依次比对其他小文件中各个IP地址出现的次数，如果某个IP地址出现的次数大于堆顶IP地址出现的次数，则将该IP地址与堆顶的IP地址进行交换，然后再进行一次向下调整，使其仍为小堆，最终比对完所有小文件中的IP地址后，这个小堆当中的K个IP地址就是出现次数top K的IP地址。