任务概念
- 什么是任务
任务是一个参数为指针,无法返回的函数,函数体为死循环不能返回 - 任务的实现过程
每个任务是独立的,需要为任务分别分配栈称为任务栈,通常是预定义的全局数组,也可以是动态分配的一段内存空间,都是在RAM区。
任务栈的定义:类型是StackType_t 例如StackType_t Task1Stack[128]是定义了一个名为Task1Stack,大小为128字,512字节的栈。
任务控制块:存放着任务栈指针,任务名称,形参;通过任务控制块控制任务的运行。在task文件里面定义了任务控制块的结构体TCB_t。裁剪后的任务控制块:其中ListItem_t列表项

在List文件中定义了列表xLIST。列表的第一个和最后一个是检查列表完整性的,默认不开启,暂时用不到,第二个是记录列表项的数量,第三个是列表的记录当前列表项的索引,可以通过这个来遍历列表(类似链表),第四个指定最后一个列表项。

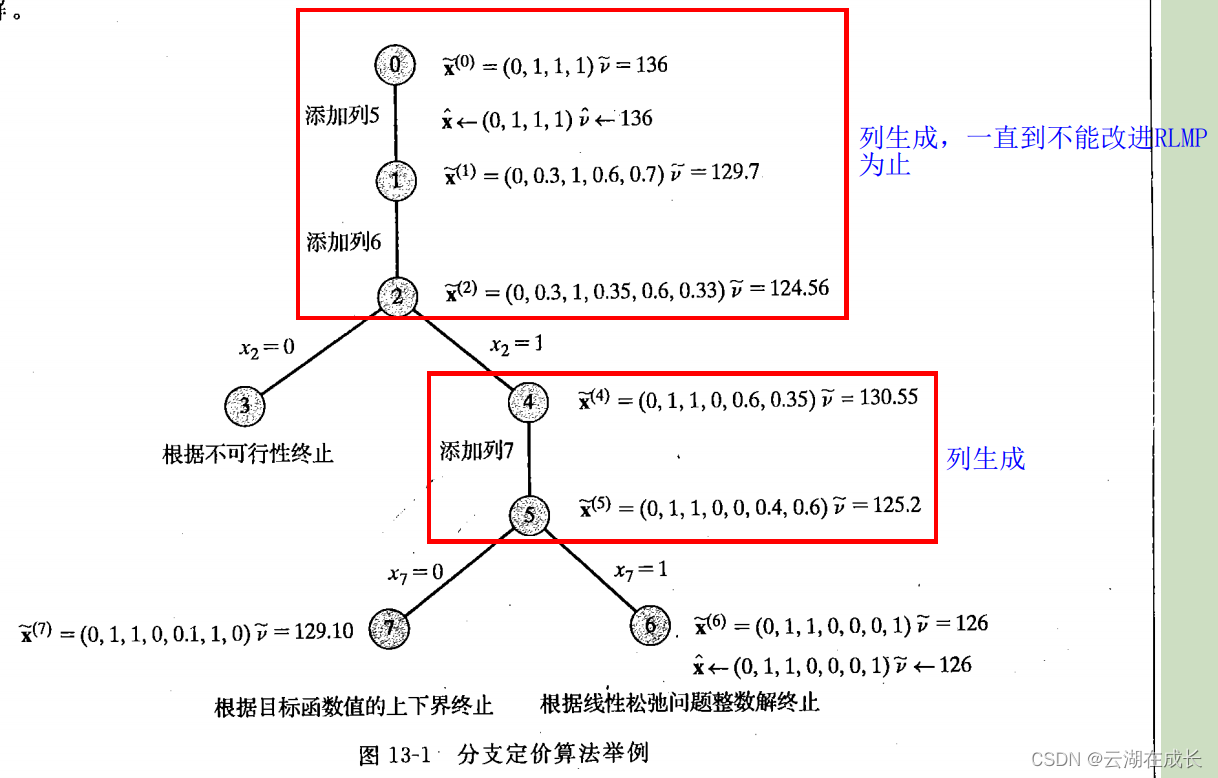
列表项:xLIST_ITEM,第一个和最后一个元素是检查列表项完整性的,默认不开启。第二个是列表项保存的值,第三个是指向下一个列表项,第四个是指向上一个列表项,第五个指向此列表项的拥有者(谁创建的),第六个是列表项当前存在的列表(此列表项在哪里)。
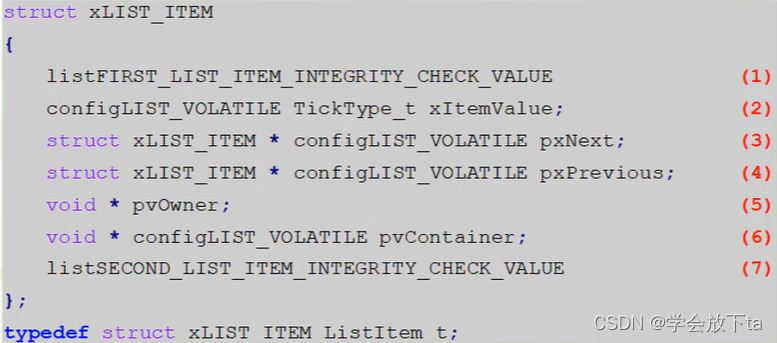
迷你列表项xMINI_LIST_ITEM:第一个是检查迷你列表项的完整性,暂时没用到,第二个是迷你列表项中的值,第三个是指向下一个列表项,第四个是指向上一个列表项。实际上就是列表项少了一个元素,因为有些场景不需要列表项全部的元素即可完成功能,为了节省内存就用迷你列表项。
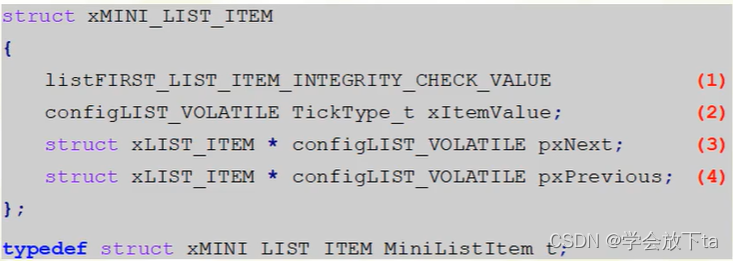
列表的初始化:列表的最后一个列表项是不计入列表项数量的,相当于头结点链表的头结点。开始只有一个end列表项,所以(1)pxIndex索引指向end。(2)值默认初始化为全f。(3)(4)一个项的上下一项都是指向自己,(5)(6)列表项个数初始化为0.剩下两项是初始化列表完整性检查字段。
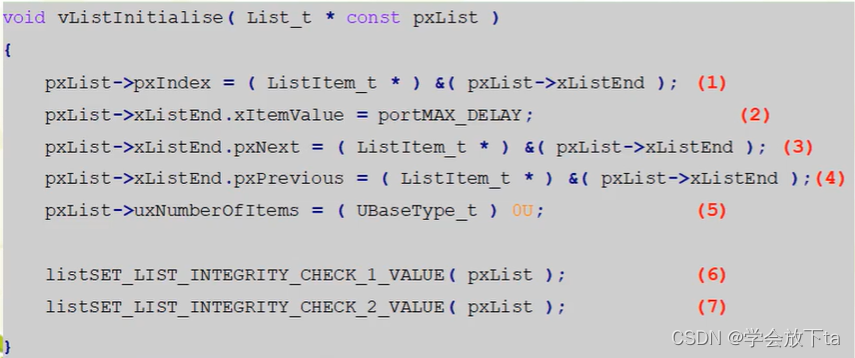
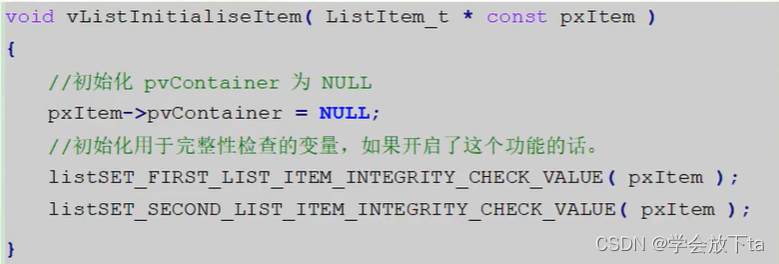
列表项的初始化只需要把pvContainer初始化为NULL就行,其他函数会初始化如任务创建函数。
插入列表项函数源码介绍:
void vListInsert( List_t * const pxList, ListItem_t * const pxNewListItem )
{
ListItem_t *pxIterator;
const TickType_t xValueOfInsertion = pxNewListItem->xItemValue;//根据值选择插入位置
/* Only effective when configASSERT() is also defined, these tests may catch
the list data structures being overwritten in memory. They will not catch
data errors caused by incorrect configuration or use of FreeRTOS. */
listTEST_LIST_INTEGRITY( pxList );//列表完整性检查断言实现,可不看
listTEST_LIST_ITEM_INTEGRITY( pxNewListItem );
/* Insert the new list item into the list, sorted in xItemValue order.
If the list already contains a list item with the same item value then the
new list item should be placed after it. This ensures that TCB's which are
stored in ready lists (all of which have the same xItemValue value) get a
share of the CPU. However, if the xItemValue is the same as the back marker
the iteration loop below will not end. Therefore the value is checked
first, and the algorithm slightly modified if necessary. */
if( xValueOfInsertion == portMAX_DELAY )//如果等于最大值就直接插到最后
{
pxIterator = pxList->xListEnd.pxPrevious;
}
else
{
/* *** NOTE ***********************************************************
If you find your application is crashing here then likely causes are
listed below. In addition see http://www.freertos.org/FAQHelp.html for
more tips, and ensure configASSERT() is defined!
http://www.freertos.org/a00110.html#configASSERT
1) Stack overflow -
see http://www.freertos.org/Stacks-and-stack-overflow-checking.html
2) Incorrect interrupt priority assignment, especially on Cortex-M
parts where numerically high priority values denote low actual
interrupt priorities, which can seem counter intuitive. See
http://www.freertos.org/RTOS-Cortex-M3-M4.html and the definition
of configMAX_SYSCALL_INTERRUPT_PRIORITY on
http://www.freertos.org/a00110.html
3) Calling an API function from within a critical section or when
the scheduler is suspended, or calling an API function that does
not end in "FromISR" from an interrupt.
4) Using a queue or semaphore before it has been initialised or
before the scheduler has been started (are interrupts firing
before vTaskStartScheduler() has been called?).
**********************************************************************/
for( pxIterator = ( ListItem_t * ) &( pxList->xListEnd ); pxIterator->pxNext->xItemValue <= xValueOfInsertion; //否则找出位置pxIterator = pxIterator->pxNext ) /*lint !e826 !e740 The mini list structure is used as the list end to save RAM. This is checked and valid. */
{
/* There is nothing to do here, just iterating to the wanted
insertion position. */
}
}
pxNewListItem->pxNext = pxIterator->pxNext;//上面确定了pxIterator就是该插入的位置,但是只是确定了pxIterator->pxNext,所以这里先赋值pxNext
pxNewListItem->pxNext->pxPrevious = pxNewListItem;//把该位置的下一项的前一项改为插入项
pxNewListItem->pxPrevious = pxIterator;//把pxIterator赋给该位置的上一项(重点)
pxIterator->pxNext = pxNewListItem;//把该位置的上一项的下一项改为插入项完成了双向链表的插入
/* Remember which list the item is in. This allows fast removal of the
item later. */
pxNewListItem->pvContainer = ( void * ) pxList;//添加列表项的位置是这个列表
( pxList->uxNumberOfItems )++;//项数+1
}
列表遍历过程:从第一个(end->next)开始,如果pxIterm->next不等于end继续遍历,如果等于end则跳过end回到第一个就完成了一次遍历。