这个题目重复看了三四遍讲解,才完全搞懂计算过程,特此记录

解析
磁头不会停止旋转
单缓冲区:读取完一个物理块后,只有等该物理块处理完成,才能继续读取后面的物理块。
最长时间
摆放顺序如下:

从 R0 开始顺序读取,
以 R0 为例,当读取 R0 块的时候,花费时间 3ms(总读取周期 33ms ,共 11 个周期),磁头从 R0 开始处,到达 R0 结束处。

由于单缓冲区原因,只能等 R0 被处理完后,才能继续读取 R1。
处理 R0,花费 3ms,此时磁头已经转到 R2 的开始处( R1 的结束处)。
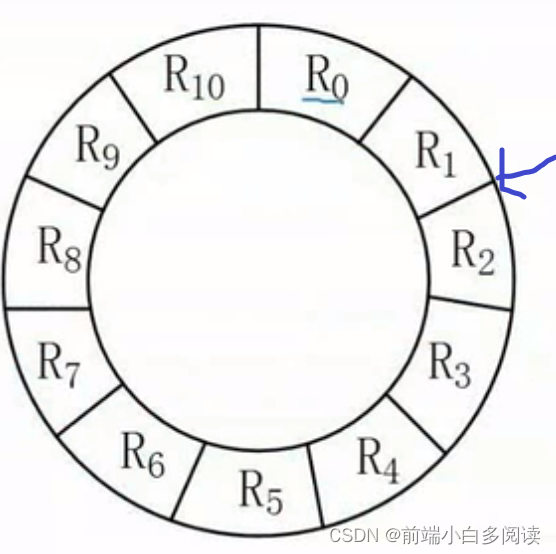
只有再从 R2 的开始处转到 R1 的结束处才能读取到 R1。所以读取 R0 的完整花费即为 3ms(读取 R0 的数据) + 33ms(处理 R0 的 3ms + 从 R2 的开始处转到 R1 的开始处的 30ms) = 36ms
R0 ... R9 全是如此,所以 36ms * 10 = 360ms
当 R9 的周期完成,此时磁头正好处在 R10 的开头处,所以 R10 花费的时间为 3ms(读取 R10) + 3ms(处理 R10) = 6ms
全部时间为 360ms + 6ms = 366ms
最短时间
从最长时间,我们可以得到,每次由于处理时间,磁头都会挪到目前处理磁块的后面第二块,所以我们可以按以下方式摆放。
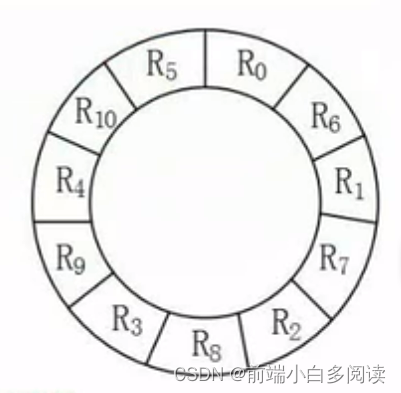
读取并处理完成 R0,此时磁头正好位于 R1 开始处,其余磁块同理,所以总时间为 3ms(读取时间) + 3ms(处理时间) = 6ms