为何要研究张量？

--主要原因是几何。

Tensors = Geometry

了解张量后，可深入了解几何的工作原理

几何的一个例子：爱因斯坦广义相对论中的时空几何 

时空是如何弯曲的，宇宙是如何膨胀的。          要从数学上理解这两个问题，需要张量。

爱因斯坦的场方程：

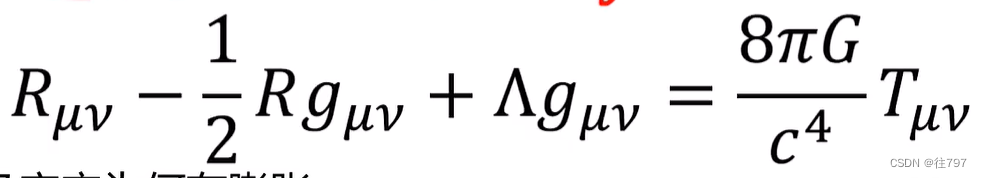
其实上面是含有16个方程。每个符号都是一个张量。

张量的另一个重要的例子是 量子力学，尤其是量子计算：

量子叠加：量子系统可以同时处于两种状态。

量子纠缠：两粒子即使被分离数千公里，它们都能用一种奇特的方式相互影响，使用这种奇特的量子纠缠特性连接起来。

而叠加只是 “线性组合”的一种花哨的说法。

事实证明，在量子力学中，物理状态、物理量子状态  实际上只是向量，因此，可以使用线性组合的方式将更简单的状态组合一起，从而为我们提供更复杂的状态。这就是所有的量子叠加。