算法-动态规划/trie树-单词拆分

1 题目概述

1.1 题目出处

https://leetcode.cn/problems/word-break/description/?envType=study-plan-v2&envId=top-interview-150

1.2 题目描述

2 动态规划

2.1 解题思路

1. dp[i]表示[0, i)字符串可否构建
2. 那么dp[i]可构建的条件是，[0,j)可构建且[j,i)包含在wordDict中
3. 这里你可能会问，那如果是[j,i)不能直接构建，而是有wordDict种的两个单词构建怎么办？其实，因为我们是从低到高构建的动态规划，所以设k > j 且 k <i，那么dp[k] = true，因为dp[j]=true且 [j,k)在wordDict中。那么 [k, i)就是剩下的那个单词了，所以 [j,i)也可以被构建。

2.2 代码

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        // dp[i]表示[0, i)字符串可否构建
        // 那么dp[i]可构建的条件是，[0,j)可构建且[j,i)包含在wordDict中
        boolean[] dp = new boolean[s.length() + 1];
        dp[0] = true;
        Set<String> set = new HashSet<>(wordDict);
        
        for (int i = 1; i <= s.length(); i++) {
            for (int j = 0; j < i; j++) {
                if (dp[j] == true && set.contains(s.substring(j, i))) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[s.length()];
    }
}

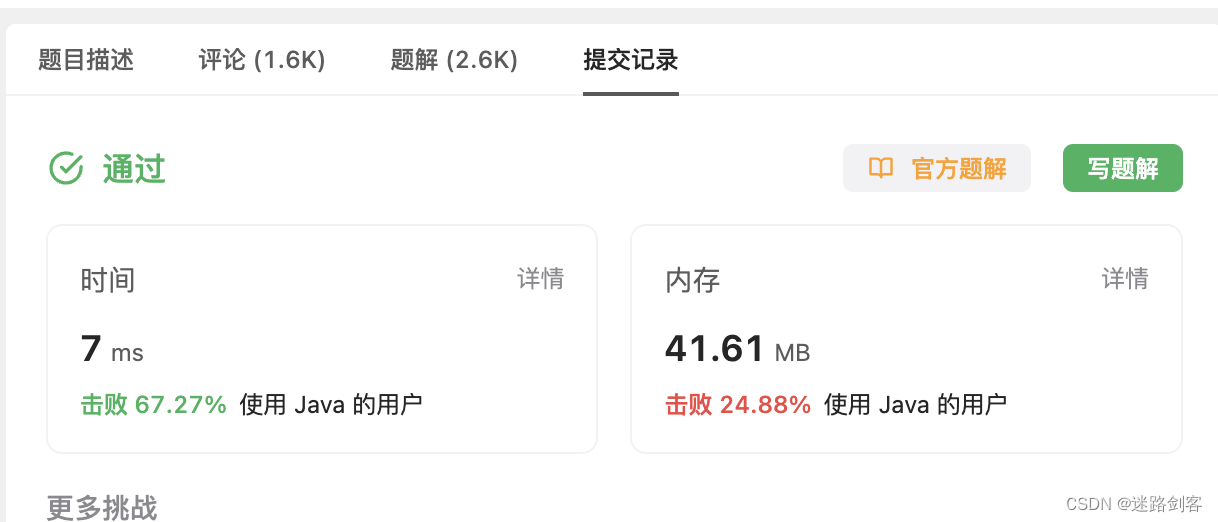
2.3 时间复杂度

O(c*s.length)

2.4 空间复杂度

O( s.length)

3 trie树

3.1 解题思路

1. 将wordDict构建trie树
2. 将s从位置0开始往后匹配查找
3. 如果当前位置能匹配上，继续判断是否是单词结尾，如果是且下一个单词开始的匹配也能成功，就说明能构建，返回true
4. 其他情况继续往后匹配

3.2 代码

class Solution {
    Trie root = new Trie();
    public boolean wordBreak(String s, List<String> wordDict) {
        for (String word : wordDict)
            root.insert(word);
        if (root.find(s, 0)) {
            return true;
        }
        return false;
    }

    class Trie{
        boolean[] no = new boolean[301];
        public Trie[] children = new Trie[26];
        boolean isEnd = false;
        public void insert(String word) {
//                System.out.println(this + " word=" + word);
            if (null == word || word.length() == 0) {
                System.out.println(this + " isEnd = true");
                isEnd = true;
                return;
            }
            int index = word.charAt(0) - 'a';
            Trie child = children[index];
            if (null == child) {
                child = new Trie();
                children[index] = child;
            }
            System.out.println("child=" + child + ", word=" + word);
            child.insert(word.substring(1));
        }
        public boolean find(String s, int i) {
            if (no[i]) {
                return false;
            }
            char firstC = s.charAt(i);
            Trie child = children[firstC - 'a'];
            if (null == child) {
                no[i] = true;
                return false;
            }
            if (child.isEnd) {
                System.out.println("firstC=" + firstC + ", child=" + child);
                if (i + 1 == s.length() || root.find(s, i+1)) {
                    return true;
                }
            }
            no[i] = true;
            if (i + 1 < s.length()) {
                return child.find(s, i+1);
            } else {
                return false;
            }
        }
    }
}

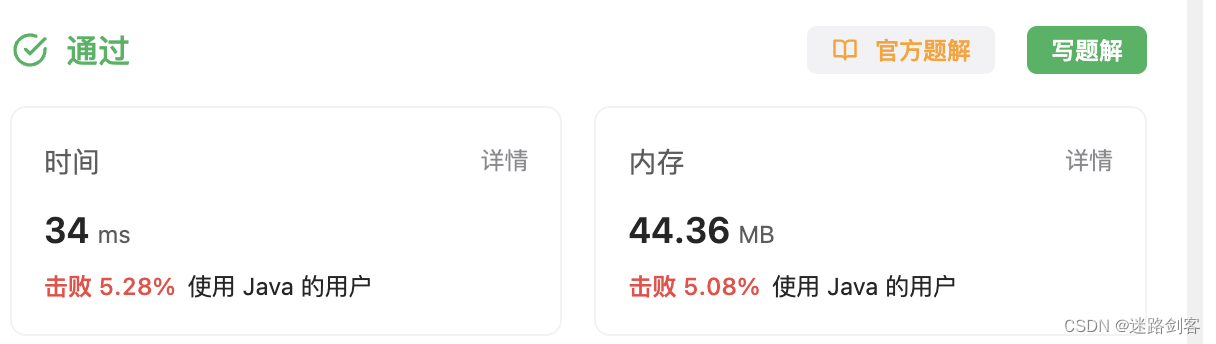
3.3 时间复杂度

3.4 空间复杂度

参考

• 循序渐进5种解法，从字典树trie回溯延伸到动态规划