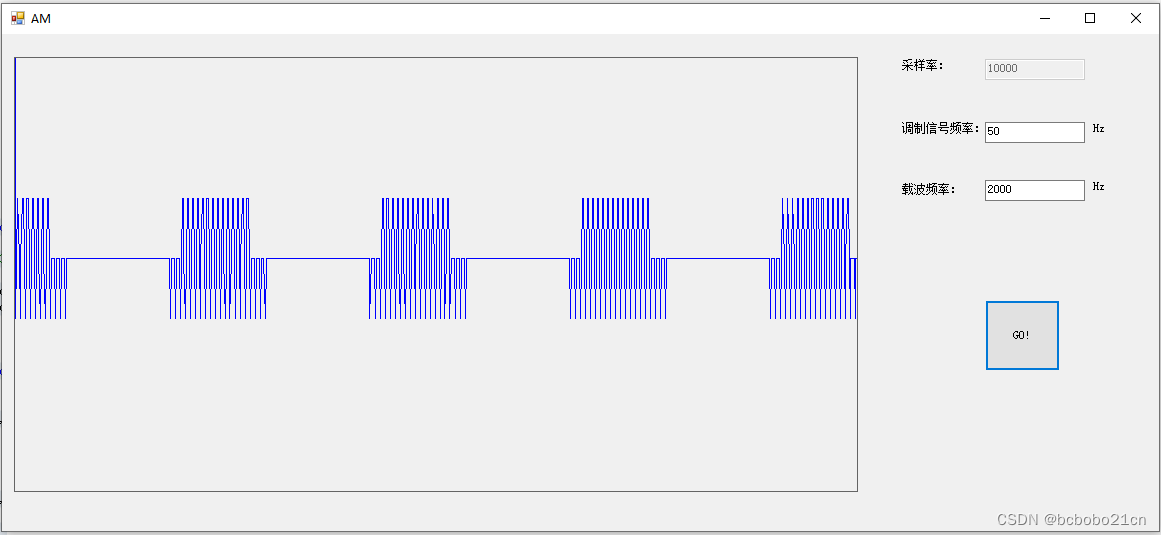
W z学长的apex

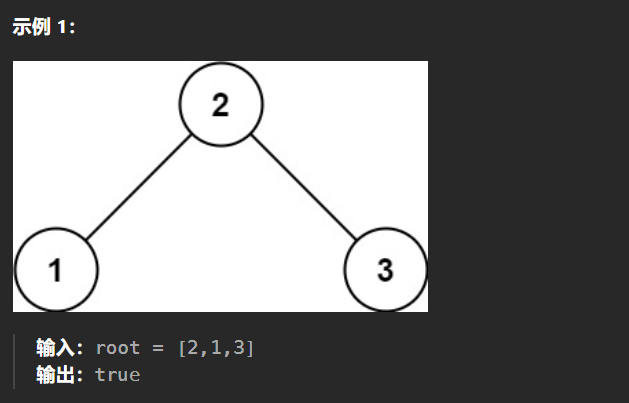
不等于180度的角的个数就是求转折点的个数

而每个y(x)都是一元函数，按照公式每个一元函数的转折点为

s(x)是若干y(x)的叠加，其中一个y(x)有转折点，在对应位置上s(x)也会有转折点

所以所有y(x)函数中不重复的转折点的个数就是答案

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;

typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;

int main()
{
	IOS
	int _;
	cin >> _;
	map<ld, int> mp;
	
	int ans = 0;
	while(_ --)
	{
		ld k, b;
		cin >> k >> b;
		if(k == 0)continue;
		b = -b;
		ld res = b / k;
		if(!mp[res])ans ++;
		mp[res] = 1;
	}
	cout << ans;
	
	return 0;
}

用到了map容器，没学过的可以去学一下，注意开long double，double会被卡精度。

X - tmn学长的贪心

一个小小的思维问题，我们想让差值尽可能的多，其实就是想一种策略：

将a数组从大到小排序

a1 a2 a3 ... an ，使a1 >= a2 >= a3 >= ... >= an 

b对应位之上放1 2 3 .... n

这样就可以保证差值不会重复，因为现在a数组是非递增的，b数组是递增的

一个非递增的数组减一个递增的数组，想当然新的数组不会有重复的元素了

解法不唯一，这是我提供的其中一种。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;

typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;

const int N = 40010;

PII a[N];
int b[N];

bool cmp(PII A, PII B)
{
	return A.first > B.first;
}

void solve()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i ++)
	{
		int x;
		cin >> x;
		a[i] = {x, i};
	}
	
	sort(a + 1, a + 1 + n, cmp);
	
	for(int i = 1; i <= n; i ++)
	{
		int pos = a[i].second;
		b[pos] = i;
	}
	
	for(int i = 1; i <= n; i ++)cout << b[i] << ' ';
	cout << endl;
}

int main()
{
	IOS
	int _;
	cin >> _;
	while(_ --)
	{
		solve();
	}
	
	return 0;
}

用到了自定义sort排序和pair数组

Y - DP?贪心！

也是一个思维问题：怎样让分的段尽可能多

从前往后遍历，每到一个数就找前面有无能与它配对的数，如果有就组成一对，最后能产生的对儿数就是答案

思路大概就是这样，对儿与对儿之间的那些数随便归到哪一对儿里去就行，确保每个数都有一个归属就行。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;

typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;

int main()
{
	IOS
	vector<PII> ans;
	int n;
	cin >> n;
	map<int, int> lst;
	int r = 0;
	for(int i = 1; i <= n; i ++)
	{
		int x;
		cin >> x;
		if(lst[x] && lst[x] > r)
		{
			ans.push_back({lst[x], i});
			lst[x] = 0;
			r = i;
		}
		else lst[x] = i;
	}
	
	if(ans.size() == 0)cout << -1 << endl;
	else
	{
		cout << ans.size() << endl;
		if(ans.size() == 1)
		{
			cout << 1 << ' ' << n << endl;
			return 0;
		}
		
		for(int i = 0; i < ans.size(); i ++)
		{
			if(i == 0)
			{
				cout << 1 << ' ' << ans[i].second << endl;
				continue;
			}
			if(i == ans.size() - 1)
			{
				cout << ans[i - 1].second + 1 << ' ' << n << endl;
				continue;
			}
			cout << ans[i - 1].second + 1 << ' ' << ans[i].second << endl;
		}
	}
	
	return 0;
}