只要做C题基本上都会用到相关性分析、一般性检验等！
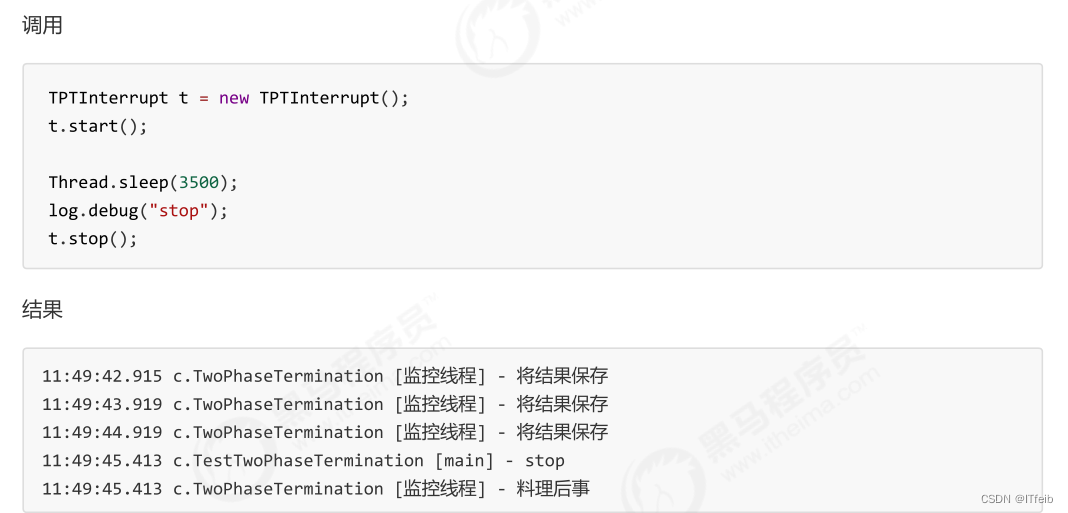
回归模型性能检验
下面讲一下回归模型的性能评估指标，用来衡量模型预测的准确性。下面是每个指标的简单解释以及它们的应用情境：
1. MAPE (平均绝对百分比误差)
- 描述: 衡量模型预测的相对误差。
- 应用情境: 当你想知道模型预测误差相对于实际值的大小时。
2. RMSE (均方根误差)
- 描述: 衡量实际值和预测值之间的偏差。
- 应用情境: 关注所有类型的误差。
3. SSE (残差平方和)
- 描述: 衡量实际值和预测值之间差异的平方和。
4. MSE (均方误差)
- 描述: 衡量实际值和预测值之间差异的平均平方和。
- 应用情境: MSE对大误差更敏感，因为它计算的是误差的平方。如果你的模型有很大的误差，MSE会变得非常大。所以，如果你的任务不能容忍大的误差，使用MSE是有意义的。
5. MAE (平均绝对误差)
- 描述: 衡量实际值和预测值之间差异的平均绝对值。
- 应用情境: MAE对所有误差都是同等敏感的。它不会因为个别的大误差而受到过度影响，因为它不考虑误差的平方。如果你更关心所有类型的误差，而不仅仅是大误差，你可以使用MAE。
6. 
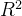(决定系数)
- 描述: 衡量模型解释数据变异的程度。
- 应用情境: 当你想知道模型相对于基准模型（例如，仅使用均值进行预测）的性能时。
结合使用
-
同时使用多个指标：你可以同时使用多个指标来获取模型性能的全面视图。例如，使用
-
与领域知识结合：根据问题的具体上下文和领域知识来选择最合适的指标。例如，在某些情况下，过度估计可能比低估更可取，或者大误差可能比小误差更不可接受。
-
考虑误差类型：不同的指标对不同类型的误差有不同的敏感度（例如，MSE对大误差更敏感，而MAE对所有误差都同等敏感）。
总之，选择哪个指标还取决于具体的应用和业务目标。在实践中，建议使用多个指标，并结合问题的具体背景进行解释和分析。甚至可以自定义损失函数。
%% 一般检验
% 各类检验，除决定系数是1最好，都是0最好
YReal = [1 2 3 4 5];
YPred = [1 2 3 4 5.1];
% 平均绝对百分比误差（MAPE）
mape = mean(abs((YReal - YPred)./YReal));
disp(['MAPE: ' num2str(mape)]);
% 均方根误差（RMSE）
rmse = sqrt(mean((YPred-YReal).^2));
disp(['RMSE: ' num2str(rmse)]);
% 残差平方和（SSE）
sse = sum((YReal - YPred).^2);
disp(['SSE: ' num2str(sse)]);
% 均方误差（MSE）
mse = mean((YReal - YPred).^2);
disp(['MSE: ' num2str(mse)]);
% 平均绝对误差（MAE）
mae = mean(abs(YReal - YPred));
disp(['MAE: ' num2str(mae)]);
% 决定系数（R2-R-Square）
r2 = 1 - (sum((YPred - YReal).^2) / sum((YReal - mean(YReal)).^2));
disp(['R2: ' num2str(r2)]);
相关性分析
相关性分析简介
相关性分析是统计学和数据分析中常用的一种技术，主要用于研究两个或多个变量之间是否存在某种关系（即它们是否相关）。这种关系可以是线性的，也可以是非线性的。通过相关性分析，我们可以量化两个变量之间的关系的强度和方向。
Pearson相关系数
-
使用条件:
- 连续变量: Pearson相关系数只适用于连续变量。
- 线性关系: 变量间的关系应该是线性的。判断变量间
- 正态分布: 数据应该近似或严格符合正态分布。所以需要进行正态性检验，在数据预处理篇作者讲过。
-
应用场景:
- 用于衡量两个连续变量之间的线性相关性。
- 在科学研究、金融分析和社会科学等领域中广泛应用。
Kendall相关系数
-
使用条件:
- 序列数据: 适用于测量序列数据之间的关系。
- 非线性关系: 可用于非线性关系。
-
应用场景:
- 用于衡量两个序列变量之间的相关性。
- 在社会科学、经济学和生物学等领域中应用。
Spearman相关系数
-
使用条件:
- 序列数据: 适用于测量序列数据之间的关系。
- 非线性关系: 可用于非线性关系。
- 不需正态分布: 不需要数据遵循正态分布。
-
应用场景:
- 用于衡量两个序列变量之间的相关性。
- 在许多不同领域中广泛应用，例如心理学和教育研究。
指标选择
再明确一下，相关性分析指标的选择不是随随便便的，一定要分析需要的是线性关系还是非线性关系！
如果你的数据是连续的，并且服从正态分布，那么Pearson相关系数是一个不错的选择。
如果你的数据是序列数据或不满足正态分布，那么Kendall或Spearman相关系数可能是更好的选择。
1. Pearson相关系数 (r)
- 相关性类型: 线性相关性
- 描述: Pearson相关系数主要用于测量两个连续变量之间的线性关系的强度和方向。如果两个变量之间的关系是非线性的，Pearson相关系数可能不会检测到这种关系。
2. Kendall相关系数 (τ)
- 相关性类型: 非线性相关性
- 描述: Kendall τ相关系数不仅可以检测线性关系，还可以检测更复杂的非线性关系。它主要用于测量两个序列变量之间的相关性。
3. Spearman相关系数 (ρ)
- 相关性类型: 非线性相关性
- 描述: Spearman ρ也是一种非参数相关系数，它可以测量两个变量之间的单调关系（不一定是线性关系）。
总结:
- 如果研究目的是了解两个变量之间的线性关系，通常使用Pearson相关系数。
- 如果数据是序列或等级数据，或者关系可能是非线性的，那么Spearman或Kendall相关系数可能更合适。
代码示例
%% 相关性分析
clc, clear, close all;
% 列为指标，行为数据
data = rand(10);
% Pearson相关系数
r1 = corr(data, 'type', 'Pearson');
disp(r1);
% Kendall相关系数
r2 = corr(data, 'type', 'Kendall');
disp(r2);
% Spearman相关系数
r3 = corr(data, 'type', 'Spearman');
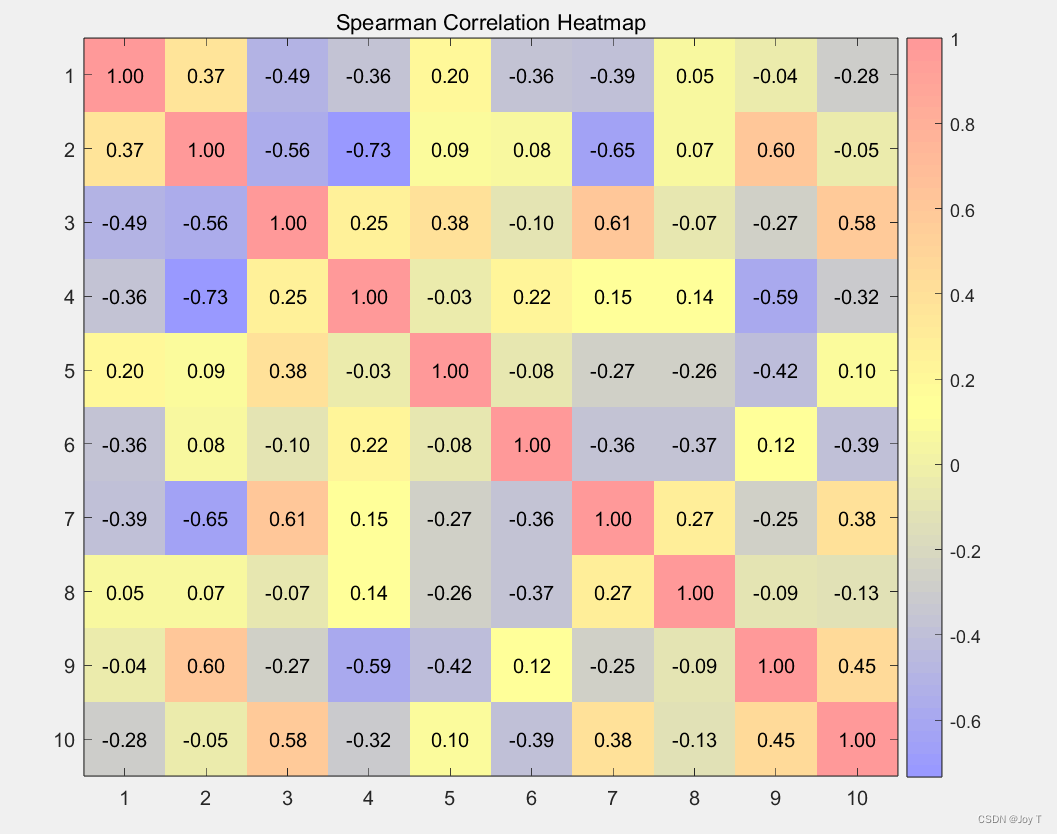
disp(r3);这就求出来了，接下来就是使用r1/r2/r3画相关性分析图了！图可以有很多种选择，但是作者都觉得很丑，所以自己配置了一个小清新的颜色，大家喜欢的话可以拿走哦！
% 设置我自定义的颜色映射
n = 64;
% 从淡蓝色 (0.6, 0.6, 1) 到淡黄色 (1, 1, 0.6)
t1 = linspace(0.6, 1, floor(n/2))';
u1 = linspace(0.6, 1, floor(n/2))';
v1 = linspace(1, 0.6, floor(n/2))';
% 从淡黄色 (1, 1, 0.6) 到淡红色 (1, 0.6, 0.6)
t2 = linspace(1, 1, ceil(n/2))';
u2 = linspace(1, 0.6, ceil(n/2))';
v2 = linspace(0.6, 0.6, ceil(n/2))';
t = [t1; t2];
u = [u1; u2];
v = [v1; v2];
my_colormap = [t,u,v];
figure;
% 创建子图
ax3 = subplot(1, 1, 1);
% 绘制 Spearman 相关系数的热力图
imagesc(ax3, r3);
% 添加颜色条
colorbar(ax3);
% 在每个单元格中添加文本
for i = 1:size(r3, 1)
for j = 1:size(r3, 2)
text(ax3, j, i, sprintf('%.2f', r3(i, j)), ...
'HorizontalAlignment', 'center', ...
'Color', 'k', 'FontSize', 10, 'Parent', ax3);
end
end
% 设置标题
title(ax3, 'Spearman Correlation Heatmap');
% 应用自定义的颜色映射
colormap(ax3, my_colormap);
