数据结构与算法(C语言版)P9---哈夫曼树

1、哈夫曼树的基本概念

（1）路径：从树中一个结点到另一个结点之间的__分支__构成这两个结点间的路径。

（2）__结点的路径长度：__两结点间路径上的分支树。

练习：计算下面二叉树结点之间的路径长度

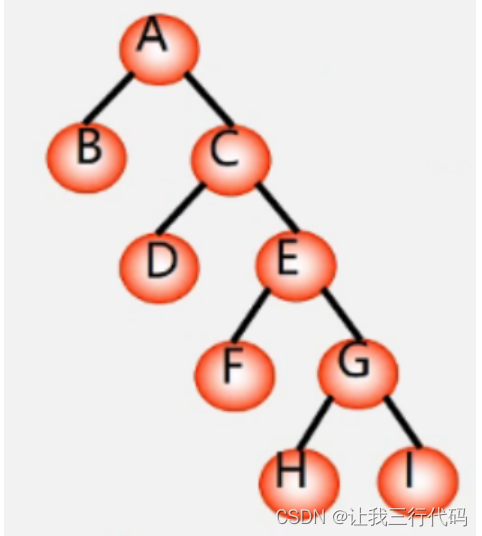
在这里插入图片描述

从结点A到D结点的路径长度为2，原因：A—>C，C—>D。

从C结点到H结点的路径长度为3.原因：C—>E，E—>G，G—>H。

从A到B，C，D，E，F，G，H，I的路径长度分别为1，1，，2，2，3，3，4，4。

（3）__树的路径长度：__从树根到每个结点的路径长度之和。记作：TL。

练习：计算下列二叉树的树路径长度

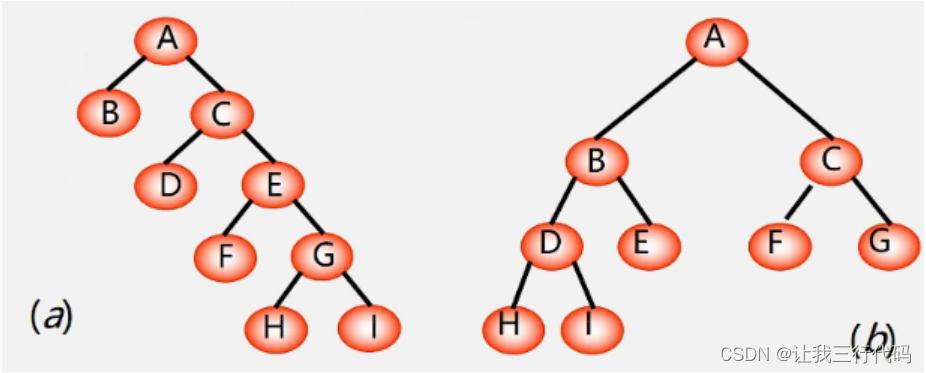
在这里插入图片描述

TL(a)：0+1+1+2+2+3+3+4+4=20

TL(b)：0+1+1+2+2+2+2+3+3=16

结点数目相同的二叉树中，完全二叉树是路径长度最短的二叉树，但路径最短的不一定是完全二叉树。

（4）权（weight）：将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

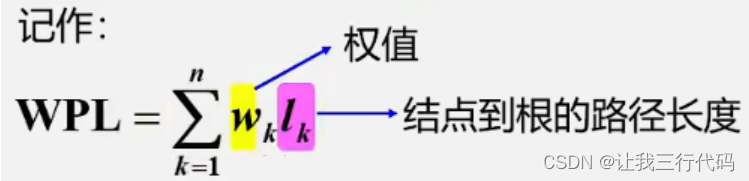
（5）__结点的带权路径长度：__从__跟__结点到该结点之间的__路径长度__与该结点的权的乘积。

（6）__树的带权路径长度：__树中所有叶子节点的带权路径长度之和。

记作：

在这里插入图片描述

__练习一：__有4个结点a，b，c，d。权值分别为7，5，2，4。构造以此4个结点为叶子节点的二叉树如下，现要求求此树的带权路径长度。

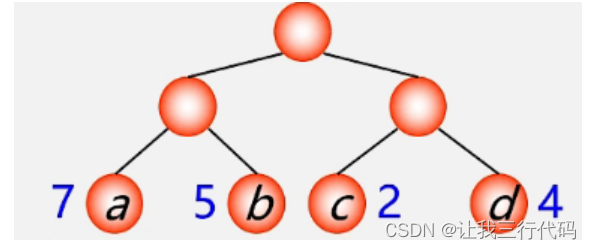
在这里插入图片描述

结算结果：WPL= 7*2 + 5*2 + 2*2 + 4*2 = 14+10+4+8 = 36。

所以此树的带权路径长度为 36。

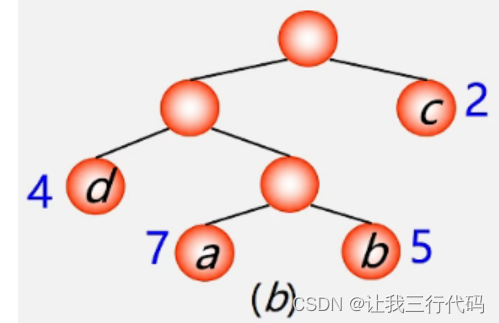
__练习二：__求下列树的带权路径长度

WPL = 4*2 + 2*1 + 7*3 + 3*5 = 8+2+21+15 = 46。

在这里插入图片描述

2、一句话总结哈夫曼树

哈夫曼树就是__最优树，也就是__带权路径长度（WPL）最短的树。

但是有个地方需要注意一下：

【注】：“带权路径长度最短”是在“度相同”的树中比较而得的结果，因此有最优二叉树、最优三叉树之称等等。

所以：最优二叉树，就是带权路径长度（WPL）最短的二叉树。

因为构造这种树的算法是由哈夫曼教授与1952年提出的，所以被称为__哈夫曼树__，相应的算法称为哈夫曼算法。

参考如下图，可以总结哈夫曼树的几个特点：

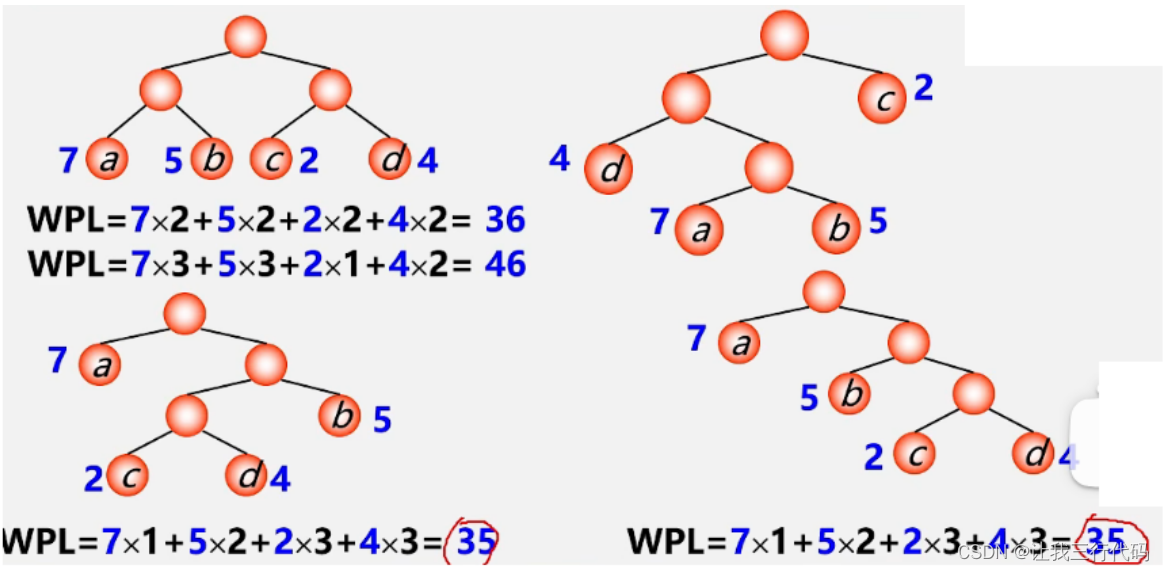
在这里插入图片描述

哈夫曼树的特性：

满二叉树不一定是哈夫曼树。
哈夫曼树中权越大的叶子结点离根越近。
具有相同带权结点的哈夫曼树不唯一。

3、哈夫曼树的构造算法

在上面发现，哈夫曼树中权越大的叶子离根越近。

那我们可以先选择权值小的叶子节点，那最后剩下的就是权值的结点了。

这也是__贪心算法__：构造哈夫曼树时首先选择权值小的叶子结点。

【重点如下】：

哈夫曼算法：

首先根据n个特定的权值{w1,w2,w3,…,wn}构成n棵二叉树的森林，F={T1,T2,…,Tn}，其中Ti只有一个带权为wi的根节点。（简单来说就是：森林里面由n个树，每个树里面只有一个结点，就是根结点。每个根节点对应的权值，就是我们给的。）

这一步可以总结为：构造森林全是根。
在F中选取两颗根节点的权值最小的树作为左右子树，构造一棵新的二叉树，且设置新的二叉树的根节点的权值为其左右子树上根节点的权值之和。

这一步可以总结为：选用两小造新树。
在森林（F）中删除这两棵树，同时将新得到的二叉树加入森林中。

这一步可以总结为：删除两小添新人。
最后重复第二、三步骤，直到森林中只有一棵树为止，这棵树即为哈夫曼树。

口诀：1、构造森林全是根；2、选用两小造新树。

3、删除两小添新人；4、重复2、3剩新书。

下面我们来看个例子：

3.1、示例一：求哈夫曼树

__示例一：__由4个结点a，b，c，d权值分别为7，5，2，4。要求构造哈夫曼树。

（1）构造森林全是根，结果为：

在这里插入图片描述

（2）选用两小造新树，结果为：

将C，D结点作为左右子树，并且此左右子树的根节点是左右子树权值之和。

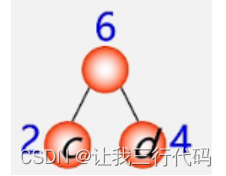
在这里插入图片描述

（3）删除两小添新人。由于结点C，D已经使用了，所以在现在的森林，是如下图：

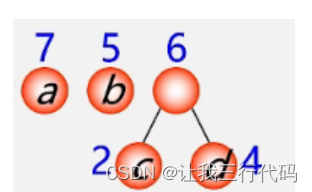
在这里插入图片描述

重复第二、三步骤。

首先第二步：由于现在新的根节点权值为6，那再从森林中单独的根结点中选出权值最小的一个，然后和权值为6的根节点作为新的左右子树即可，如下：

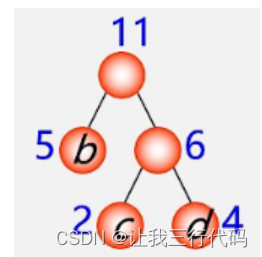
在这里插入图片描述

第三步：现在的森林，如下：

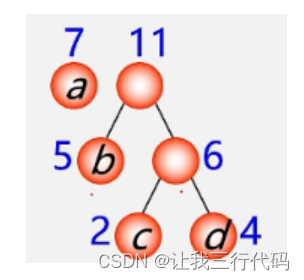
在这里插入图片描述

再重复第二步骤。

首先第二步：由于现在新的根节点权值为11，那再从森林中单独的根结点中选出权值最小的一个，然后和权值为11的根节点作为新的左右子树即可，如下：

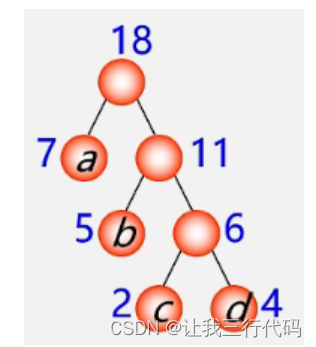
在这里插入图片描述

最后发现森林中树只有一个根结点了，所以哈夫曼树构造完毕。

可以发现：

哈夫曼树中4个带权值的结点都是叶子结点。

哈夫曼树的结点度数只能为0或2，没有度为1的结点。

n个叶子节点的哈夫曼树共有2n-1个结点。

原因：

包含n棵树的森林要经过n-1次合并才能形成哈夫曼树，共产生n-1个新节点。那咋加上原来n个叶子节点，一共就是2n-1个结点。

并且度为0的结点是n个，度为2的结点是n-1个。

3.2、示例二：求哈夫曼树

__示例二：__有5个结点a，b，c，d，e；权值分别为7，5，5，2，4。要求构造哈夫曼树。

（1）构造森林全是根：将每个结点作为单独的树，所以说每个数只有一个结点就是根节点，并且这些由单节点构成的树组成森林。

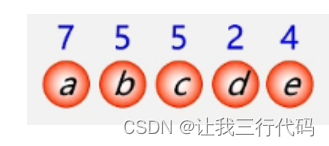
在这里插入图片描述

（2）选用两小造新树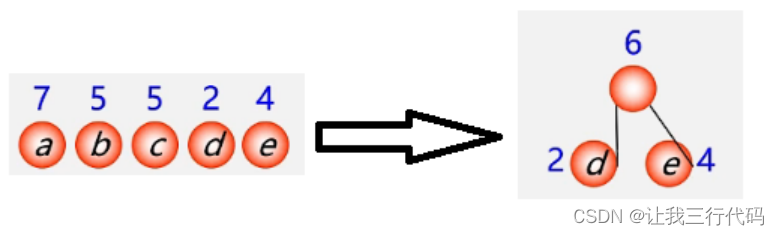：在这里插入图片描述

（3）删除两小添新人：

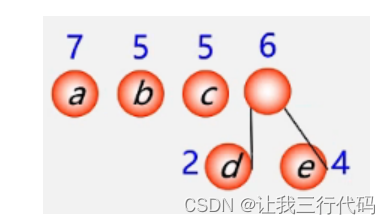
在这里插入图片描述

重复2，3步…

首先是第二步：选用两小造新树

【重点】：我们说第二步要求的是：再森林F中__选取两颗根节点的权值最小的树作为左右子树__

现在那两个结点权值最小呢？就是结点b，c，所以新的左右子树就是b，c结点构成的。这是个要注意的地方，不能把b结点或者c结点和权值为6的结点进行结合成为新的左右子树。

那结果为：

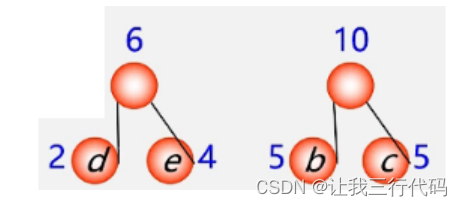
在这里插入图片描述

第三步：删除两小添新人

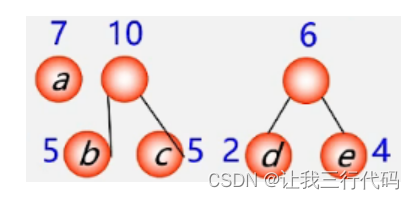
在这里插入图片描述

再重复2，3步…

第二步：选用两小造新树

现在根节点有3个，分别是权重为6，7，10的结点，那需要权值最小的两个结点结合构成新的左右子树，那就是权值为6，7进行结合。

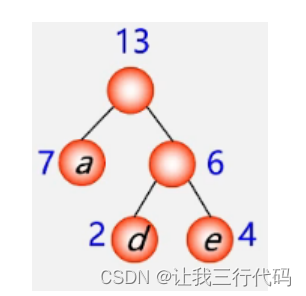
在这里插入图片描述

第三步：删除两小添新人

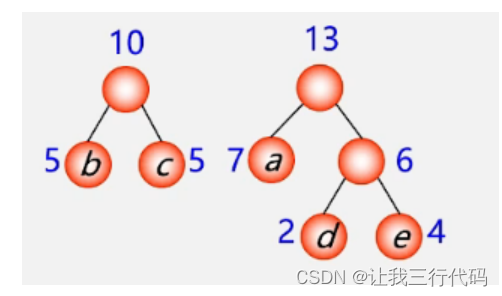
在这里插入图片描述

那到最后就只剩下两个根节点了，那就让它们成为新的左右子树：

在这里插入图片描述

3.3、总结

这里再总结一下：

在哈夫曼树中，初始时有n棵二叉树，要经过n-1次合并最终形成哈夫曼树。
经过n-1次合并产生n-1个新节点，且这个n-1个新节点都是具有两个孩子的分支节点，也就是度为2结点。
可见：哈夫曼树中共有n+n-1=2n-1个结点，且其所有的分支节点的度军部为1，要么为0要么为2。

4、哈夫曼树算法实现

首先哈夫曼树可以使用顺序存储结构，也可以使用链式存储结构。

这里采用顺序存储结构————一维数组，相对来说简单一些。

首先来看结构体定义：

typedef struct
{
    int weight;         //权重值
    int parent,lch,rch;          //双亲结点，左右孩子下标
}HTNode,*HuffmanTree;

如下图表格所示：

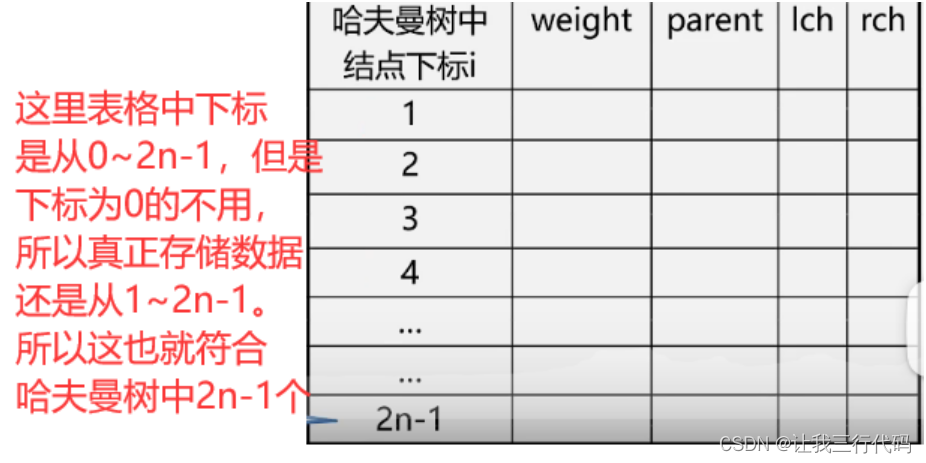
在这里插入图片描述

4.1、看图分析

例，有n=8（有8个根节点），权值为W={7，19，2，6，32，3，21，10}

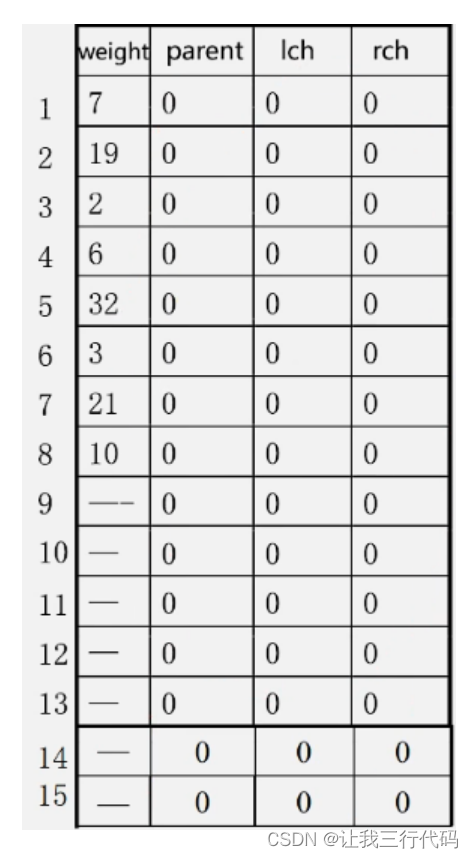
有8个结点，所以最终构成的哈夫曼树共有2*8 - 1= 15个结点。那这里创建一个从0_{16的数组，但是下标为0的数组不用，从下标为1为止开始存储，1}15。

（1）构造结点全是根：由于每个结点在其所在的树中就是根结点，接没有双亲结点，有没有孩子结点，所以在初始化中将其值全部初始化为0。

如下表格：

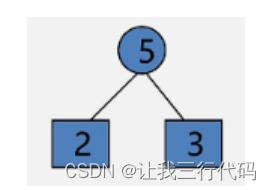
在这里插入图片描述

（2）选用两小造新树，

经过循环找到权重最小的两个结点，下标分别为：3，6。

造新树如下：

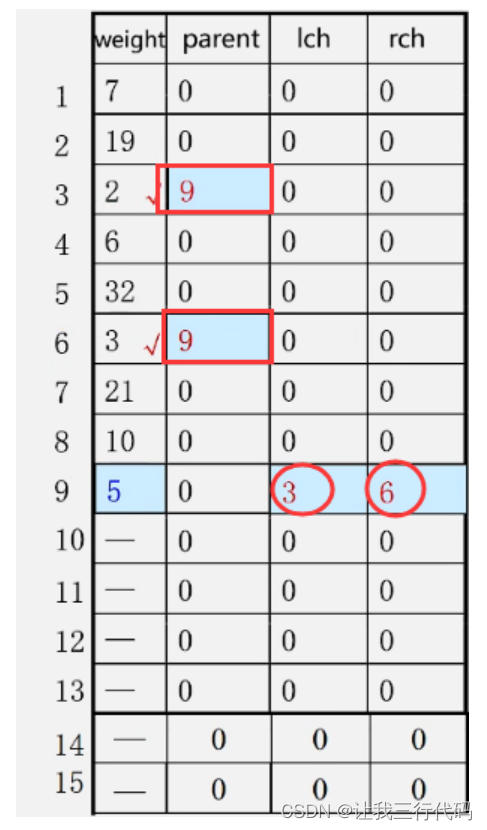
在这里插入图片描述

然后我们把权值为5的结点，存储到数组下表为9处。并且，下标为3，6的结点有双亲结点了，所以，需要在下标3，6的parent处填入双亲结点的下标9。并且双亲结点有左右子树了，所以还需要在下表为9处的lch，rch处填入左右子树的下标，如下图：

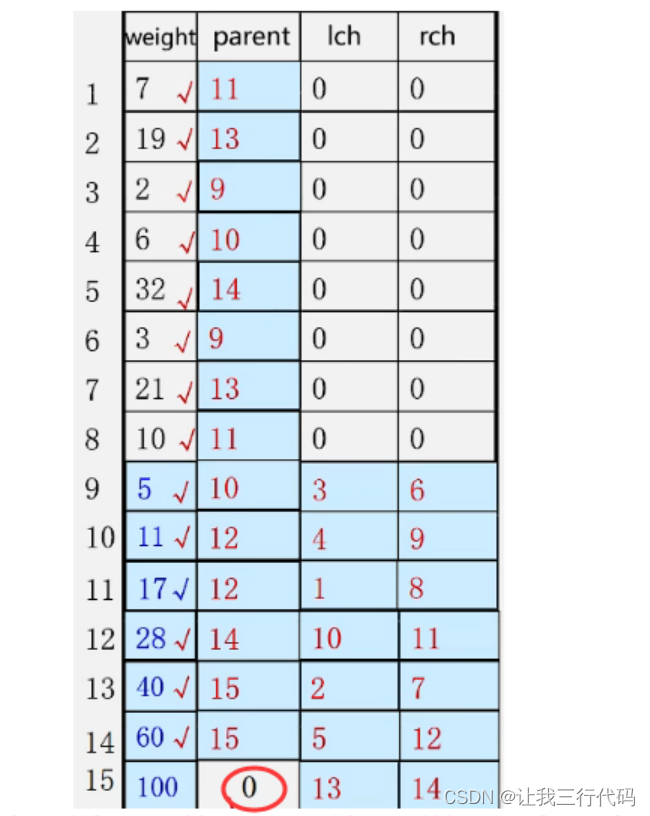
在这里插入图片描述

下面的就重复以上过程即可…

最终结果如下图：

在这里插入图片描述

4.2、具体代码实现

初始化部分：

初始化HT[1,2,3,…,2n-1]：lch=rch=parent=0；
输入初始化n个叶子节点：置HT[1…n]的weight值。

进行合并：

进行以下n-1次合并，依次产生n-1个结点HT[i]，i=n+1/n+2/n+3/…/2n-1。
- a）在HT[1…i-1]中选两个__未被选过__（从parent==0的结点中选）的weight最小的两个结点HT[s1]和HT[s2]，s1、s2为最小结点下标；
- b）修改HT[s1]和HT[s2]的parent值：HT[s1].parent = i；HT[s2].parent=i；
- c）修改新产生的HT[i]：
  - 权值修改：HT[i].weight = HT[s1].weigth+HT[s2].weight;
  - 左右子树修改：HT[i].lch=s1；HT[i].rch=s2；

代码展示：

#define _CRT_SECURE_NO_WARNINGS

#include <stdio.h>
#include <stdlib.h>

typedef struct
{
    int weight;         //权重值
    int parent, lch, rch;          //双亲结点，左右孩子下标
}HTNode, *HuffmanTree;

//筛选出最小和次最小权值的结点
void Select(HuffmanTree* HT, int n, int* s1, int* s2)
{
    ;
}

//构建哈夫曼树
void CreateHuffmanTree(HuffmanTree HT, int n)
{
    int m = 2 * n - 1;         //数组一共2n-1个元素

    if (n <= 1)     
    {
        return;
    }
    //一共2n-1个结点，但是下标为0的置空不用，所以需要2n个结点，而m+1=2n；
    HT = (HuffmanTree)malloc(sizeof(HTNode) * m+1);          
    for (int i = 1; i <= m; i++)         //将2n-1个元素的lch，rch，parent置为0
    {
        HT[i].lch = 0;
        HT[i].rch = 0;
        HT[i].parent = 0;
    }
    for (int i = 1; i <= n; i++)
    {
        //输入前n个元素的weight值
        scanf("%d",&HT[i].weight);
    }
    //以上为初始化结束。
    
    //下面开始构造哈夫曼树
    //合并产生n-1个结点
    for (int i = n + 1; i <= m; i++)    //n+1是新产生结点的起始下标，m是新产生结点的结束下标
    {
        int s1 = 0;
        int s2 = 0;
        //在HT[k](1<=k<=i-1)中选择两个其双亲域为0，且权值最小的结点，并返回它们在HT中的序号s1，s2。
        Select(HT, i - 1, &s1, &s2);

        //表示从F中删除s1，s2
        HT[s1].parent = i;
        HT[s2].parent = i;

        //s1，s2分别作为i的左右孩子
        HT[i].lch = s1;
        HT[i].rch = s2;

        //i的权值为左右孩子权值之和
        HT[i].weight = HT[s1].weight + HT[s2].weight;
    }
}

int main()
{
    HuffmanTree HT = NULL;
    CreateHuffmanTree(HT, 3);
	return 0;
}

5、哈夫曼树应用

5.1、哈夫曼编码算法概念

5.1.1、哈夫曼编码思想

在远程通讯中，要将待传字符换成由二进制的字符串

设要传送的字符为：ABACCDA

若编码为：

A——00

B——01

C——10

D——11

所以传输字符ABACCDA就转换为传输为00010010101100，当对方接收到数据后，再根据相应的规则进行解码就行了。

这种叫做__定长编码方式。__

但是这种编码方式有个缺陷，就是，比较浪费空间。

但是若将编码设计为长度不等的二进制编码，即让代转字符串中__出现次数较多的字符采用尽可能短的编码__，则转码的二进制字符串便可能减少。

这种叫做__长度不等编码方式。__

就比如上面举的例子，要传输字符：ABACCDA。可以看到A，C是出现较多的字符，所以现将编码这样规定：

A——0

B——00

C——1

D——01

那ABACCDA就转换为000011010。

那我们来对比下：00010010101100（定长编码）和000011010（长度不等编码方式）的长度可以发现，确实后者可以减少空间浪费。

但是__长度不等编码方式__也有个缺陷，就是会造成重码的现象。

什么是重码呢？来解释下，就比如刚才我们使用长度不等编码方式将ABACCDA转为了000011010。我们来看000011010的前四位为是0，那前四个0组成的字符就会有多种情况：

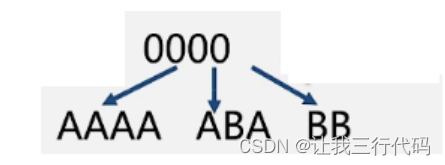
在这里插入图片描述

那到底代表那种字符呢？不知道，所以说这样就会造成错误。

为什么会造成重码呢？是因为一个字符是另一个字符的编码的前缀。比如：A代表0，B代表00，A就是B的编码的前缀。所以造成了重码！

那我们要如何设计长度不等编码呢？

可以这样：要设计长度不等的编码，则必须使任一字符的编码都不是另一个字符的编码的前缀。

这种编码称做：前缀编码。

那前缀编码怎么设计呢？就可以用哈夫曼编码进行设计。

所以当有问题：什么样的前缀编码能使得电文总长最短？答：哈夫曼编码。

5.1.2、如何实现哈夫曼编码

1、统计字符集中每个字符在电文中出现的平均概率（出现字符概率越大，要求编码越短）。

2、利用哈夫曼树的特点：权越大的叶子离根越近；__将每个字符的概率值作为权值，构造哈夫曼树。__则概率越大的结点，路径越短。

3、在哈夫曼树的每个分支上标上0或1：

结点的__左分支标为0，右分支标1；__

把从根到每个叶子的路径上的标号连接起来，作为该叶子代表的__字符的编码。__

看概念苦涩难懂，我们来看个案例：

要传输的字符集D={C,A,S,T,;}

字符出现频率	W={2,4,2,3,3}       //这里的频率就是哈夫曼树的权值

根据字符频率（权值）我们可以写出此哈夫曼树，并且所有的左子树标为1，右子树变为0。如下图：

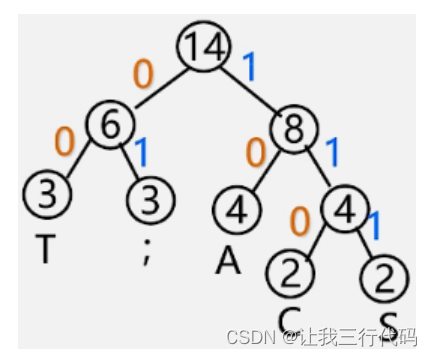
在这里插入图片描述

那我们从根节点出发到每一个叶子节点路过的所有分支的数字构成的数字符，我们就做为这个字符的字符编码。

如下字符集D的编码：

T——00
;——01
A——10
C——110
S——111

如上各字符的编码就叫做哈夫曼编码。

那好，既然学会了哈夫曼编码，那看个示例，写出此电文的哈夫曼编码{CAS;CAT;SAT;AT}。

那根据上面各字符的哈夫曼编码，我们可以写出此电文的哈夫曼编码：11010111011101000011111000011000。

反之，若编码是“1101000”，则其译文是：CAT。

5.1.3、哈夫曼编码的两个问题及两个性质

1、为什么哈夫曼编码能够保证是前缀编码？

答：

因为没有一片树叶是另一片树叶的祖先，所以每个叶节点的编码就不可能是其它叶节点编码的前缀。

如下图：

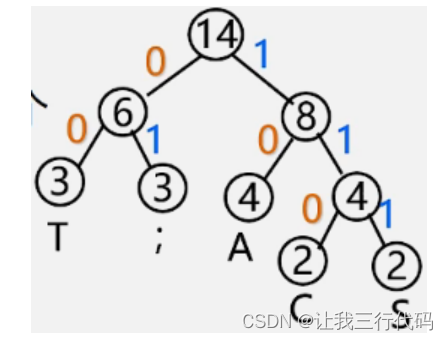
在这里插入图片描述

2、为什么哈夫曼编码能够保证字符编码总长最短？

答：

因为哈夫曼树的树带权路径长度最短，故字符编码的总长最短。

性质一：哈夫曼编码是前缀码。

性质二：哈夫曼编码是最优前缀码。

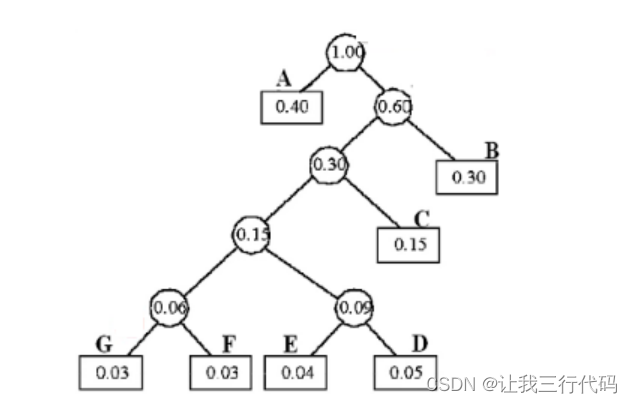
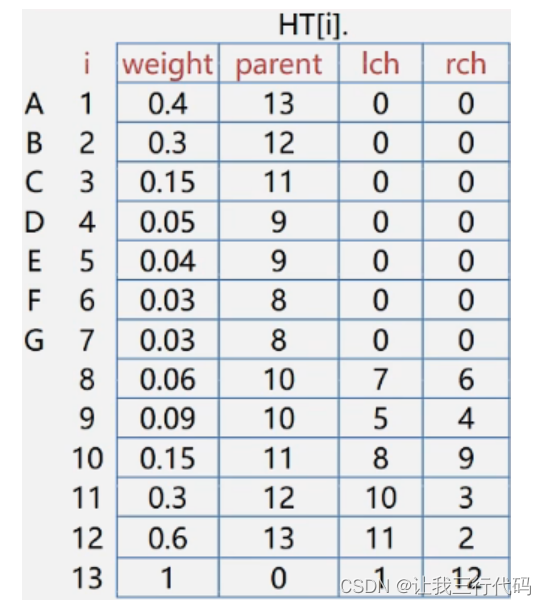
练习，设组成电文的字符集D及其概率分布W为：

D={A,B,C,D,E,F,G}

W={0.40,0.30,0.15,0.05,0.04,0.03,0.03}

请设计其哈夫曼编码。

这里直接写结果了：

首先得到哈夫曼树
并且此哈夫曼树抽象出来的逻辑关系，如下图：
将左分支标记为0，右分支标记为1，从而得到哈夫曼编码：

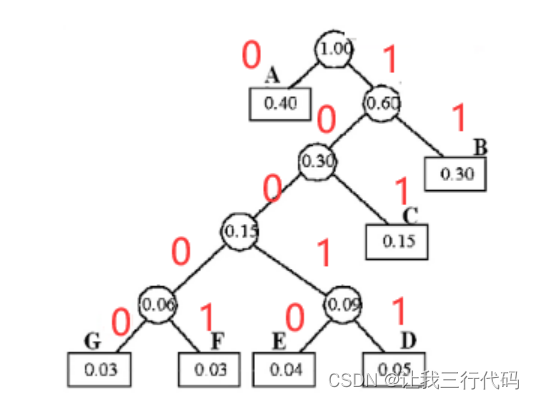
将从根节点到叶子结点路径上的数字符串联起来，就得到哈夫曼编码：

A——0
B——11
C——101
D——10011
E——10010
F——10001
G——10000

5.2、哈夫曼编码算法实现

5.2.1、过程分析

要想实现哈夫曼编码算法，前提必须先实现哈夫曼树算法。

哈夫曼算法抽象出来就是如下表格（使用上面一题的哈夫曼树表格）：

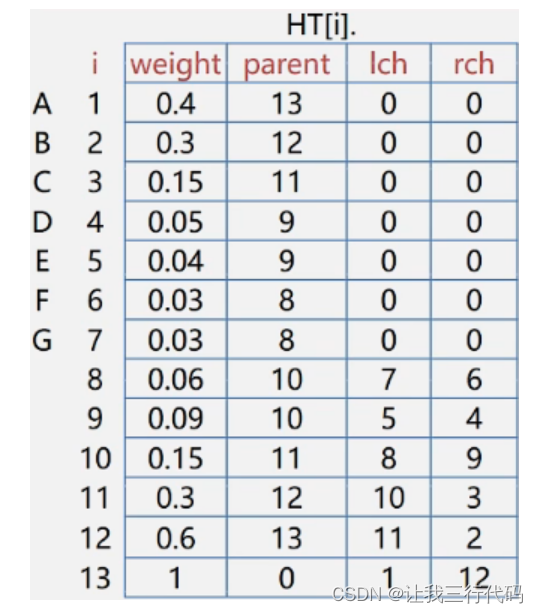
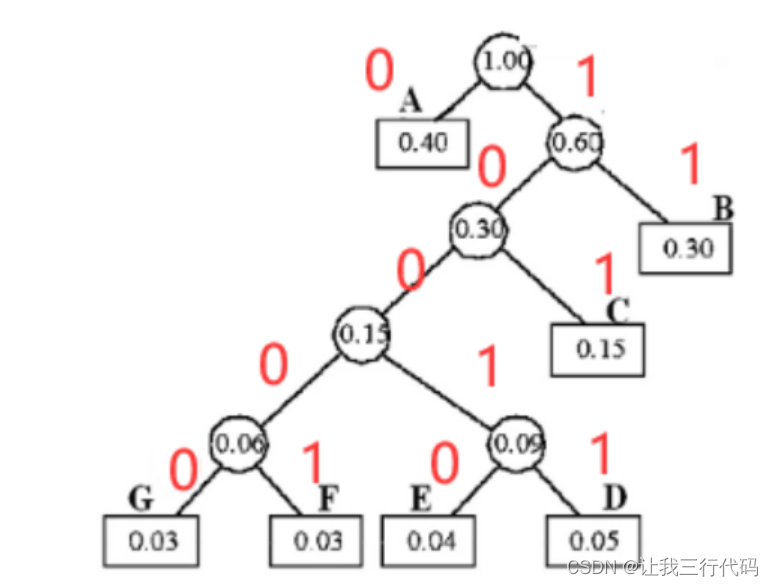
在这里插入图片描述

要想找到每个结点的哈夫曼编码，最主要的就是把从根节点到每个结点分支给标记出来：左分支标记为0，右分支标记为1。

想要实现如此算法，从__哈夫曼树尾部__开始是比较简单的。

下面我们就要找到：

G结点到根节点之间每个分支的数字字符（0|1），然后再将此数字字符串联起来即可。
F结点到根节点之间每个分支的数字字符（0|1），然后再将此数字字符串联起来即可。
E结点到根节点之间每个分支的数字字符（0|1），然后再将此数字字符串联起来即可。
D结点到根节点之间每个分支的数字字符（0|1），然后再将此数字字符串联起来即可。
…

这里演示一下——G结点到根节点之间每个分支是如何标记的。

过程如下：

（1）找到G结点，找到G结点中parent域值，这就相当于找到了G结点的双亲结点，然后再根据此双亲结点中的lch或者rch域，来匹配G结点的下标，如果lch匹配到了，说明G结点就是此双亲结点的左子树，那就将此左子树标记为0；如果rch匹配到了，说明G结点是此双亲结点的右子树，那就将此右子树标记为1。

接下来继续寻找

（2）现在只知道G结点和G结点的双亲结点的存储位置，而且G结点所在的分支已经标记过了，那现在就要标记G结点的双亲结点的分支（0.06这个结点），还是一样的步骤，先找0.06这个结点的partent域值，这就相当于找到了0.06结点的双亲结点，然后再根据此双亲结点中的lch或者rch域，来匹配0.06结点的下标，发现是左子树，所以做分支标记为0。

…

就这样一直查找、标记；查找、标记…

直到查找到根节点A，就会得到G结点的哈夫曼编码为：00001。

【注意】：这里我们找到G结点的哈夫曼编码是00001它和正确的哈夫曼编码正好相反。正确G结点的哈夫曼编码应该为：10000。为什么呢？起始原因很简单：因为我们是倒着从尾部的叶子节点G开始查找的。所以哈夫曼编码正好和正确的相反。