归并排序

算法流程：

1. 将数组A[1,n]排序问题分解为A[1,n/2]和A[n/2+1,n]排序问题
2. 递归解决子问题得到两个有序的子数组
3. 将两个子数组合并为一个有序数组

符合分而治之的思想：

1. 分解原问题
2. 解决子问题
3. 合并问题解

递归式求解

递归树法

用树的形式表示抽象递归

$T(n)=\{\begin{array}{llc}2T(\frac{n}{2})+O(n),& if& n>1\\ O(1),& if& n=1\end{array}$

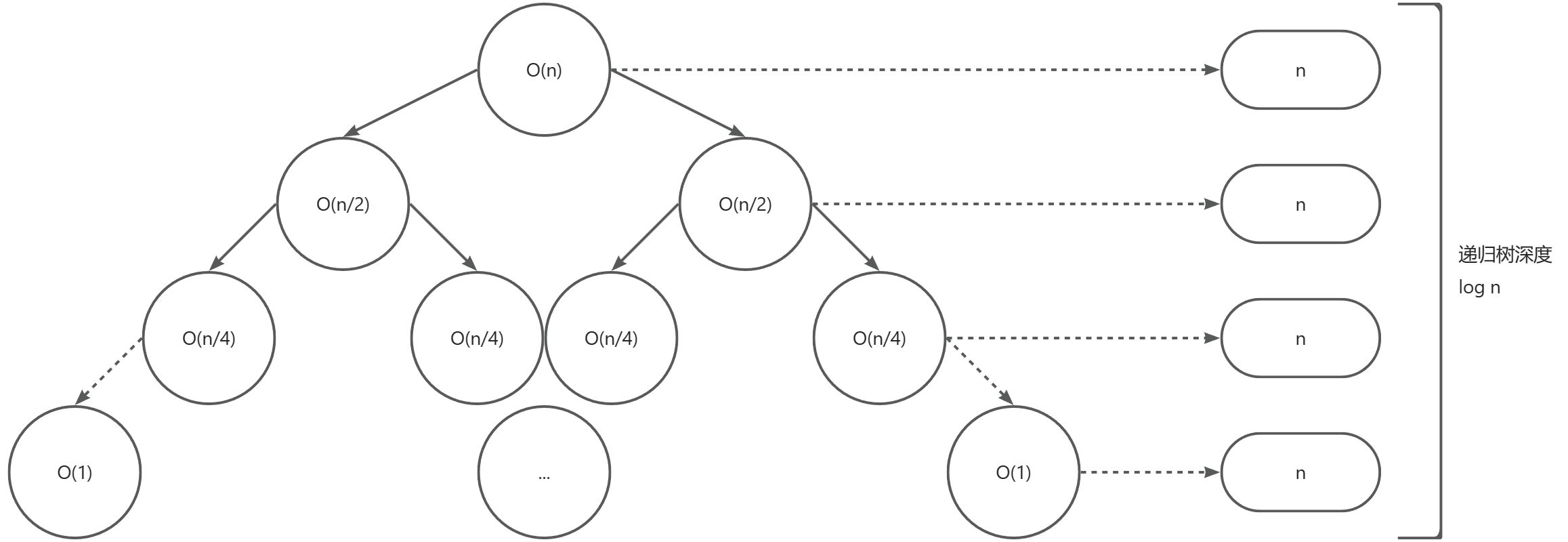
树的深度通常从0开始计，故层数等于n+1，后续统一用深度
可以得到，这个算法的时间复杂度是：$T(n)=O(n\log n)$

主定理法

对形如$T(n)=aT(\frac{n}{b})+f(n)$的递归式：

• 每个节点共a个分支
• 每层以因子b速度下降
• $n^{{\log }_{b}a}$代表每层叶子节点代价之和

可以得到如下公式：
KaTeX parse error: {align} can be used only in display mode.
当$f(n)$形式为$n^k$时，可简化主定理公式：
KaTeX parse error: {align} can be used only in display mode.
例：$T(n)=5T(\frac{n}{2})+n^3$

1. $k=3$
2. $a=5,b=2,{\log }_{b}a={\log }_{2}5$
3. $k>{\log }_{b}a$
4. $T(n)=\Theta (n^3)$

最大子数组

基于枚举策略

蛮力枚举：枚举所有可能的情况
枚举$n+C_n^2$种可能的区间$[l,r],(l<r)$，求解最大子数组之和$S_{max}$，时间复杂度为$O(n^3)$。
优化枚举：蛮力枚举存在重复计算
$S(l,r)={\Sigma }_{i=1}^{r}X[i]=S(l,r-1)+X[r]$，时间复杂度为$O(n^2)$

分而治之

1. 将数组$X[\mathrm{1..}n]$分为$X[\mathrm{1..}n/2]$和$X[n/2+\mathrm{1..}n]$
2. 递归求解子问题：
   1. $S_1$：数组$X[\mathrm{1..}n/2]$的最大子数组
   2. $S_2$：数组$X[n/2+\mathrm{1..}n]$的最大子数组
3. 合并子问题，得到$S_{max}$
   1. $S_3$：跨中点的最大子数组
   2. 数组$X$的最大子数组之和 S m a x = m a x { S 1 , S 2 , S 3 } S_{max}=max\{S_1,S_2,S_3\} Smax​=max{S1​,S2​,S3​}

问题在于，如何高效地求解$S_3$

1. 记$mid=\frac{n}{2}$
2. $S_3$可以分为左右两部分：
   1. $Left$：以$X[mid]$为结尾的最大子数组之和
   2. $Right$：以$X[mid+1]$为开头的最大子数组之和
   3. $S_3=Left+Right$

求解$S_3$的时间复杂度分析：

1. 求解$Left$：从$X[mid]$向前遍历求和，并记录最大值，时间复杂度为$O(mid)$
2. 求解$Right$：从$X[mid+1]$向后遍历求和，并记录最大值，时间复杂度为$O(n-mid)$
3. 求解$S_3$的时间复杂度：$O(n)$

伪代码：

输入：数组X，数组下标low，high
输出：最大子数组之和Smax
if low=high then
|	return X[low]
end
else
|	mid	<-	(low+high)/2
|	S1	<-	MaxSubArray(X,low,mid)
|	S2	<-	MaxSubArray(X,mid+1,high)
|	S3	<-	CrossingSubArray(X,low,mid,high)
|	Smax	<-	Max(S1,S2,S3)
|	return Smax
end

时间复杂度分析

$T(n)=
\left{
\begin{align}
&1,\quad&n=1\
&2T(\frac n2)+O(n),\quad&n>1
\end{align}
\right.
\$
按照上面提到的递归树求解的方法，可以得到：$T(n)=n\log n$

逆序对计数

逆序对：当$i<j$时$A[i]>A[j]$的二元组$(A[i],A[j])$。

蛮力枚举

对于数组的每个元素$A[i]$，枚举$j(j>i)$，并统计逆序对数目。
伪代码：

输入：一个大小为n的数组A[1..n]
输出：数组A[1..n]中逆序对数目Sum
Sum	<-	0
for i <- 1 to n do
|	for j <- i+1 to n do
|	 |	if A[i]>A[j] then
|	 |	|	Sum <- Sum+1
|	 |	end
|	end
end
return Sum

这一算法时间复杂度为$O(n^2)$

分而治之

1. 将数组$A[\mathrm{1..}n]$分为$A[\mathrm{1..}\frac{n}{2}]$和$A[\frac{n}{2}+\mathrm{1..}n]$
2. 递归求解子问题
   1. $S_1$：仅在$A[\mathrm{1..}\frac{n}{2}]$中的逆序对数目
   2. $S_2$：仅在$A[\frac{n}{2}+\mathrm{1..}n]$中的逆序对数目
3. 合并$A[\mathrm{1..}n]$分为$A[\mathrm{1..}\frac{n}{2}]$和$A[\frac{n}{2}+\mathrm{1..}n]$的解
   1. $S_3$：跨越子数组的逆序对数目
   2. $S=S_1+S_2+S_3$

策略一：直接求解

对每个$A[j]\in A[m+1,n]$，枚举$A[i]\in A[\mathrm{1..}m]$并统计逆序对数目。
求解$S_3$的算法运行时间：$O(n^2)$
分而治之框架的运行时间：$T(n)=2T(\frac{n}{2})+O(n^2)$
直接求解的分而治之较蛮力枚举并未提高算法运行时间。

• 运行时间受制于跨越子数组的逆序对计数方法
• 数组的有序性通常有助于提高算法的运行时间

策略二：排序求解

1. 分别对数组$A[\mathrm{1..}m]$和$A[m+\mathrm{1..}n]$进行排序
2. 对于每个$A[j]\in A[m+\mathrm{1..}n]$，采用二分查找为其在$A[\mathrm{1..}m]$中定位
3. $A[j]$在$A[\mathrm{1..}m]$定位点右侧的元素均可与$A[j]$构成逆序对

求解$S_3$的算法运行时间：$O(n{\log }^{2}n)$
分治框架的算法运行时间：$T(n)=2T(\frac{n}{2})+O(n\log n)$

算法优化

合并问题解的同时对数组进行排序

• 归并过程中可同时计算逆序对数目

策略三：归并求解

1. 从左到右扫描有序子数组：$A[i]\in A[\mathrm{1..}m],A[j]\in A[m+\mathrm{1..}n]$
   1. 如果$A[i]>A[j]$，统计逆序对，$j$向右移
   2. 如果$A[i]<A[j]$，$i$向右移
2. 利用归并排序框架保证合并后数组的有序性

伪代码：

输入：数组A[1..n]，数组下标left,right
输出：数组A[left..right]的逆序对数，递增数组A[left..right]
if left >= right then
|	return A[left..right]
end
mid	<-(left+right)/2
S1	<- CountInver(A,left,mid)
S2	<- CountInver(A,mid+1,right)
S3	<- MergeCount(A,left,mid,right)
S		<- S1+S2+S3
return S,A[left..right]

时间复杂度：$T(n)=O(n\log n)$

快速排序

归并排序：简化分解，侧重合并
快速排序：侧重分解，简化合并

数组划分

1. 任选$x$作为分界线，称为主元
2. 交换重排，满足$x$左侧元素小于右侧

实现方法：

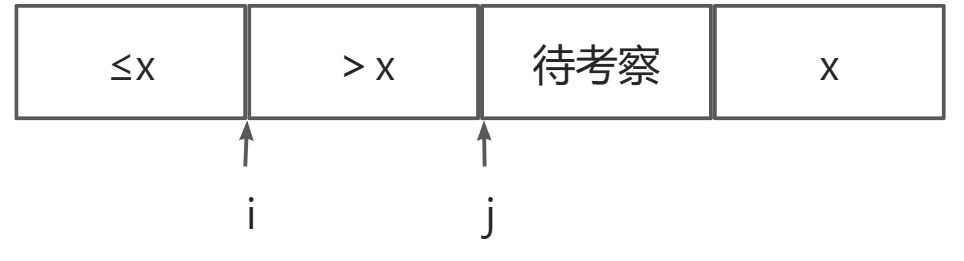
1. 选取固定位置主元$x$，如尾元素
2. 维护两个指针变量，分别指向两个部分的右端点
3. 考察数组元素$A[j]$，只和主元比较
   1. 若$A[j]\le x$，则交换$A[j]$和$A[i]+1$，$i$与$j$右移
   2. 若$A[j]>x$，则$j$右移
4. 把主元放在中间作分界线

伪代码Partition(A,p,r)

输入：数组A，起始位置p，终止位置r
输出：划分位置q
x <- A[r]//选取主元
i <- p-1
for j <- p to r-1 do
 | if A[j] <= x then
 | | exchange A[i+1] with A[j]
 | | i <- i+1
 | end
end
exchange A[i+1] with A[r]
q <- i+1
return q

快速排序的伪代码

输入：数组A，起始位置p，终止位置r
输出：有序数组A
if p<r then
| q <- Partition(A,p,r)
| QuickSort(A,p,q-1)
| QuickSort(A,q+1,r)
end

最好情况：$O(n\log n)$
最坏情况：$O(n^2)$
快速排序看似不优于归并排序。

次序选择问题

输入：

• 包含$n$个不同元素的数组$A[\mathrm{1..}n]$
• 整数$k$

输出：

• 数组$A[\mathrm{1..}n]$中第$k$小的元素$(1\le k\le n)$

固定位置划分求解

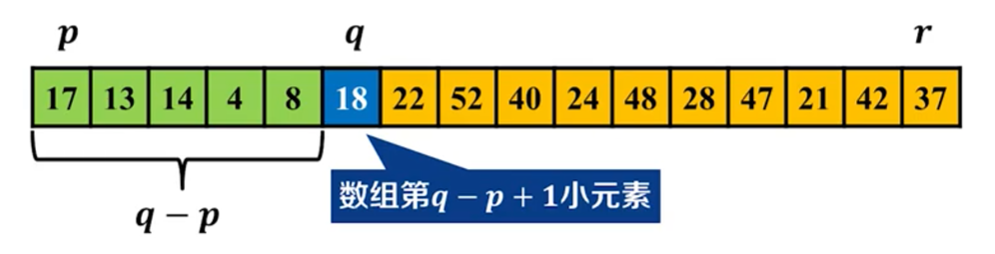
选取固定位置主元，小于主元的元素个数$q-p$：

• 情况1：$k=q-p+1$，$A[q]$为数组第$k$小元素
• 情况2：$k<q-p+1$，在$A[p..q-1]$中寻找第$k$小元素
• 情况3：$k>q-p+1$，在$A[q+\mathrm{1..}r]$中寻找第$k-(q-p+1)$小元素

子问题始终唯一，无需合并问题解。

伪代码

输入：数组A，起始位置p，终止位置r，元素次序k
输出：第k小元素x
q <- Partition(A,p,r)
if k=(q-p+1) then
| x <- A[q]
end
if k<(q-p+1) then
| x <-Selection(A,p,q-1,k)
end
if k>(q-p+1) then
| x <- Selection(A,q+1,r,k-(q-p+1))
end
return x

复杂度分析：
最好情况：$T(n)=\Omega (n)$
期望时间复杂度：$T(n)=\Theta (n)$
最坏情况：$T(n)=O(n^2)$