正值国庆之际,祝愿祖国繁荣昌盛,祝愿朋友一生平安!终身学习,奋斗不息!
目录
1.贪心算法简介
2.贪心算法的特点
3.如何学习贪心算法
题目练习(持续更新)
1.柠檬水找零(easy)
算法原理
代码实现
证明(交换论证法)
1.贪心算法简介
贪心策略:解决问题的一种策略,由局部最优->全局最优。
一般步骤:
1.把解决问题的过程分为若干步
2.解决每一步的时候,都选择当前“最优的”解法
3.“希望”得到全局最优解
例1:找零问题
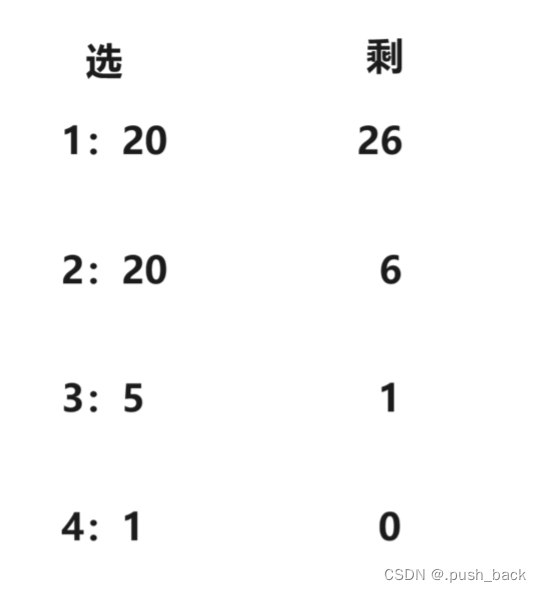
有20,10,5,1面值货币若干张,如何用最少的张数支付46元?
贪心策略:每次选取尽可能大的货币
例2:背包问题
一个背包容量为8,有3种物品若干,选择要装的物品,使背包内物品总价值最大
贪心策略:每次选择单位体积价值尽可能大的物品。类似也可选择体积小(装更多的物品,总价值可能最大),价值大(每次选价值大的,总价值可能最大)。
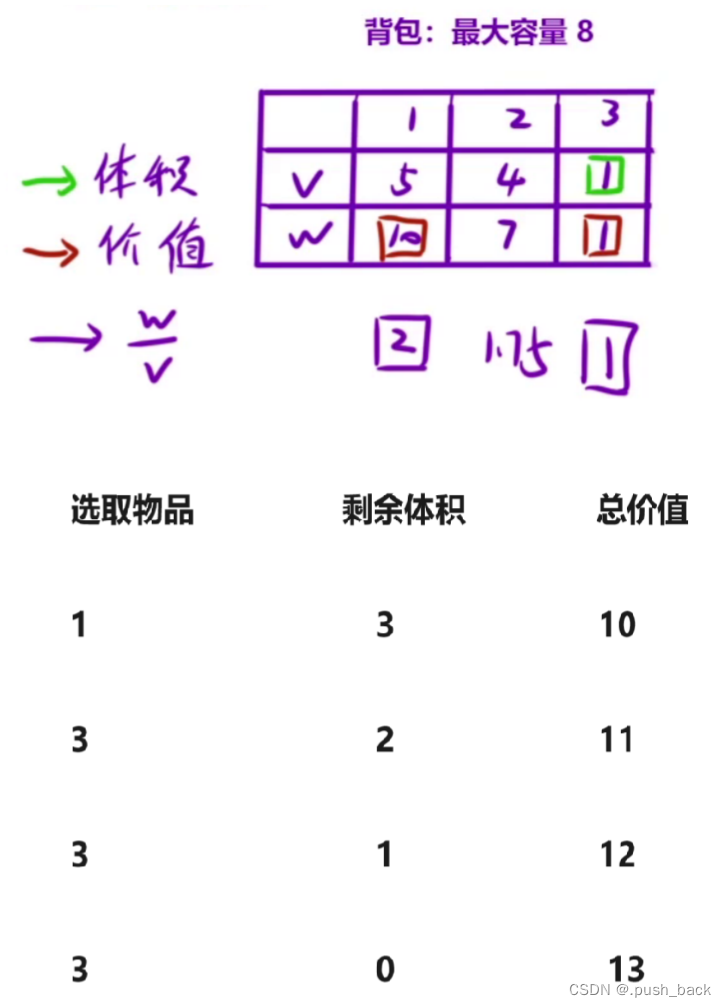
通过贪心策略得到的结果是13,这并不是最优解(选取2个物品2,总价值14),所以贪心策略考虑的是局部最优,全局不一定最优。
2.贪心算法的特点
1.贪心策略没有标准,不同的问题选取的标准不同
2.贪心不一定得到全局最优解,正确的贪心策略需要被“证明”
证明方法:所有可用的数学证明方法
证明:找零问题的贪心策略
在例1中使用的贪心策略是每次选取尽可能大的货币,接下来证明它的正确性,即该贪心策略能够得出最优解。
分析最优情况下的性质:
设不同面值货币使用张数分别为A,B,C,D
B有三种可能:B>2;B=2;B<2
当B>=2时,每两张10元货币都可以用一张20元货币代替,所以要使总货币张数最少,B只能<2。同理,C<2;D<5
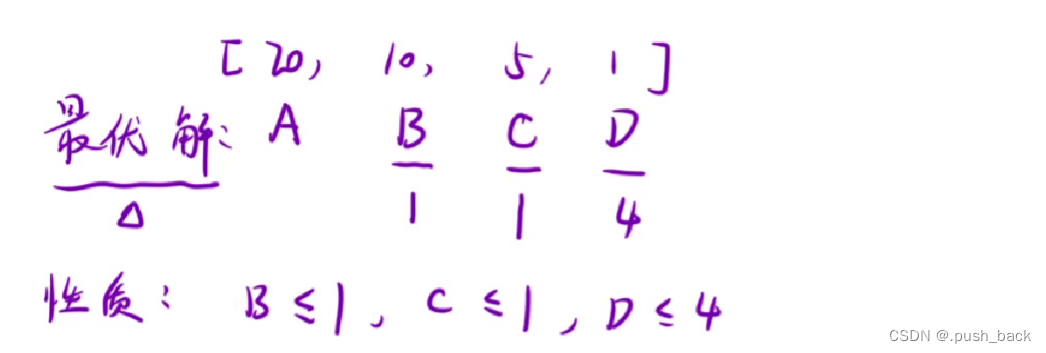
设贪心策略下不同面值货币使用张数分别为a,b,c,d
现在只需证明a=A,b=B,c=C,d=D即可
根据贪心策略,显然a>=A。如果a>A,那么相差的每个20元,需要其它面值货币凑够,根据性质,B,C,D最大得到的总额是10+5+4=19元<20元,需要增加货币张数,不符合性质。所以a=A。
同理可证,b=B,c=C,d=D
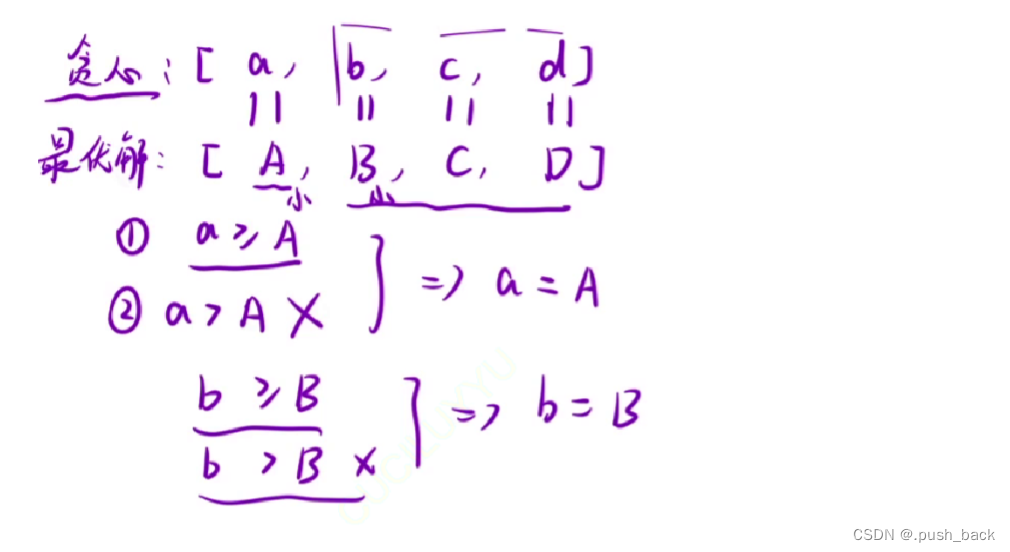
综上,该贪心策略得到的就是最优解。
3.如何学习贪心算法
1放平心态
贪心算法并不是一种模版,它是一种解题策略。对于一些题目,想不到正确的贪心策略很正常。
2积累经验
学习贪心算法时,应该把重点放在贪心的策略上,对于每一道题目的贪心策略,我们应该当成经验去吸收,积累多了,我们“贪心的思维”自然就熟练了。
3尝试证明
一些贪心题目的原理比较简单,理解了贪心算法后基本不需要证明,对于一些较难的题目,我们学会解决它的贪心策略后可以尝试理解或证明它的正确性。
题目练习(持续更新)
1.柠檬水找零(easy)
题目链接:柠檬水找零
题目描述:


算法原理
1讨论找零情况:
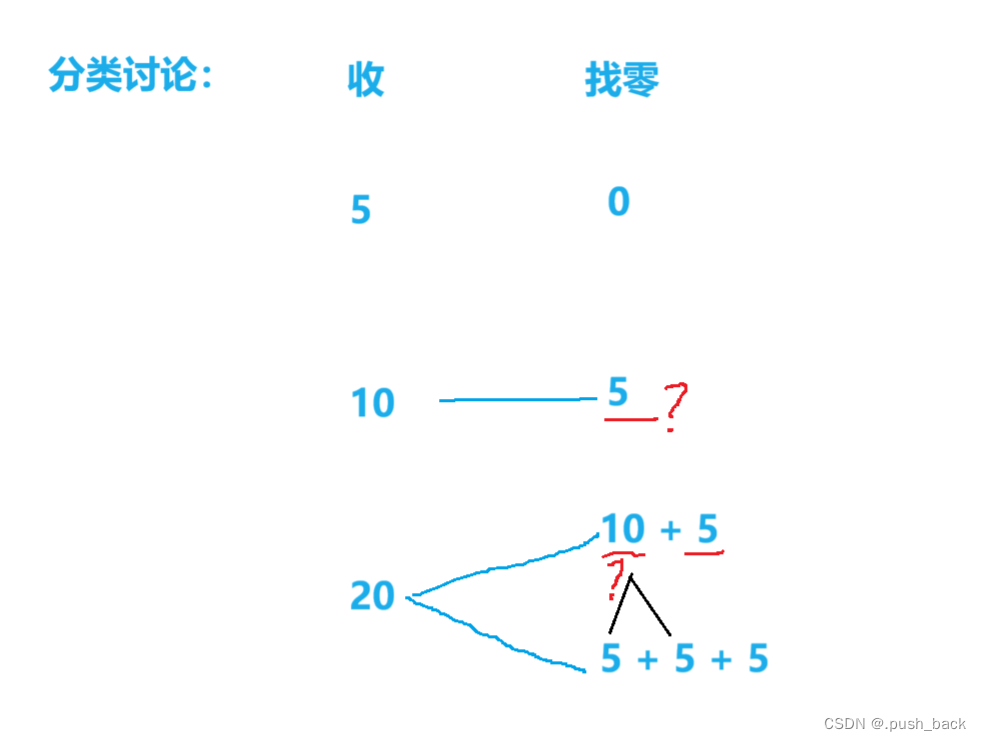
2贪心策略
给20元找零有两种方式,需要选择最优的方式(完成更多的交易)
示例:已有5,5,5,10,下面的支付金额顺序是20,10
选择10+5方式找零,还剩5,5,可以用一个5给下一个10找零,true
选择5+5+5方式找零,给20找完后无剩余5,不能给下一个10找零,false
5元既可以给10元找零也可以给20元找零,所以本题的贪心策略是保留更多的5元,即给20找零优先使用10+5。
代码实现
用两个变量分别统计收下5,10的个数
找零(按分类讨论和贪心实现),5,10对应变量减去数量即可
无法找零返回false
C:
bool lemonadeChange(int* bills, int billsSize){
int five = 0, ten = 0;
for (int i = 0; i < billsSize; i++)
{
// 分类讨论
if (bills[i] == 5)
five++;
else if (bills[i] == 10)
{
if (five == 0)
return false;
five--;
ten++;
}
else
{
if (ten && five)// 贪心
{
ten--;
five--;
}
else if (five >= 3)
{
five -= 3;
}
else
return false;
}
}
return true;
}C++:
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int five = 0, ten = 0;
for (auto x : bills)
{
// 分类讨论
if (x == 5)
five++;
else if (x == 10)
{
if (five == 0)
return false;
five--;
ten++;
}
else
{
if (ten && five)// 贪心
{
ten--;
five--;
}
else if (five >= 3)
{
five -= 3;
}
else
return false;
}
}
return true;
}
};证明(交换论证法)
交换论证法:假设一种接近贪心算法的最优算法,通过交换它的一个步骤或元素,该算法的最优性不变,或者更接近贪心算法(贪心算法更优),那么贪心算法就是最优解。
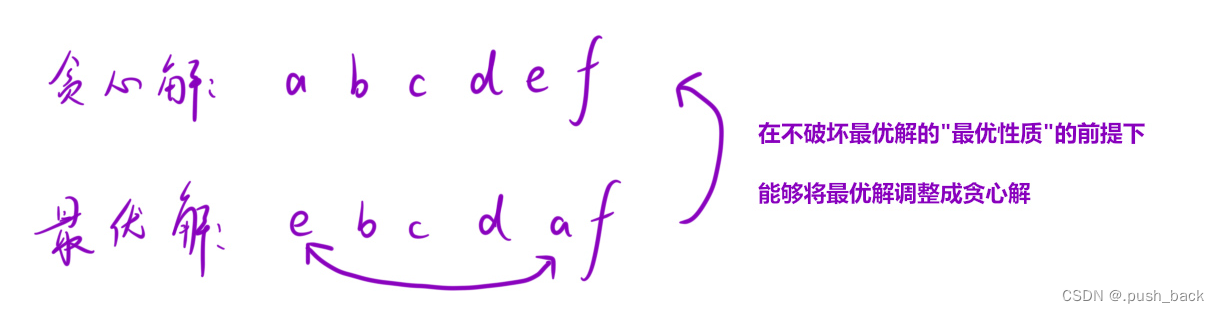
证明该题目贪心策略的最优性:
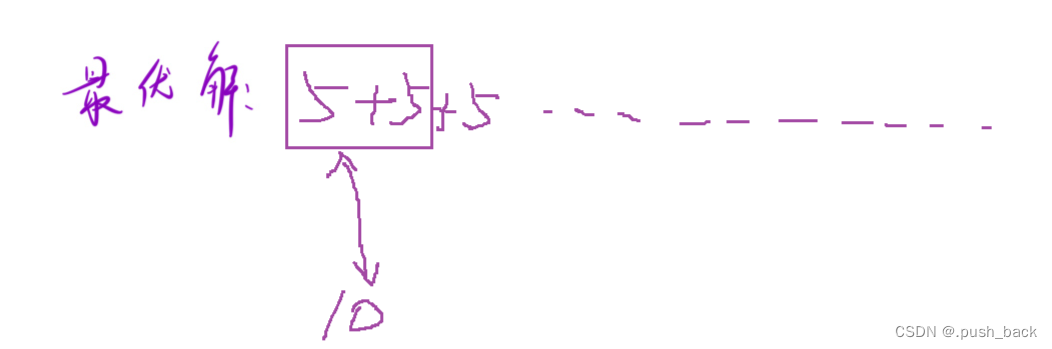
假设最优解其中一步给20找零使用5+5+5
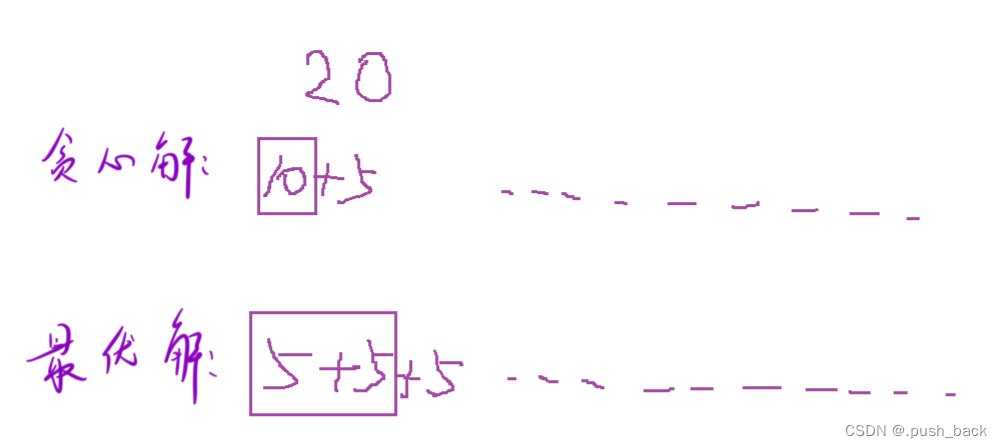 讨论:
讨论:
①最优解后面没有用贪心解的那个10找零
用10交换最优解给20找零的其中2个5,其仍然是最优解
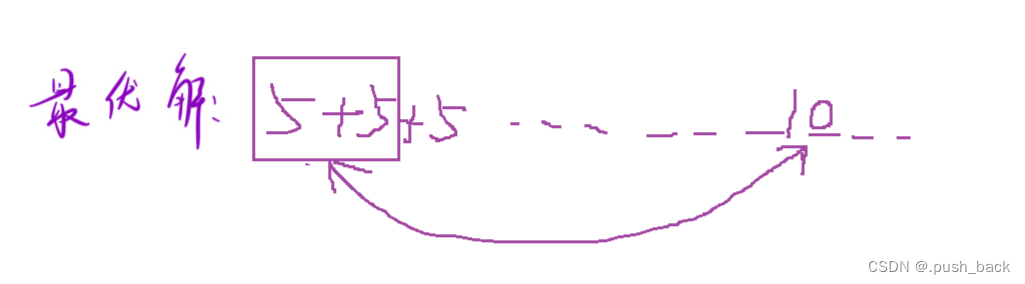
②最优解后面有一次用了贪心解的10找零
给20找零的其中两个5可以与后面使用的10交换,其仍然最优
综上,该贪心算法是最优解(正确解)

其它贪心题目会根据个人学习情况不定时更新,敬请期待。
如果本文内容对你有帮助,可以点赞收藏,感谢支持,期待你的关注。








![[React] Zustand状态管理库](https://img-blog.csdnimg.cn/199d8d74875d4e598f33a97e0c20312d.png)