2022 ICDE
1 intro
1.1 背景
轨迹相似度可以划分为:
- 非学习度量方法
- 通常是为一两个特定的轨迹距离度量设计的,因此不能与其他度量一起使用
- 通常需要二次时间(O(n^2))来计算轨迹之间的精确距离
- 基于学习的度量方法
- 利用机器学习技术学习轨迹的适当表示,用于任何一种距离度量
- 在预处理阶段(训练阶段?)之后,数据库中的每条轨迹都被转换成d维空间中的一个向量
- 然后,两条轨迹之间的相似性可以通过两个相应向量之间的距离(例如,欧几里得距离)来近似,这只需要O(d)时间
- 通过这样做,计算轨迹之间的相似性变得高度时间有效
- 比DTW快了大约6个数量级
1.2 现有基于学习的方法的瓶颈
- 基于学习的模型将轨迹嵌入为多维点,这些模型计算距离的效率没有区别
- 几乎所有现有的基于学习的方法都是基于递归神经网络(RNNs)设计的
- 在这个框架下,每个轨迹的表示几乎都是在训练过程中独立于其他轨迹学习的
- ——>侧重于每个单独轨迹的内部信息,但忽略了轨迹之间的信息,即轨迹之间的相互作用/相关性
- 这些相互作用/相关性指的是轨迹之间的信息,具体来说,是点匹配信息
- 在这个框架下,每个轨迹的表示几乎都是在训练过程中独立于其他轨迹学习的

- 红线和灰线都表示轨迹之间的点匹配
- 在相似性计算过程中轨迹之间的顶点对应关系
- 轨迹之间缺乏相关性导致了这些基于学习的模型在近似精度方面的性能有限
1.3 motivation
- 传统轨迹距离度量首先找到两个轨迹之间的点的匹配,然后累积这些匹配对的信息以获得轨迹相似性分数
- 如上图的DTW,轨迹距离计算严重依赖于一对轨迹之间的点匹配过程
- 基于学习的方法都忽略了这个重要的信息,即轨迹之间的点的映射
- ——>这些模型不能在训练过程中适应地捕捉两个轨迹之间用于相似性计算的相关性,从而限制了近似精度
- ——>论文使用attention机制,在计算轨迹相似性时捕捉到每个点的匹配点
- 之前使用attention的轨迹相似度方法主要用于一个轨迹内的点,不能正确捕捉轨迹之间的相关性
1.4 论文方法
- 论文提出了一种名为TMN的新型基于匹配的模型,用于学习近似轨迹相似性
-
Trajectory Matching Networks
-
利用一种匹配机制,其目标是将一条轨迹中的点匹配到另一条轨迹中的点
-
匹配机制本质上依赖于注意机制,它能够计算点之间的相似性,以便点可以跨轨迹匹配
-
然后将匹配信息与轨迹的空间信息结合起来,并送到一个RNN,用RNN来学习轨迹表征
-
2 related work
这里就说一点吧,论文提到了GTS框架,其目标是解决空间网络(道路网络)上的轨迹相似性学习问题。
论文的方法是不涉及网络结构(GTS:graph中的一系列节点,本文:轨迹的坐标元组)
本文使用非GTS框架进行实验
3 Preliminary
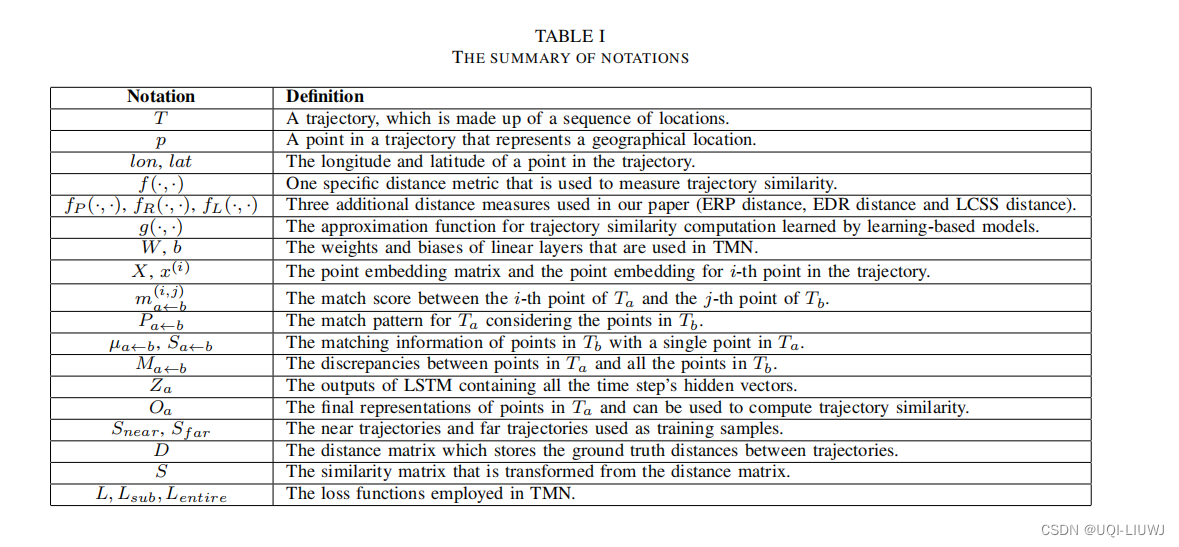 3.1 轨迹
3.1 轨迹
按时间戳 t 排序的样本点序列。
每个样本点 p 都是二维空间中的一个位置
轨迹 T 由一系列样本点表示,T=(p(1),p(2),…,p(n))
通常,点p(i) 被表示为经度=lon(i) 和纬度=lat(i)。
3.2 轨迹相似性学习
给定一个特定的轨迹相似性度量f(⋅,⋅) 和一对轨迹Ti,Tj,轨迹相似性学习旨在学习一个近似相似性函数g(Ti,Tj) 以最小化∣∣f(Ti,Tj)−g(Ti,Tj)∣∣
3.3 距离度量
- 已经提出了相当多的轨迹距离度量来测量轨迹之间的(不)相似性
- 不同的距离度量强调轨迹中包含的不同信息
- 论文主要使用ERP、EDR和LCSS
H(Ti) 是Ti 中的第一个点(头)
R(Ti) 代表包含 Ti 中除第一个点之外的其余点的子轨迹
4 方法
4.1 方法

4.2 采样方法
- 在训练过程中需要向TMN提供轨迹对
- 对训练集中的每条轨迹采样两种类型的轨迹:一种是靠近锚轨迹的轨迹,另一种是远离锚轨迹的轨迹
- Traj2SimVec将轨迹均匀压缩成相同数量的段,然后构建一个k-d树来存储简化的轨迹
- 在k-d树的帮助下,Traj2SimVec从k-d树中锚轨迹的k个最近邻中选择近样本
- 然而,这种方法可能会遇到以下缺点
- Traj2SimVec的采样方法在所有距离度量下保持不变,因此它可能无法很好地捕获每个距离度量的相似性信息
- 由于近样本总是从k个最近邻中选取的,其中k在Traj2SimVec中设定为5,该模型只能选择这些数据作为近样本,并忽略k-d树中的所有其他点
- ——>论文提出了一种不同的采样方法
- 对于一个锚轨迹Tanc,论文从训练集中随机选择2k个样本
- 然后,我们根据这些样本离Tanc的距离对它们进行排序,并将排序后的样本记录在一个列表中(T1,T2,…,T2k)
- 使用前k个轨迹形成近训练对,最后k个轨迹作为远训练样本
- ——>这种策略确保在每个小批量中,近样本总是比远样本更接近锚轨迹
- ——>与Traj2SimVec相比,可以使用这种方法采样更多的轨迹作为近训练样本,而且不同的轨迹相似性度量下训练样本会有所不同
4.3 训练目标
- 给定一个特定的距离度量,预计算距离矩阵D以供训练和测试使用
- 在训练期间,
被用来提供训练对之间的距离,其中 tn 代表训练集中的轨迹数量。
- 由于轨迹距离度量衡量的是轨迹之间的距离而不是相似性,距离矩阵D被转换为相似性矩阵 S∈Rn×n (这里个人觉得n就是tn?)
- S=exp(−α⋅D),其中Si,j∈(0,1) 被用作Ti和Tj之间的相似性
- 在训练期间,
- 近似轨迹相似性本质上是一个回归问题,因此论文使用均方误差(MSE)作为损失函数
- 损失函数由两部分组成
- 第一部分,全局角度
- 轨迹对的基本真实相似性与预测相似性之间的差异
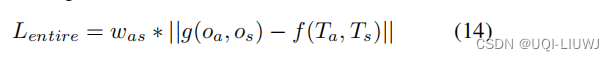
- Ta是锚轨迹,Ts是采样轨迹
- Oa,Os是对应的表征
- Was是一个权重,和Ta越相似的采样轨迹,Was越大
- 假设我们为一个锚轨迹抽样 n 个轨迹作为近样本,然后我们根据它们与锚轨迹的相似性按降序排列这些样本,并得到一个样本列表

- 进一步地,这些排名的样本使用以下列表被分配权重,
- 假设我们为一个锚轨迹抽样 n 个轨迹作为近样本,然后我们根据它们与锚轨迹的相似性按降序排列这些样本,并得到一个样本列表
- ——>最接近锚轨迹的轨迹被分配最大的权重,以便 TMN 主要受到更近的轨迹的影响
- 第二部分:子轨迹角度
- 每条轨迹都包含许多子轨迹,这些子轨迹之间的距离可以在训练期间预先计算出来
- 这些额外的训练数据有助于提高 TMN 的学习能力
- 训练集中的轨迹被划分为几个子轨迹,计算出每一对子轨迹之间的距离。然后,计算子轨迹损失

表示包含了前i个点的Ta,
表示对应的向量
- r是在训练期间使用的子轨迹对的数量
- 在 TMN 中,通过将第一个点作为起点,每10个点作为一个新的终点来抽取子轨迹。
- 例如,给定长度为 53 的轨迹 Ta,抽取五个子轨迹Ta[1:10],..., Ta[1:50]
- 第一部分,全局角度
- ——>总体损失函数
5 实验
5.1 数据集
- Geolife由北京的182个用户收集,它包含了一系列广泛的人类户外运动,这些运动是用户的GPS位置。总共,Geolife中有17,612条轨迹。
- Porto包含超过170万辆车辆路线轨迹,主要由葡萄牙波尔图的442辆出租车收集。
- 遵循以前的工作,过滤掉位于稀疏区域的轨迹,保留位于城市中心区域的轨迹进行训练和测试。
- 还移除了少于10条记录的轨迹。
- 这是因为计算较长序列的相似性更困难且耗时。
- 因此,这些较长的计算时间更明显地显示了模型之间的差异。
- 此外,轨迹数据集通常以许多GPS错误和其他问题为特征,受影响的短轨迹严重受到这些错误的影响。
- 这是因为计算较长序列的相似性更困难且耗时。
- 经过预处理后,Geolife数据集中大约有8,000条轨迹,Porto数据集中有600,000条轨迹。
5.2 评估标准
在实验中采用了Hausdorff、Fréchet、DTW、ERP、EDR、LCSS距离度量。
- 遵循之前的工作,进行轨迹相似性搜索,以评估不同模型在两个数据集上的性能。
- 采用HR-10、HR-50和R10@50作为主要的评估指标。
- HR-k是前k个命中比率,它检查由学到的前k个结果恢复的基准真实轨迹的重叠百分比,即前k个结果和基准真实值的重叠百分比。
- Rk@t是对前k个基准真实值的前t个召回,它评估了由不同方法产生的前t个中恢复的前k个基准真实值。更高的召回值表示性能更好。
- 采用HR-10、HR-50和R10@50作为主要的评估指标。
5.3 实验结果
5.3.1 效果
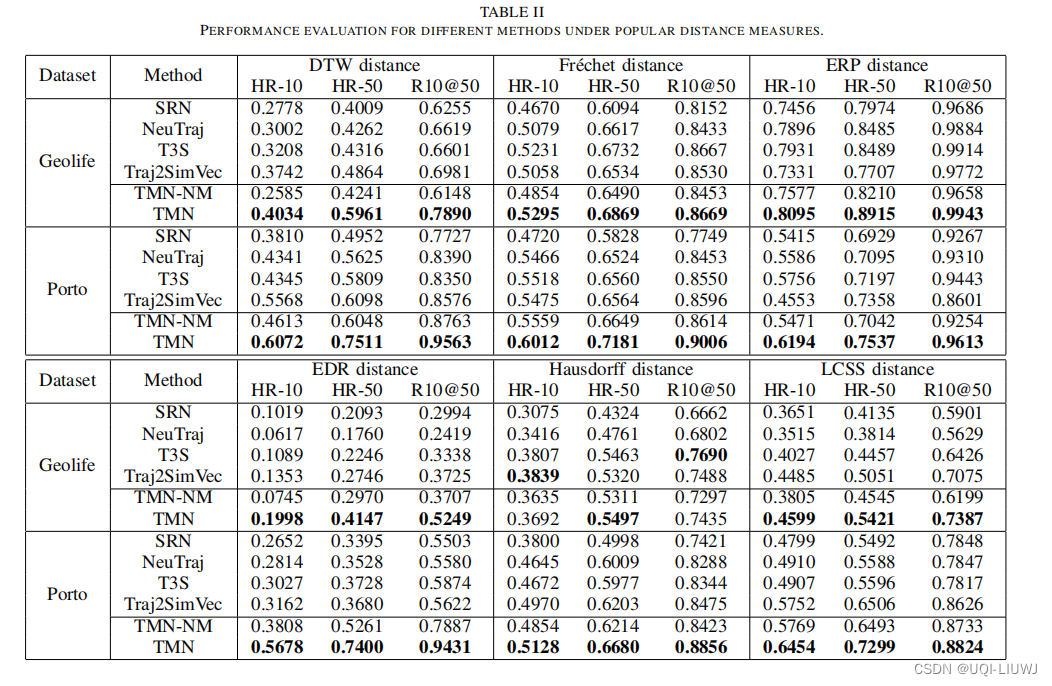
5.3.2 有效性
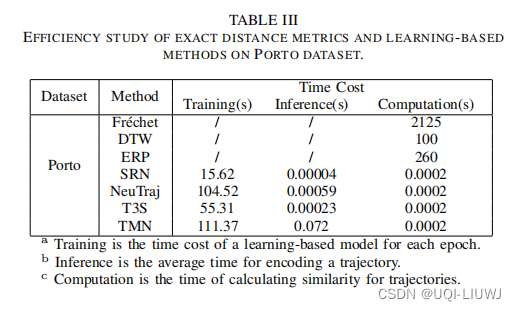
5.3.3 不同采样效果(使用or不使用KD树)

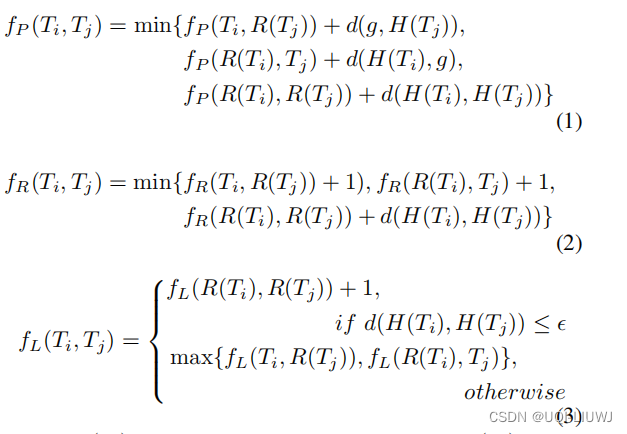
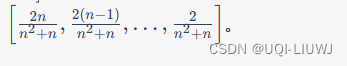








![[React] Zustand状态管理库](https://img-blog.csdnimg.cn/199d8d74875d4e598f33a97e0c20312d.png)