目录
一、动态数组
1、创建动态数组
2、添加元素
3、删除修改元素
4、访问元素
5、返回数组长度
6、for each遍历数组
二、输入多个数字
1、正则表达式
2、has.next()方法
三、矩阵连乘
1、什么是矩阵连乘?
2、动态规划思路
3、手推m和s矩阵
4、完整代码
5、备忘录方法
四、凸多边形剖分
1、凸多边形形三角剖分原理
2、完整代码
一、动态数组
1、创建动态数组
创建动态数组ArrayList,先调用ArrayList库,之后动态创建语句如下,括号内填写数组元素个数,不知道可以不填。
import java.util.ArrayList;
ArrayList<Integer> num = new ArrayList<>();2、添加元素
使用函数add添加元素。如:添加元素1。
num.add(1);如果创建一个ArrayList num与list1相同(num和list1同为ArrayList类型)
ArrayList<Integer> num = new ArrayList<>(list1);3、删除修改元素
使用函数remove删除特定索引的元素。如:删除索引为1的元素。
num.remove(1);使用函数set修改特定索引的元素。如:将索引为1的元素修改为"java"。
num.set(1,"java");4、访问元素
使用函数get返回特定索引的元素。如:返回索引1的元素并打印。
system.out.println(num.get(1));5、返回数组长度
使用函数size()返回数组长度。如:返回数组num长度并打印
system.out.println(num.size())6、for each遍历数组
i是遍历的数组每一个值,num是数组名。
for(int i:num)
{
System.out.println(i);
}二、输入多个数字
1、正则表达式
不需要import其他的东西。输入一串以空格为间隔的数字,字符串形式,经过正则表达式拆解,存入num动态数组中。
如果数字之间以逗号为间隔,则需要将匹配改为",\\s+"。
import java.util.ArrayList;
ArrayList<Integer> num = new ArrayList<>();
String input= new Scanner(System.in).nextLine();
String[] numbers=input.split("\\s+");
for (String number : numbers)
{
num.add(Integer.parseInt(number));
}2、has.next()方法
该方法存在弊端,不能退出循环。
import java.util.ArrayList;
ArrayList<Integer> num = new ArrayList<>();
Scanner scanner=new Scanner(System.in);
int n;
int[] num;
while(scanner.hasNext()) {
n=scanner.nextInt();
num.add(n);
}三、矩阵连乘
1、什么是矩阵连乘?
不同的结合方式,可以导致不同的数乘次数,因为乘法远大于加法量级,所以加法可以忽视。那什么样的括号选择是可以获得最少的数乘次数呢?

如果一味的进行枚举,寻找最优的数乘次数需要指数级复杂度。显然这种方式,在较大的个数面前利用计算机是不能解决的。

2、动态规划思路
(1)首先定义几个结构,以便后续进行理解。
A[1:n],代表1到n个矩阵的连乘积。
A[i:j]的最少数乘次数记为m[i][j]。
p数组为矩阵链的值。比如30*35和35*15两个矩阵的矩阵链为30,35,15。
s数组记录断开位置。
(2)矩阵连乘遵循最优子结构,也就是说矩阵连乘的各子结构都是最优的。
假设A[1:4]的最优子结构是 ,那么A[1:2]的最优子结构一定是
。
根据上面两条,我们能得出A[i:j]的最少数乘次数记为m[i][j],

3、手推m和s矩阵
m矩阵和s矩阵几乎同步计算,仅保留上三角形,主对角线均为全0,依次按对角线进行计算,每计算完一条对角线向右上平移一条对角线。

下面给出m[1][3]和s[1][3]的计算,可以看到从1断开()小于从2分割(
)的值,所以m[1][3]选择较小者7875,s[1][3]=1。

如果求解A[1:6]的最优解的匹配方式,倒序执行上面s步骤。
4、完整代码
import java.util.Scanner;
import java.util.ArrayList;
public class matrixplusnew {
public static void main(String[] args)
{
ArrayList<Integer> num = new ArrayList<>();
String input= new Scanner(System.in).nextLine();
String[] numbers=input.split("\\s+");
for (String number : numbers)
{
num.add(Integer.parseInt(number));
}
int size=num.size()-1;
//6*6
int [][] m=new int[size+1][size+1];
int [][] s=new int[size+1][size+1];
MatrixChain(num,m,s);
//输出m数组
for(int i=1;i<size+1;i++)
{
for(int j=1;j<size+1;j++)
{
System.out.print(m[i][j]);
System.out.print("\t");
}
System.out.println("");
}
//输出s数组
for(int i=1;i<size+1;i++)
{
for(int j=1;j<size+1;j++)
{
System.out.print(s[i][j]);
System.out.print("\t");
}
System.out.println("");
}
//输出A[1:6]的匹配方式
Traceback(1, 6, s);
}
//m数组和s数组生成
public static void MatrixChain(ArrayList<Integer>p,int [][]m,int [][]s) {
int n = p.size() - 1;
for (int i = 1; i <= n; i++) {
m[i][i] = 0;
}
for (int r = 2; r <= n; r++)
{
for (int i = 1; i <= n - r + 1; i++)
{
int j = i + r - 1; //这个位置非常巧妙,可以确保对角线依次执行
m[i][j] = m[i + 1][j] + p.get(i - 1) * p.get(i) * p.get(j);//由于第二条对角线,依赖于第一条对角线计算m[i][i],m[i][i]值为0,故省略。
s[i][j] = i;
for (int k = i + 1; k < j; k++)
{
int t = m[i][k] + m[k + 1][j] + p.get(i - 1) * p.get(k) * p.get(j);
if (t < m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
//获得括号匹配方式
private static void Traceback(int i,int j,int[][]s)
{
if(i==j)
return;
Traceback(i, s[i][j],s); //单独写每两个子结构的最优解,可以供读者合成匹配方式
Traceback(s[i][j]+1,j,s);
System.out.print("A"+i+", "+s[i][j]);
System.out.println(" and A"+(s[i][j]+1)+", "+j);
}
}
5、备忘录方法
备忘录算法自顶向下计算,但他不够灵活,每次计算完整矩阵链的最优次序。其中p,m数组都为类外数组,所有函数均可使用。通过减少重复计算,减少时间复杂度。

public static int memoizedmatrixChain(int n){
for (int i=0;i<=n;i++){
for(int j=0;j<=n;j++){
m[i][j]=0;
}
}//初始化备忘录数组
return lookupChain(1,n);
}
public static lookupChain(int i,int j){
if(m[i][j]>0)
return m[i][j];//如果该项子问题有记录,返回该记录
if(i==j)
return 0;//如果相乘的两个矩阵相等,则返回0
int u=lookupChain(i+1,j)+p[i-1]*p[i]p[j];//递归调用
s[i][j]=i;//存储最佳断点
for(int k=i+1;k<j;k++){//这里面将断点从i+1开始,可以断链的点直到j-1为止
int t=lookupChain(i,k)+lookupChain(k+1,j)+p[i-1]*p[k]*p[j];
if(t<u){
u=t;
s[i][j]=k;
}
}
m[i][j]=u;
return u;
}
四、凸多边形剖分
凸多边形三角剖分问题类似于矩阵连乘,都是利用动态规划分成子问题,对子问题递归求解。
1、凸多边形形三角剖分原理
通过不同的拆分方法,假设不同边有不同的权值,那么或者不同的组合方式有不同的函数映射,那么不同的三角剖分方式就会存在不同的解,那么最优解怎么求呢?

类比于矩阵连乘的规律,我们也对不同的组合方式加括号表示。最后凸多边形剖分问题也表示为多个子问题叠加的解。

那么根据矩阵连乘,有下面这种最优解的产生形式,可以根据不同的加权的关系写出函数关系,变成矩阵连乘问题。
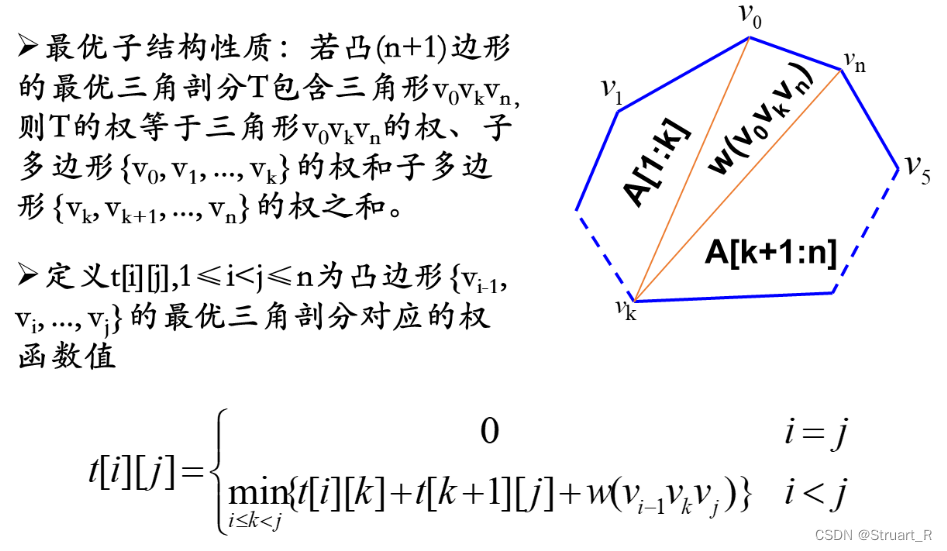
2、完整代码
public class MinWeightTriangulation {
public static void main(String [] args)
{
int size=5;
int m[][]=new int[size+1][size+1];
int s[][]=new int[size+1][size+1];
//定义权值
int num[][]= {{0,2,2,3,1,4},{2,0,1,5,2,3},{2,1,0,2,1,4},{3,5,2,0,6,2},{1,2,1,6,0,1},{4,3,4,2,1,0}};
Triangle(num,m,s);
for(int i=1;i<size+1;i++)
{
for(int j=1;j<size+1;j++)
{
System.out.print(m[i][j]);
System.out.print("\t");
}
System.out.println("");
}
Traceback(1, 5, s);
}
//计算最优值
public static void Triangle(int[][]num,int[][]m,int[][]s)
{
int n=5;
for(int i=1;i<=n;i++)
m[i][i]=0;
for(int r=2;r<=n;r++)
{
for(int i=1;i<=n-r+1;i++)
{
int j=i+r-1;
m[i][j]=m[i+1][j]+Weight(i-1, i, j, num);
s[i][j]=i;
for(int k=i+1;k<j;k++)
{
int t=m[i][k]+m[k+1][j]+Weight(i-1, k, j, num);
if(t<m[i][j])
{
m[i][j]=t;
s[i][j]=k;
}
}
}
}
}
//权重计算
public static int Weight(int i,int j,int k,int[][]num)
{
return num[i][j]+num[j][k]+num[i][k];
}
//返回匹配方式
public static void Traceback(int i,int j,int[][]s)
{
if(i==j)
return;
Traceback(i, s[i][j],s);
Traceback(s[i][j]+1,j,s);
System.out.print("A"+i+", "+s[i][j]);
System.out.println(" and A"+(s[i][j]+1)+", "+j);
}
}




![[管理与领导-108]:IT人看清职场中的隐性规则 - 5 - 你会在不经意间被归属在不同的分类中,一旦分类定型,你就会被打上了某种标签(职场分类方法大全)](https://img-blog.csdnimg.cn/1c3e04878a8e4576a2bb515607f6fdb9.png)


![[Unity][VR]Oculus透视开发图文教程1-Passthrough应用XR项目设置](https://img-blog.csdnimg.cn/9fdc8376906a4b64a472552bcdbc3315.png#pic_center)