贝塞尔曲线
- 1. 本次作业实现的函数及简单描述(详细代码见后)
- 2. 与本次作业有关的基础知识整理
- 3. 代码描述(详细)
- 4. 完整代码
- 5. 参考文献
(本篇为作者学习计算机图形学时根据作业所撰写的笔记, 如有同课程请勿Crtl+c/v )
1. 本次作业实现的函数及简单描述(详细代码见后)
这一块主要介绍本次主要实现的几个函数及其功能
1.bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
可以绘制不止四个点的贝塞尔函曲线,并且处理了反走样问题
升级版: 利用距离比例,进行像素点的判别,解决贝塞尔曲线的反走样问题
2.recursive_bezier(const std::vector<cv::Point2f> &control_points, float t)
根据已有的点vector和给定的t值, 计算出来给定t值对应到贝塞尔曲线上的坐标点
2. 与本次作业有关的基础知识整理
这一部分主要介绍一些跟贝塞尔曲线有关的前置知识,以及贝塞尔曲线的画法
贝塞尔曲线:
Bézier curve(贝塞尔曲线) 是应用于二维图形应用程序的数学曲线。
贝塞尔曲线基础定义:
只要求一定经过起止点,起止点之间的若干控制点用于控制曲线弯曲的方向,最终形成一条经过起止点的光滑曲线被称为贝塞尔曲线。
贝塞尔曲线是线性插值的结果 : “选出两点之间的一个点”
P(t) = P0 + (P1−P0) = (1−t)P0 + t**P1, t∈[0,1] t=P0P1/P0P1
根据控制点的个数,贝塞尔曲线被分为一阶贝塞尔曲线(0个控制点)、二阶贝塞尔曲线(1个控制点)、三阶贝塞尔曲线(2个控制点)等等。(本次实验用到的是三阶贝塞尔曲线(2个控制点))
二阶贝塞尔曲线:
三阶贝塞尔曲线(本次作业需要实现的曲线)
对于贝塞尔曲线,最重要的点是数据点和控制点
数据点: 指一条路径的起始点和终止点。
控制点:控制点决定了一条路径的弯曲轨迹贝塞尔曲线特点:
特点一: 曲线通过始点和终点,并与特征多边形首末两边相切于始点和终点,中间点将曲线拉向自己。
特点二: 平面离散点控制曲线的形状,改变一个离散点的坐标,曲线的形状将随之改变(点对曲线具有整体控制性)。
特点三: 曲线落在特征多边形的凸包之内,它比特征多边形更趋于光滑。特点四: 起始点的方向为响应控制点的切线方向
逐段贝塞尔曲线:
当控制点太多会影响控制点的效果的时候, 我们选择每四个控制点定义一条贝塞尔曲线,然后再将他们连接起来
常见应用场景:
计算机辅助设计和计算机辅助制造应用(CAD/CAM),Adobe Illustrator, Photoshop, Inkscape, Gimp等等。还可以应用在一些图形技术中,像矢量图形(SVG),所以说在可视化学习的重要基础知识。
基本绘制方法: 德卡斯特里奥算法
- 引入参数t (范围为 0~1)
- 取b0到b1, b1到b2上t位置上的点b0’,b1’
- 将b0’,b1’ 连接,取b0’到b1’上t位置上的点b0’’
- 将所有t∈(0,1) 的点都便利一遍相连即可得到贝塞尔曲线
- 若有n个控制点则将上面步骤进行递归操作直到找到最后bn’
解决反走样问题
程序在进行画线时是以点的形式,如果放大有较为明显的不连续,因此可以采用反走样来使其平滑过渡;
对于每一个点,其必然会包含在一个像素之中,可按照比例和着色进行插值,以求得一个较为平滑的过渡;
如下图所示,该点一定会在下图所示的黄色方框内部,而该点离像素点的最远距离为根号2,按照该点到其他四个点的距离进行插值;
3. 代码描述(详细)
这一部分主要介绍实现贝塞尔曲线的各个函数的功能,以及注意要点
de Casteljau的算法来计算贝塞尔曲线的点(步骤如下)
- 计算点的总个数
- 判断点的个数,只有一个点直接返回,多个点的话进行计算
- 递归计算多个点t值对应的贝塞尔曲线上的点,直到计算到最后一个点
cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t)
{
// TODO: Implement de Casteljau's algorithm
int n = control_points.size();
if (n == 1) return control_points[0];
std::vector<cv::Point2f> res_control_points;
for (int i = 0; i < n - 1; i++) {
res_control_points.push_back(cv::Point2f(
(1 - t) * control_points[i].x + t * control_points[i + 1].x,
(1 - t) * control_points[i].y + t * control_points[i + 1].y));
}
return recursive_bezier(res_control_points, t);
}
基础版贝塞尔: (简单的将所给点画出)
- 对每个t值循环计算出来对应的点然后进行绘制
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
for (double t = 0.0; t <= 1.0; t += 0.001) // 循环得到点,并记录输出
{
cv::Point2f point = recursive_bezier(control_points, t);
window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
}
}
升级版贝塞尔(可以解决曲线的反走样问题)
- 先找到根据t值计算出来的贝塞尔曲线上的点,其周围四个坐标
- 计算该点到周围四个像素点的距离,距离越大,颜色应该越浅 {max-distance}
- 按照distance/sum(distance)重新给四个点的像素赋值,并与原始色素的值进行比较,不能超过255.
- 根据计算出来的点和对应的像素值进行重新绘制
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
for (float t = 0.0; t <= 1.0; t = t + 0.001)
{
cv::Point2f point = recursive_bezier(control_points, t); //接收每一个t所求得的点
//找到该点周围的四个点坐标,先找到一个右上的顶点,然后其他的通过这个点求出
cv::Point2f point_1 = cv::Point2f(point.x - std::floor(point.x) < 0.5 ? std::floor(point.x) : std::ceil(point.x), //右上的点
point.y - std::floor(point.y) < 0.5 ? std::floor(point.y) : std::ceil(point.y));
cv::Point2f point_2 = cv::Point2f(point_1.x - 1.0, point_1.y);
cv::Point2f point_3 = cv::Point2f(point_1.x - 1.0, point_1.y - 1.0);
cv::Point2f point_4 = cv::Point2f(point_1.x, point_1.y - 1.0);
//用vector容器存储刚刚求得的四个像素点坐标;
std::vector<cv::Point2f> distance_dot{ point_1,point_2,point_3,point_4 };
float MaxDistance = sqrt(2.0);
float SumDistance = 0.0f;
float pi_distance = 0.0f;
std::vector<float> distance_List = {};
window.at<cv::Vec3b>(point.y, point.x)[1] = 255;//Mat.at<存储类型名称>(行,列)[通道]
for (int i = 0; i < 4; i++)
{
cv::Point2f point_coordinate(distance_dot[i].x + 0.5, distance_dot[i].y + 0.5);//记录像素中心点;
// 距离像素点越近的点 实际上和颜色占比应该越小 因此采用 max-实际距离 的方法进行数据预处理
pi_distance = MaxDistance - sqrt(std::pow(point.x - point_coordinate.x, 2) + std::pow(point.y - (point_coordinate.y), 2));
distance_List.push_back(pi_distance);
SumDistance += pi_distance; // 计算一个总的距离值
}
for (int i = 0; i < 4; i++)
{
float d = distance_List[i] / SumDistance; // d是距离比例系数
window.at<cv::Vec3b>(distance_dot[i].y, distance_dot[i].x)[1] = std::min(255.f, window.at<cv::Vec3b>(distance_dot[i].y, distance_dot[i].x)[1] + 255.f * d);
//不超过255.f,要进行最小值比较
}
}
}
4. 完整代码
#include <chrono>
#include <iostream>
#include <opencv2/opencv.hpp>
std::vector<cv::Point2f> control_points;
void mouse_handler(int event, int x, int y, int flags, void *userdata)
{
if (event == cv::EVENT_LBUTTONDOWN)
{
std::cout << "Left button of the mouse is clicked - position (" << x << ", "
<< y << ")" << '\n';
control_points.emplace_back(x, y);
}
}
void naive_bezier(const std::vector<cv::Point2f> &points, cv::Mat &window)
{
auto &p_0 = points[0];
auto &p_1 = points[1];
auto &p_2 = points[2];
auto &p_3 = points[3];
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = std::pow(1 - t, 3) * p_0 + 3 * t * std::pow(1 - t, 2) * p_1 +
3 * std::pow(t, 2) * (1 - t) * p_2 + std::pow(t, 3) * p_3;
window.at<cv::Vec3b>(point.y, point.x)[2] = 255;
}
}
cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t)
{
// TODO: Implement de Casteljau's algorithm
int n = control_points.size();
if (n == 1) return control_points[0];
std::vector<cv::Point2f> res_control_points;
for (int i = 0; i < n - 1; i++) {
res_control_points.push_back(cv::Point2f(
(1 - t) * control_points[i].x + t * control_points[i + 1].x,
(1 - t) * control_points[i].y + t * control_points[i + 1].y));
}
return recursive_bezier(res_control_points, t);
}
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
for (float t = 0.0; t <= 1.0; t = t + 0.001)
{
cv::Point2f point = recursive_bezier(control_points, t); //接收每一个t所求得的点
//找到该点周围的四个点坐标,先找到一个右上的顶点,然后其他的通过这个点求出
cv::Point2f point_1 = cv::Point2f(point.x - std::floor(point.x) < 0.5 ? std::floor(point.x) : std::ceil(point.x), //右上的点
point.y - std::floor(point.y) < 0.5 ? std::floor(point.y) : std::ceil(point.y));
cv::Point2f point_2 = cv::Point2f(point_1.x - 1.0, point_1.y);
cv::Point2f point_3 = cv::Point2f(point_1.x - 1.0, point_1.y - 1.0);
cv::Point2f point_4 = cv::Point2f(point_1.x, point_1.y - 1.0);
//用vector容器存储刚刚求得的四个像素点坐标;
std::vector<cv::Point2f> distance_dot{ point_1,point_2,point_3,point_4 };
float MaxDistance = sqrt(2.0);
float SumDistance = 0.0f;
float pi_distance = 0.0f;
std::vector<float> distance_List = {};
window.at<cv::Vec3b>(point.y, point.x)[1] = 255;//Mat.at<存储类型名称>(行,列)[通道]
for (int i = 0; i < 4; i++)
{
cv::Point2f point_coordinate(distance_dot[i].x + 0.5, distance_dot[i].y + 0.5);//记录像素中心点;
// 距离像素点越近的点 实际上和颜色占比应该越小 因此采用 max-实际距离 的方法进行数据预处理
pi_distance = MaxDistance - sqrt(std::pow(point.x - point_coordinate.x, 2) + std::pow(point.y - (point_coordinate.y), 2));
distance_List.push_back(pi_distance);
SumDistance += pi_distance; // 计算一个总的距离值
}
for (int i = 0; i < 4; i++)
{
float d = distance_List[i] / SumDistance; // d是距离比例系数
window.at<cv::Vec3b>(distance_dot[i].y, distance_dot[i].x)[1] = std::min(255.f, window.at<cv::Vec3b>(distance_dot[i].y, distance_dot[i].x)[1] + 255.f * d);
//不超过255.f,要进行最小值比较
}
}
}
int main()
{
cv::Mat window = cv::Mat(700, 700, CV_8UC3, cv::Scalar(0));
cv::cvtColor(window, window, cv::COLOR_BGR2RGB);
cv::namedWindow("Bezier Curve", cv::WINDOW_AUTOSIZE);
cv::setMouseCallback("Bezier Curve", mouse_handler, nullptr);
int key = -1;
while (key != 27)
{
window.setTo(0);
for (auto &point : control_points)
{
cv::circle(window, point, 3, {255, 255, 255}, 3);
}
if (control_points.size() >= 4)
{
naive_bezier(control_points, window); // 所有点的绘制的贝塞尔曲线用绿色表示
bezier(control_points, window); // 前四个点绘制的贝塞尔曲线用红色显示
cv::imshow("Bezier Curve", window);
cv::imwrite("my_bezier_curve.png", window);
key = cv::waitKey(1);
}
cv::imshow("Bezier Curve", window);
key = cv::waitKey(20);
}
return 0;
}
5. 参考文献
1. 贝塞尔曲线
2. opencv 处理鼠标事件的方法
3. 贝塞尔曲线简单介绍
4. 解决反走样问题


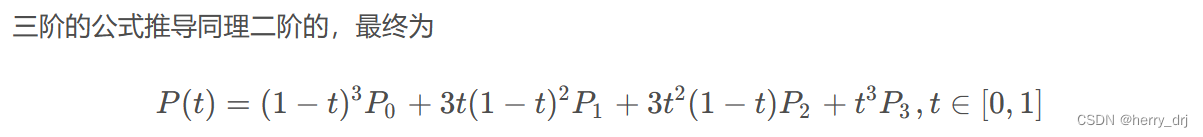





![P1541 [NOIP2010 提高组] 乌龟棋(4维背包问题)](https://img-blog.csdnimg.cn/d9a4e663e5c4435c9aa9d606503f814c.png)







![[Linux] 4.常用初级指令](https://img-blog.csdnimg.cn/11dc8a0f42b04eb5ac3aae7ee1b0c4e8.png)