[NOIP2012 提高组] 开车旅行

题目描述

小 $\text{A}$ 和小 $\text{B}$ 决定利用假期外出旅行，他们将想去的城市从 $1 $ 到 $n$ 编号，且编号较小的城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 $i$ 的海拔高度为$h_i$，城市 $i$ 和城市 $j$ 之间的距离 $d_{i,j}$ 恰好是这两个城市海拔高度之差的绝对值，即 $d_{i,j}=|h_i-h_j|$。

旅行过程中，小 $\text{A}$ 和小 $\text{B}$ 轮流开车，第一天小 $\text{A}$ 开车，之后每天轮换一次。他们计划选择一个城市 $s$ 作为起点，一直向东行驶，并且最多行驶 $x$ 公里就结束旅行。

小 $\text{A}$ 和小 $\text{B}$ 的驾驶风格不同，小 $\text{B}$ 总是沿着前进方向选择一个最近的城市作为目的地，而小 $\text{A}$ 总是沿着前进方向选择第二近的城市作为目的地（注意：本题中如果当前城市到两个城市的距离相同，则认为离海拔低的那个城市更近）。如果其中任何一人无法按照自己的原则选择目的城市，或者到达目的地会使行驶的总距离超出 $x$ 公里，他们就会结束旅行。

在启程之前，小 $\text{A}$ 想知道两个问题：

1、 对于一个给定的 $x=x_0$，从哪一个城市出发，小 $\text{A}$ 开车行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值最小（如果小 $\text{B}$ 的行驶路程为 $0$，此时的比值可视为无穷大，且两个无穷大视为相等）。如果从多个城市出发，小 $\text{A}$ 开车行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值都最小，则输出海拔最高的那个城市。

2、对任意给定的 $x=x_i$ 和出发城市 $s_i$，小 $\text{A}$ 开车行驶的路程总数以及小 $\text{B}$ 行驶的路程总数。

输入格式

第一行包含一个整数 $n$，表示城市的数目。

第二行有 $n$ 个整数，每两个整数之间用一个空格隔开，依次表示城市 $1$ 到城市 $n$ 的海拔高度，即 $h_1,h_2...h_n$，且每个 $h_i$ 都是互不相同的。

第三行包含一个整数 $x_0$。

第四行为一个整数 $m$，表示给定 $m$ 组 $s_i$ 和 $x_i$。

接下来的 $m$ 行，每行包含 $2$ 个整数 $s_i$ 和 $x_i$，表示从城市$s_i$ 出发，最多行驶 $x_i$ 公里。

输出格式

输出共 $m+1$ 行。

第一行包含一个整数 $s_0$，表示对于给定的 $x_0$，从编号为 $s_0$ 的城市出发，小 $\text{A}$ 开车行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值最小。

接下来的 $m$ 行，每行包含 $2$ 个整数，之间用一个空格隔开，依次表示在给定的 $s_i$ 和 $x_i$ 下小 $\text{A}$ 行驶的里程总数和小 $\text{B}$ 行驶的里程总数。

样例 #1

样例输入 #1

4 
2 3 1 4 
3 
4 
1 3 
2 3 
3 3 
4 3

样例输出 #1

1 
1 1 
2 0 
0 0 
0 0

样例 #2

样例输入 #2

10 
4 5 6 1 2 3 7 8 9 10 
7 
10 
1 7 
2 7 
3 7 
4 7 
5 7 
6 7 
7 7 
8 7 
9 7 
10 7

样例输出 #2

2 
3 2 
2 4 
2 1 
2 4 
5 1 
5 1 
2 1 
2 0 
0 0 
0 0

提示

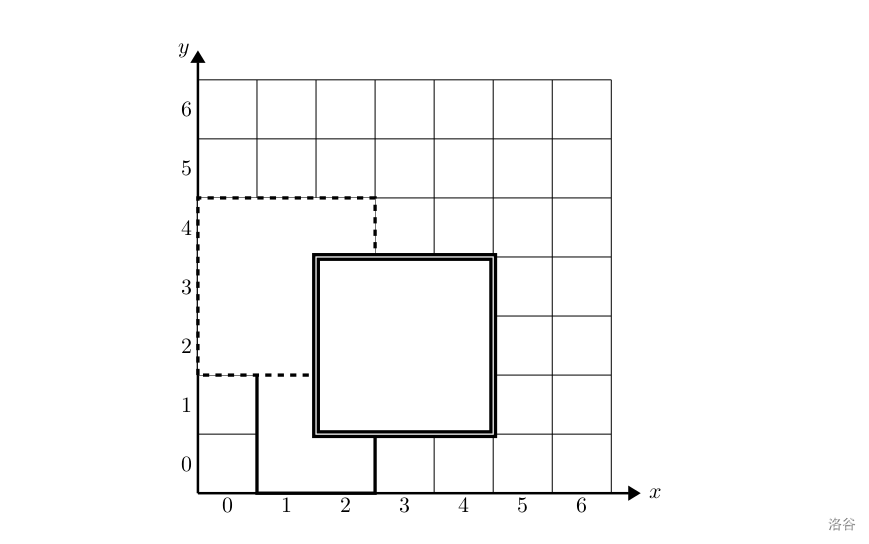
【样例1说明】

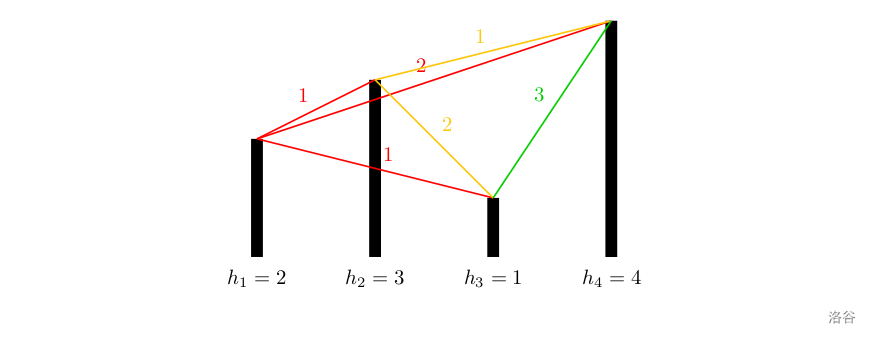
各个城市的海拔高度以及两个城市间的距离如上图所示。

如果从城市 $1$ 出发，可以到达的城市为 $2,3,4$，这几个城市与城市 $1$ 的距离分别为 $1,1,2$，但是由于城市 $3$ 的海拔高度低于城市 $2$，所以我们认为城市 $3$ 离城市 $1$ 最近，城市 $2$ 离城市 $1$ 第二近，所以小A会走到城市 $2$。到达城市 $2$ 后，前面可以到达的城市为 $3,4$，这两个城市与城市 $2$ 的距离分别为 $2,1$，所以城市 $4$ 离城市 $2$ 最近，因此小B会走到城市$4$。到达城市 $4$ 后，前面已没有可到达的城市，所以旅行结束。

如果从城市 $2$ 出发，可以到达的城市为 $3,4$，这两个城市与城市 $2$ 的距离分别为 $2,1$，由于城市 $3$ 离城市 $2$ 第二近，所以小 $\text{A}$ 会走到城市 $3$。到达城市 $3$ 后，前面尚未旅行的城市为 $4$，所以城市 $4$ 离城市 $3$ 最近，但是如果要到达城市 $4$，则总路程为 $2+3=5>3$，所以小 $\text{B}$ 会直接在城市 $3$ 结束旅行。

如果从城市 $3$ 出发，可以到达的城市为 $4$，由于没有离城市 $3$ 第二近的城市，因此旅行还未开始就结束了。

如果从城市 $4$ 出发，没有可以到达的城市，因此旅行还未开始就结束了。

【样例2说明】

当 $x=7$ 时，如果从城市 $1$ 出发，则路线为 $1\to 2\to 3\to 8\to 9$，小 $\text{A}$ 走的距离为 $1+2=3$，小 $\text{B}$ 走的距离为 $1+1=2$。（在城市 $1$ 时，距离小 $\text{A}$ 最近的城市是 $2$ 和 $6$，但是城市 $2$ 的海拔更高，视为与城市 $1$ 第二近的城市，所以小 $\text{A}$ 最终选择城市 $2$；走到$9$ 后，小 $\text{A}$ 只有城市 $10$ 可以走，没有第二选择可以选，所以没法做出选择，结束旅行）

如果从城市 $2$ 出发，则路线为 $2\to 6\to 7$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为 $2,4$。

如果从城市 $3$ 出发，则路线为 $3\to 8\to 9$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$2,1$。

如果从城市 $4$ 出发，则路线为 $4\to 6\to 7$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为 $2,4$。

如果从城市 $5$ 出发，则路线为 $5\to 7\to 8$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为 $5,1$。

如果从城市 $6$ 出发，则路线为 $6\to 8\to 9$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$5,1$。

如果从城市 $7$ 出发，则路线为 $7\to 9\to 10$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$2,1$。

如果从城市 $8$ 出发，则路线为 $8\to 10$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$2,0$。

如果从城市 $9$ 出发，则路线为 $9$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为 $0,0$（旅行一开始就结束了）。

如果从城市 $10$ 出发，则路线为 $10$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$0,0$。

从城市 $2$ 或者城市 $4$ 出发小 $\text{A}$ 行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值都最小，但是城市 $2$ 的海拔更高，所以输出第一行为 $2$。

【数据范围与约定】

对于 $30\%$ 的数据，有$1\le n\le 20,1\le m\le 20$；
对于$40\%$ 的数据，有$1\le n\le 100,1\le m\le 100$；
对于 $50\%$ 的数据，有$1\le n\le 100,1\le m\le 1000$；
对于 $70\%$ 的数据，有$1\le n\le 1000,1\le m\le 10^4$；
对于 $100\%$ 的数据：$1\le n,m\le 10^5$，$-10^9\le h_i\le 10^9$，$1\le s_i\le n$，$0\le x_i\le 10^9$
数据保证 $h_i$ 互不相同。

完整代码

#include<iostream>
#include<cstdio>
#include<cmath>
#include<set>
using namespace std;
const int N=1e5+200,INF=2e9;
struct City
{
	int id,al;//identifier,altitude
	friend bool operator < (City a,City b)
    {
        return a.al<b.al; 
    }
};
int n,m,x0,la,lb,ansid;
int h[N],s[N],x[N];
int f[20][N][5],da[20][N][5],db[20][N][5];
double ans=INF*1.0;
multiset<City> q;
void calc(int S,int X)
{
	int p=S;
	la=0,lb=0;
	for(int i=18;i>=0;i--)
		if(f[i][p][0] && la+lb+da[i][p][0]+db[i][p][0]<=X)
		{
			la+=da[i][p][0];
			lb+=db[i][p][0];
			p=f[i][p][0];
		}
}
void pre()
{
	h[0]=INF,h[n+1]=-INF;
	City st;//start
	st.id=0,st.al=INF;
	q.insert(st),q.insert(st);
	st.id=n+1,st.al=-INF;
	q.insert(st),q.insert(st);
	for(int i=n;i;i--)
	{
		int ga,gb;
		City now;
		now.id=i,now.al=h[i];
		q.insert(now);
		set<City>::iterator p=q.lower_bound(now);
		p--;
		int lt=(*p).id,lh=(*p).al;//last
		p++,p++;
		int ne=(*p).id,nh=(*p).al;//next
		p--;
		if(abs(nh-h[i])>=abs(h[i]-lh))
		{
			gb=lt;
			p--,p--;
			if(abs(nh-h[i])>=abs(h[i]-(*p).al))
				ga=(*p).id;
			else
				ga=ne;
		}
		else
		{
			gb=ne;
			p++,p++;
			if(abs((*p).al-h[i])>=abs(h[i]-lh))
				ga=lt;
			else
				ga=(*p).id;
		}//2、预处理
		f[0][i][0]=ga,f[0][i][1]=gb;
		da[0][i][0]=abs(h[i]-h[ga]);
		db[0][i][1]=abs(h[i]-h[gb]);//3、DP初值
	}
	for(int i=1;i<=18;i++)
		for(int j=1;j<=n;j++)
			for(int k=0;k<2;k++)
				if(i==1)
				{
					f[1][j][k]=f[0][f[0][j][k]][1-k];
					da[1][j][k]=da[0][j][k]+da[0][f[0][j][k]][1-k];
					db[1][j][k]=db[0][j][k]+db[0][f[0][j][k]][1-k];	
				}
				else
				{
					f[i][j][k]=f[i-1][f[i-1][j][k]][k];
					da[i][j][k]=da[i-1][j][k]+da[i-1][f[i-1][j][k]][k];
					db[i][j][k]=db[i-1][j][k]+db[i-1][f[i-1][j][k]][k];
				}//3、倍增优化DP
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		scanf("%d",&h[i]);
	cin>>x0>>m;
	for(int i=1;i<=m;i++)
		scanf("%d%d",&s[i],&x[i]);//1、输入
	pre();
	for(int i=1;i<=n;i++)
	{
		calc(i,x0);
		double nowans=(double)la/(double)lb;
		if(nowans<ans)
		{
			ans=nowans;
			ansid=i;
		}
		else
			if(nowans==ans && h[ansid]<h[i])
				ansid=i;
	}
	cout<<ansid<<endl;//4、求解问题1
	for(int i=1;i<=m;i++)
	{
		calc(s[i],x[i]);
		printf("%d %d\n",la,lb);
	}//5、求解问题2
	return 0;
}