引言

• 向量在计算机图形学、碰撞检测和物理模拟中扮演者关键的角色。因此在游戏开发之前我们必须先了解向量。
• 本章研究向量的使用。

一、向量

• 如果你对数学中的向量不太熟悉，建议阅读《3D数学基础：图形和游戏开发 第2版》，如果你需要某些PDF资源，可以找我😊

（1）向量的简介

• 向量是一种具备大小和方向的量。普通的浮点数如 (3.0) 可以看作是一维向量，屏幕上的坐标如 (200，400) 可以看作是二维向量，三维空间中的点如 (100，200，500) 可以看作是三维向量。
• 向量表示一种方向性，它也有自身的大小，向量还具有平移性。
• 向量具有起点和终点，当然这都是可以平移的。如果一个向量的起点位于坐标系的原点，那么我们就说这个向量位于标准位置。

（2）向量的使用

• 空间具有相对性，因此在度量一切事物之前我们都要建立坐标系，在特点的坐标系下的向量才是有意义的，不同坐标系中同一个向量的代数值不同。
• 要记住在三维空间中讨论任何事情，都要先确定是处于什么坐标系下。当然不同坐标系之间可以进行转换。
• 一个三维向量 (x,y,z) 可以表示点，也可以表示向量，这完全取决于你在编程中怎样认为它。所以在编程中如果我们编写了一个类Vector3，即一个三维向量，那么你可以这样做：

typedef Vector3 Point;

• 很直观对吧，这样在你要使用向量时就用Vector3，在你要使用点时就使用Point。当然在游戏编程中我们通常不这样做，因为我们是可以区分一个变量是点还是向量，这一般取决于这个变量的名字，如果它带有position，则很明显表示位置，否则表示向量。因此在往后对变量的命名时，名称必须能清晰表达其内容。

（3）左手坐标系和右手坐标系

• 向量A叉乘向量B会得到向量C，向量C同时垂直于A和B。我们一般通过左手或右手定则来判断叉乘结果即C的方向。
• Direct3D采用左手坐标系，在左手坐标系中，有A叉乘B等于C。那么现在请你伸出左手，四指指向A的方向（比如你的正前方），然后将四指朝掌心弯曲直到指向B的方向（比如你的正右方），最终你大拇指所指的方向就是C的方向（即你的正上方）。
• 如果你换一只手，你会发现你无法将四指旋转到你的正右方，如果你将右手大拇指朝下，再旋转四指就可以旋转到正右方，此时你的大拇指向下，即C的方向向下。
• 由上可知左右手坐标系叉乘的结果是相反的，即C的方向是不同的。
• 在三维空间中，x轴、y轴、z轴两两相互垂直，许多时候我们会通过叉乘其中两者求得另一者。有时x=y叉乘z，而有时x=z叉乘y。这完全取决于指定的坐标系是左手还是右手。当然没有必要计较那么多，左右只是规定没有好坏之分，我们学习的Direct3D采用左手坐标系，记住这一点就好了。

（4）向量运算理论

• 向量可以进行许多运算，包括：向量与常数的乘除法，向量与向量的加减法，向量与向量的点乘和叉乘。
• 向量和常数的乘除法：向量的每个分量和常数相乘除。
• 向量间加减法：向量的每个分量彼此相加减。
• 向量间点乘：向量的每个分量相乘再相加。
• 向量间叉乘：根据叉乘公式。
• 向量的正交化：向量自身减去在对方上的投影。
• 向量的长度：向量各分量平方再开根。
• 向量的单位向量：向量各分量除以向量的长度。

（5）向量运算实践

• 不妨写一个向量类看看？我很喜欢写基础性代码，下面是我写的向量类代码，请你看看有没有什么问题，如果有欢迎在评论区留言😊

// 向量类的实现
template<typename T>
struct Vector3
{
	// 向量类的构造函数
	Vector3<T>() :x(0), y(0), z(0) {}
	Vector3<T>(T _x, T _y, T _z) : x(_x), y(_y), z(_z) {}

	// 向量和常数的乘除法：向量的每个分量和常数相乘除。
	Vector3<T> operator*(const T value)const
	{
		return Vector3<T>(this->x * value, this->y * value, this->z * value);
	}
	Vector3<T> operator/(const T value)const
	{
		return Vector3<T>(this->x / value, this->y / value, this->z / value);
	}


	// 向量间加减法：向量的每个分量彼此相加减。
	Vector3<T> operator+(const Vector3<T>& vect)const
	{
		return Vector3<T>(this->x + vect.x, this->y + vect.y, this->z + vect.z);
	}
	Vector3<T> operator-(const Vector3<T>& vect)const
	{
		return Vector3<T>(this->x - vect.x, this->y - vect.y, this->z - vect.z);
	}

	// 向量间点乘：向量的每个分量相乘再相加。
	T Dot(const Vector3<T>& vect)const
	{
		return (this->x * vect.x + this->y * vect.y + this->z * vect.z);
	}

	// 向量间叉乘：根据叉乘公式。
	T Cross(const Vector3<T>& vect)const
	{
		return (
			this->y * vect.z - this->z * vect.y,
			this->z * vect.x - this->x * vect.z,
			this->x * vect.y - this->y * vect.x);
	}

	// 向量的长度：向量各分量平方再开根。
	T getLength()const
	{
		return sqrt(this->x * this->x + this->y * this->y + this->z * this.z);
	}

	// 向量的单位向量：向量各分量除以向量的长度。
	Vector3<T> getNormalizeVect()const
	{
		T length = getLength();
		return (*this) / T;
	}

	// 向量的正交化：向量自身减去在对方上的投影。
	void orthogonal(Vector3<T> vect)const
	{
		*this =  (*this) - (*this).Cross(vect) * vect / vect.getLength() / vect.getLength();
		// 设有向量A和B，其长度分别为||A||和||B||，其对应单位向量为nA和nB，它们间夹角为ct
		// A点乘B = ||A|| * ||B|| * cos(ct)
		// A在B上的投影 = ||A|| * nB * cos(ct)
		//              = ||A|| * B / ||B|| * cos(ct)
		//              = A点乘B * B / ||B|| / ||B||
	}

	union 
	{
		T data[3];
		T x, y, z;
	};
};

（6）SIMD指令与union

• 你可能主要到对于向量类数据的定义我使用了union，为什么要这样呢？
• 因为对于使用向量类的用户即程序员来说，你在写代码时有时希望向量的各个分量是独立的，这样你可以获取vect.x和vect.y，很自由吧。但是有时你又希望向量的数据是个整体数组，这样你就可像使用指针一样自由的使用data传递参数，使用函数等。因此使用共用体是非常方便的，相当于我们类的数据结构有多种不同的解读方式。
• 通常CPU一次运算只能算个：(a+b) 或者 (a-b)，这样我们的两个向量加或减一次，CPU都要计算多次，这很耗费性能。于是构建CPU的人发明出了一些指令，使得CPU一次可以计算：(a1+b1, a2+b2, a3+b3)，这样我们的向量运算速度就会成倍提示。这些指令就叫做SIMD。
• SIMD需要参数的一种类型是 __m128，这种变量有128个字节，你可以存储任意数据只要不超过128字节就行，比如我们将上文中(a1,a2,a3)存储到一个 __m128中，就可以与另一个 __m128变量运算。但是出现了一个问题，我们如何将我们的Vector3转换为 __m128呢？这个转换的时间是不可避免的代价，如果处理不好，将导致使用SIMD还不如不使用，因为代价的时间超过了补偿提升性能的时间，导致得不偿失。

（7）DirectXMath中的SIMD

• DirectXMath是一款为Direct3D应用程序专门打造的3D数学库，Windows8及其以上版本都会在自身的Windows SDK中包含DirectXMath。
• DirectXMath采用了 SIMD流指令扩展2 (Streaming SIMD Extensions2 ,简写为SSE2) 指令集。借助128位宽的单指令多数据 (SIMD) 寄存器，利用一条SIMD指令即可同时对4个32位浮点数或整数进行运算，这将极大的提高运算性能。
• 如果你想查找有关DirectXMath的信息，可以在MSDN上查找其在线文档。如果你想提高SIMD设计一个向量库，可以参考Designing Fast Cross-Platform SIMD Vector Libraries。如果你想了解SIMD，我更推荐你先看一下SIMD简介。
• SIMD如今的发展已经很快了，不仅仅具有128位寄存器，正如下图所示还发展出了256和512位寄存器，这代表一次最多可以计算16个32位浮点数。这个数字对于向量来说可能太多了，但是对于矩阵来说就刚好可以利用。
  
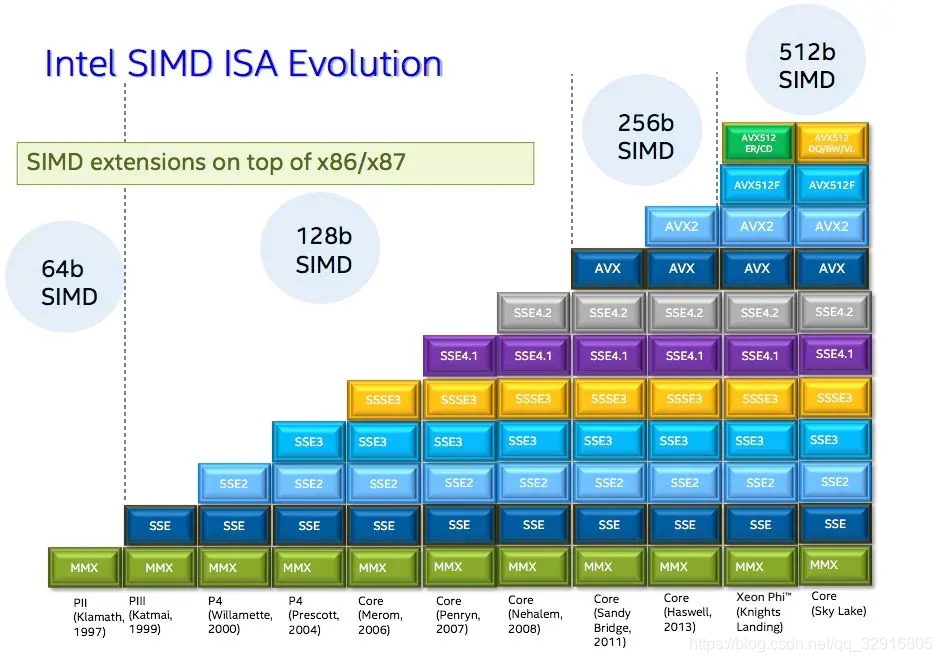
• 极致的性能是每一个男人的追求，理论上最高的512位浮点数可以提高16倍CPU的运算速度，是不是非常诱人？当然我的CPU最高仅支持AVX2，即我最高只能使用256位寄存器，如果你想查看你的CPU支持哪些SIMD指令集，只需要下载软件CPU-Z即可查看。
• 理论上SIMD可以提高数倍CPU的性能。但实际中并非如此，SIMD寄存器位数和对应变量的类型如下图所示：

SIMD寄存器位数	对应变量类型
128	__m128
256	__m256
512	__m512

• 64位太low了我就不写了哈。我们使用SIMD提升性能最需要注意的就是类型转换的代价，例如我们使用__m128类型计算向量运算，我们需要先将向量转换为__m128，使用__m128运算后，我们还要将结果类型__m128转换为向量，因此这两次转换就是我们最需要注意的地方。如果转换不好，则性能提升倍数会下降，甚至性能不如不使用SIMD。
• 向量类和SIMD寄存器对应类型之间的转换都要依靠SIMD中的函数实现，有些函数对应一条汇编语言，而有些函数对应多条汇编语言，这会导致性能的差距，因此在选用函数时一定要注意。SIMD小试牛刀的代码可以查看我的这篇文章SIMD初试。
• 对于x86平台需要在项目属性中手动启用SSE2指令集，对于x64位系统则不必开启SSE2指令集，因为所有的x64CPU对此均有支持。

二、 DirectXMath中的向量

（1）XMVECTOR和XMFLOATn

• 在DirectXMath中，核心的向量类型是XMVECTOR，它将被映射到SIMD硬件寄存器。在开启SSE2后，XMVECTOR类型的定义如下所示：

using XMVECTOR = __m128;

• 可见在DirectXMath中核心的向量类其实就是SIMD中的寄存器类型。
• XMVECTOR类型的数据需要按照16字节对齐，这对于局部变量和全局变量都是自动实现的，而对于在类中定义的XMVECTOR类型数据却不会。
• 对于在类中需要定义向量成员属性的情况，应该使用XMFLOATn类进行定义。XMFLAOT3类型的定义如下：

    struct XMFLOAT3
    {
        float x;
        float y;
        float z;

        XMFLOAT3() = default;

        XMFLOAT3(const XMFLOAT3&) = default;
        XMFLOAT3& operator=(const XMFLOAT3&) = default;

        XMFLOAT3(XMFLOAT3&&) = default;
        XMFLOAT3& operator=(XMFLOAT3&&) = default;

        constexpr XMFLOAT3(float _x, float _y, float _z) noexcept : x(_x), y(_y), z(_z) {}
        explicit XMFLOAT3(_In_reads_(3) const float* pArray) noexcept : x(pArray[0]), y(pArray[1]), z(pArray[2]) {}
    };

• 可以看到DirectXMath库中定义的XMFLOATn就是一副“空壳”，因为它仅定义了三维向量所具有的数据xyz、构造函数和赋值函数，而没有定义向量的任何一种运算，没有实现向量的加减乘除等任意一种功能。
• 上述的解释是DirectXMath是使用XMVECTOR类型进行向量运算的，也就是说其他XMFLOATn类型要进行向量运算，就必须先转换为XMVECTOR，运算完之后可能还需要将结果转换回XMFLOATn。
• 既然本质都是使用XMVECTOR进行运算，为什么不将XMFLOATn类型直接定义为XMVECTOR类型呢？原因在上文我们已经讲过了，因为XMVECTOR即__m128这种SIMD寄存器类型变量必须要按照16字节对齐，否则就无法达到使用SIMD的条件。当要使用的向量为全局变量或者局部变量时，XMVECTOR变量会自动对齐，因此可以直接使用。而当使用的向量为类中的成员属性时，XMVECTOR变量不会自动对齐，定义了也没有用，因此使用另一种类XMFLOATn作代替。
• 直接使用XMFLOAT128代替XMVECTOR不是即可，为什么要定义多种类型XMFLOATn呢？因为在实际的游戏中，比如你看到满屏幕的弹性球那种画面，每个游戏对象都包含了多个向量属性，在成千上万个游戏对象的情况下，这些对象占用的内存空间是很大的，因此我们要尽量节省每个对象的空间，而节省每个对象的空间就是节省每个对象向量所包含的字节数。XMFLOAT类型占用128个字节，这是CPU开发者规定的，当我们要使用时就必须分配128个字节进行运算。但是在类中记录向量时通常需要很少的字节，比如位置向量就只需要32*3=96个字节，而屏幕坐标等向量只需要64个字节，当然是能省则省，因此将XMFLOAT分化为XMFLOATn。
• 所以总结一下：
   1. 局部变量和全局变量使用XMVECTOR类型。
   2. 类中的数据成员使用XMFLOATn类型。
   3. 运算XMFLOATn类型分为三步：
    （1） 将XMFLOATn转换为XMVECTOR。
    （2）使用XMVECTOR进行运算。
    （3）将XMVECTOR转换回XMFLAOTn。

（2）初试XMVECTOR和XMFLOATn

• 学习编程要写代码，不妨在你的项目源文件中新建一个Test.cpp，并在其中编写main函数来编写代码。当然一山不容二虎，如果你现在启动，只能启动到BoxApp.cpp里面的main函数。那么怎么办呢？右键BoxApp.cpp，点击最下面的选项【属性】，再将【从生成中排除】选择为【是】，如下图所示：
  
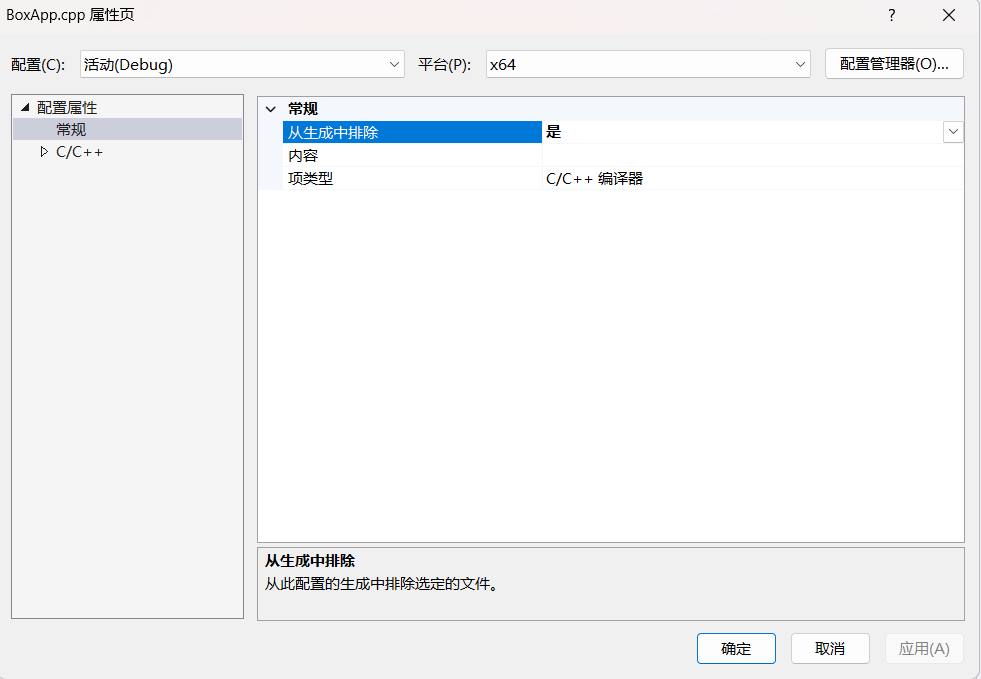
• 好了你现在再运行项目就会启动你Test.cpp里面的main函数了，让我们来编写测试代码吧，如下：

#define _CRT_SECURE_NO_WARNINGS  // 重定向输入输出(否则默认是没有控制台窗口，你也就看不到输出了，此宏必须写在头文件引用之前！)

#include<windows.h>				 // Windows API编程所需头文件
#include<DirectXMath.h>			 // DirectXMath库
#include<iostream>

// Windows API编程的main函数为WinMain，照着写就是了
int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE prevInstance,
	PSTR cmdLine, int showCmd)
{
	// 这三行代码启动一个控制台，让你的cou和cin绑定控制台
	AllocConsole();
	freopen("CONOUT$", "w", stdout);
	freopen("CONIN$", "r", stdin);

	// 定义一个XMVECTOR实例试试
	DirectX::XMVECTOR xmvector;
	
	// 由于XMVECTOR即__m128为128位寄存器，所以可以按照不同方式解析数据
	// .m128_f32表示将其解析为：存储32位浮点数的数组，然后按照[index]的形式索引即可得到分量xyzw
	for (int i = 0; i < 4; i++)
		std::cout << xmvector.m128_f32[i] << std::endl;
	
	// 分别定义XMFLAOTn类型
	DirectX::XMFLOAT2 xmfloat2;
	DirectX::XMFLOAT4 xmflaot4 = DirectX::XMFLOAT4();

	xmfloat2.x = 1;
	std::cout << xmfloat2.x << std::endl;
	std::cout << xmflaot4.x << " " << xmflaot4.y << " " << xmflaot4.z << " " << xmflaot4.w;

	while (1); // 阻止程序终止导致控制台关闭无法看到输出信息
	return 0;
}

• 运行结果如下：
  
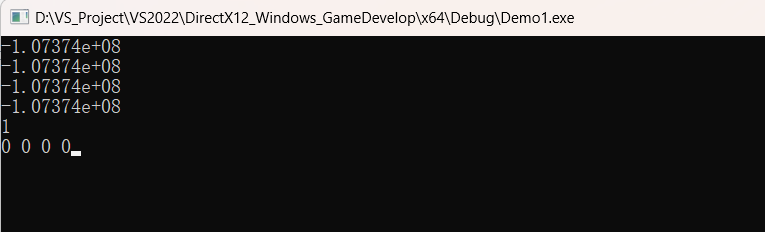
• 需要注意的是，由输出可知：
   1. 直接定义的XMVECTOR即__m128，其数据是未初始化即不为零的。
   2. 未显示初始化的XMFLOATn变量是无法使用的。上文中我将xmfloat2.x赋值为1，你可以尝试删掉这条语句，程序会报错。即XMVECTOR未显示初始化可使用但值未知，XMFLOATn未显示初始化不可使用否则程序报错。

（3）XMVECTOR和XMFLOATn的互相转换

【1】XMVECTOR和XMFLAOTn之间的直接转换

• 在学习向量运算之前，我们还是先学习一下两种类型之间的转换，即上文运算XMFLOATn步骤中的第一步和第三步。
• 先学习将XMFLOATn类型转换为XMVECTOR类型：

inline XMVECTOR XM_CALLCONV XMLoadFloat2(const XMFLOAT2* pSource) noexcept
{
    assert(pSource);
#if defined(_XM_NO_INTRINSICS_)
    XMVECTOR V;
    V.vector4_f32[0] = pSource->x;
    V.vector4_f32[1] = pSource->y;
    V.vector4_f32[2] = 0.f;
    V.vector4_f32[3] = 0.f;
    return V;
#elif defined(_XM_ARM_NEON_INTRINSICS_)
    float32x2_t x = vld1_f32(reinterpret_cast<const float*>(pSource));
    float32x2_t zero = vdup_n_f32(0);
    return vcombine_f32(x, zero);
#elif defined(_XM_SSE_INTRINSICS_)
    return _mm_castpd_ps(_mm_load_sd(reinterpret_cast<const double*>(pSource)));
#endif
}

• 可以看到将XMFLOATn转换为XMVECTOR的函数很简单，名为：XMLoadFloatn，参数传入XMFLOATn实例的地址即可。细看函数内部，是通过使用 _mm_castpd_ps 函数实现的类型转换，这函数是SIMD提供的函数。可知DirectXMath不过也只是对SIMD库进行了再一次封装而已。

• 实例代码：

#define _CRT_SECURE_NO_WARNINGS  // 重定向输入输出(否则默认是没有控制台窗口，你也就看不到输出了，此宏必须写在头文件引用之前！)

#include<windows.h>				 // Windows API编程所需头文件
#include<DirectXMath.h>			 // DirectXMath库
#include<iostream>

// Windows API编程的main函数为WinMain，照着写就是了
int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE prevInstance,
	PSTR cmdLine, int showCmd)
{
	// 这三行代码启动一个控制台，让你的cou和cin绑定控制台
	AllocConsole();
	freopen("CONOUT$", "w", stdout);
	freopen("CONIN$", "r", stdin);

	using namespace DirectX;

	XMVECTOR xmvector;
	XMFLOAT2 xmfloat2;
	XMFLOAT3 xmfloat3;
	XMFLOAT4 xmfloat4;

	// 将XMFLOATn转换为XMVECTOR
	xmvector = XMLoadFloat2(&xmfloat2);
	xmvector = XMLoadFloat3(&xmfloat3);
	xmvector = XMLoadFloat4(&xmfloat4);

	while (1); // 阻止程序终止导致控制台关闭无法看到输出信息
	return 0;
}

• 再来学习将XMVECTOR类型转换为XMFLAOTn类型的方法：

inline void XM_CALLCONV XMStoreFloat2
(
    XMFLOAT2* pDestination,
    FXMVECTOR  V
) noexcept
{
    assert(pDestination);
#if defined(_XM_NO_INTRINSICS_)
    pDestination->x = V.vector4_f32[0];
    pDestination->y = V.vector4_f32[1];
#elif defined(_XM_ARM_NEON_INTRINSICS_)
    float32x2_t VL = vget_low_f32(V);
    vst1_f32(reinterpret_cast<float*>(pDestination), VL);
#elif defined(_XM_SSE_INTRINSICS_)
    _mm_store_sd(reinterpret_cast<double*>(pDestination), _mm_castps_pd(V));
#endif
}

• 可以看到将XMVECTOR转换为XMFLOATn类型也是由SIMD的函数 _mm_store_sd 实现的。转换函数名为：XMStoreFloatn。但是参数是两个而且没有返回值，第一个参数是保存结果的XMFLOATn变量的地址，第二个参数是被转换的FXMVECTOR遍历。FXMVECTOR其实就是const XMVECTOR，其类型定义如下：

    typedef const XMVECTOR FXMVECTOR;

• 实例代码：

#define _CRT_SECURE_NO_WARNINGS  // 重定向输入输出(否则默认是没有控制台窗口，你也就看不到输出了，此宏必须写在头文件引用之前！)

#include<windows.h>				 // Windows API编程所需头文件
#include<DirectXMath.h>			 // DirectXMath库
#include<iostream>



// Windows API编程的main函数为WinMain，照着写就是了
int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE prevInstance,
	PSTR cmdLine, int showCmd)
{
	// 这三行代码启动一个控制台，让你的cou和cin绑定控制台
	AllocConsole();
	freopen("CONOUT$", "w", stdout);
	freopen("CONIN$", "r", stdin);

	using namespace DirectX;

	XMVECTOR xmvector = XMVECTOR(); // 试试不显示初始化XMVECTOR会怎么样
	XMFLOAT2 xmfloat2 = XMFLOAT2(1,2);
	XMFLOAT3 xmfloat3;
	XMFLOAT4 xmfloat4;
	
	XMStoreFloat2(&xmfloat2, xmvector);
	std::cout << xmvector.m128_f32[0] << " " << xmvector.m128_f32[1];

	XMStoreFloat3(&xmfloat3, xmvector);
	XMStoreFloat4(&xmfloat4, xmvector);

	while (1); // 阻止程序终止导致控制台关闭无法看到输出信息
	return 0;
}

• 转换XMVECTOR为XMFLOATn选择值返回形式，转换XMFLOATn为XMVECTOR选择无返回值形式，这可能是由于考虑性能而决定的。不同的返回形式转换为汇编代码的数量可能不同，导致性能也就不同。可以看看之前推荐的那篇英文文章，里面介绍了设计SIMD库时需要考虑的代码膨胀。

【2】XMVECTOR获取分量和转换为新XMVECTOR

• 如果我们要获取或设置XMFLAOTn的某个分量，直接.xyz获取或设置即可，但是如果要获取或设置XMVECTOR的某个分量便没有那么容易了。DirectXMath为此提供了专门的函数，获取XMVECTOR某个分量的函数为：

inline float XM_CALLCONV XMVectorGetX(FXMVECTOR V) noexcept
{
#if defined(_XM_NO_INTRINSICS_)
    return V.vector4_f32[0];
#elif defined(_XM_ARM_NEON_INTRINSICS_)
    return vgetq_lane_f32(V, 0);
#elif defined(_XM_SSE_INTRINSICS_)
    return _mm_cvtss_f32(V);
#endif
}

• 函数名为XMVectorGetX，可以看出来也是依靠SIMD的函数实现的，其中可以GetX、Y、Z、W，以此便可获取XMVECTOR的各个分量。
• 根据XMVECTOR变量并设置某个分量创建新的XMVECTOR变量的函数为：

inline XMVECTOR XM_CALLCONV XMVectorSetX(FXMVECTOR V, float x) noexcept
{
#if defined(_XM_NO_INTRINSICS_)
    XMVECTORF32 U = { { {
            x,
            V.vector4_f32[1],
            V.vector4_f32[2],
            V.vector4_f32[3]
        } } };
    return U.v;
#elif defined(_XM_ARM_NEON_INTRINSICS_)
    return vsetq_lane_f32(x, V, 0);
#elif defined(_XM_SSE_INTRINSICS_)
    XMVECTOR vResult = _mm_set_ss(x);
    vResult = _mm_move_ss(V, vResult);
    return vResult;
#endif
}

• 毫无疑问其也是使用SIMD函数实现的，函数名为：XMVectorSetX，当然也可以是SetY、Z和W。要注意的是这个函数的作用是返回一个新的XMVECTOR变量，其值除了被设置的那个分量外都与原XMVECTOR变量相等。
• 实例如下：

#define _CRT_SECURE_NO_WARNINGS  // 重定向输入输出(否则默认是没有控制台窗口，你也就看不到输出了，此宏必须写在头文件引用之前！)

#include<windows.h>				 // Windows API编程所需头文件
#include<DirectXMath.h>			 // DirectXMath库
#include<iostream>



// Windows API编程的main函数为WinMain，照着写就是了
int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE prevInstance,
	PSTR cmdLine, int showCmd)
{
	// 这三行代码启动一个控制台，让你的cou和cin绑定控制台
	AllocConsole();
	freopen("CONOUT$", "w", stdout);
	freopen("CONIN$", "r", stdin);

	using namespace DirectX;

	// 获取XMVECTOR的分量
	XMVECTOR xmvector1 = XMVECTOR();
	std::cout << XMVectorGetX(xmvector1) <<" "
			  << XMVectorGetY(xmvector1) <<" " 
			  << XMVectorGetZ(xmvector1) << std::endl;

	// 设置XMVECTOR的分量
	XMVECTOR xmvector2 =  XMVectorSetX(xmvector1, 1);
	std::cout << XMVectorGetX(xmvector2) << std::endl;

	while (1); // 阻止程序终止导致控制台关闭无法看到输出信息
	return 0;
}

• 运行结果如下：
  
• 可以看到DirectXMath中的核心向量XMVECTOR就是__m128，当然可能会因为硬件的不同而不同。我想说的是DirectXMath就是对SIMD的一次封装而已，基本上向量和矩阵库都要使用SIMD，而对于游戏SIMD几乎是不可或缺。因此我建议大家去学习SIMD相关知识，这样才能了解到问题的本质，这样你才会在使用任何向量和矩阵库时了解到设计的原因。当然这也有利于你在使用XMVECTOR时提高效率，目前SIMD已经支持了最高512位的寄存器和运算，但是DirectXMath还是使用的128位运算，尽管我的CPU支持256位寄存器和运算，它还是如此，因此自己掌握才是真的掌握！SIMD是CPU的指令，因此帮助文档基本上都在各CPU开发商的官网上，Intel SIMD帮助文档，Arm SIMD帮助文档。

（4）参数的传递

• 为了提高运算效率，可以将XMVECTOR类型的值作为函数的参数。直接传送至SSE/SSE2寄存器里，而不存在stack内。以此方式传递的参数数量取决于用户使用的平台（32位windows、64位windows）和编译器。因此为了使代码更具通用性，不受具体平台和编译器的影响，我们利用FXMVECTOR、GXMVECTOR、HXMVECTOR和CXMVECTOR等类型来传递XMVECTOR类型的参数。基于平台和编译器，它们会自动定义为适当的类型。此外，一定要把调用约定注解XM_CALLCONV加在函数名之前，它会根据编译器版本确定出对应的调用约定属性。
• 传递XMVECTOR参数的规则如下：
  &esmp;1. 前三个XMVECTOR参数应当用类型FXMVECTOR。
  &esmp;2. 第四个XMVECTOR参数应当用类型GXMVECTOR。
  &esmp;3. 第5、6个XMVECTOR参数应当用类型HXMVECTOR。
  &esmp;4. 其余的XMVECTOR参数应当用类型CXMVECTOR。
  &esmp;5.