敏感性分析一览

敏感性分析

- Sobol
- Morris
- Fourier Amplitude Sensitivity Test (FAST)
- Random Balance Designs - Fourier Amplitude Sensitivity Test (RBD-FAST)
- Delta Moment-Independent Measure
- Derivative-based Global Sensitivity Measure (DGSM)
- Fractional Factorial Sensitivity Analysis
- High Dimensional Model Representation
- PAWN
- Regional Sensitivity Analysis
- Discrepancy Sensitivity Indices

注：最后两种暂时还没有集成到SALib1.4.7中，需要手动添加官网相关代码。
已手动整理相关代码， 此处跳转。

一个模型有自变量（输入数据）和因变量（输出结果），因变量随自变量的变化而变化，其变化程度与自变量、因变量两者之间关系的强弱决定，敏感性分析便是对强弱关系进行定量讨论，通常将其定量结果称为敏感指数。

敏感指数由三种形式组成。一阶指数衡量单个自变量对因变量方差的贡献；二阶指数衡量两个自变量之间的交互作用对因变量方差的贡献；全阶指数衡量衡量所有自变量（包括一阶效应和其他高阶交互作用）对因变量方差的贡献。

为了方便进行敏感性分析，我们使用Python的敏感性分析库SALib完成计算工作，其包含若干个分析方案，具体如下。

所有方法均以以下相同problem为自变量
定义自变量

problem = {
    'num_vars': 3,
    'names': ['x1', 'x2', 'x3'],
    'bounds': [[-3.14159265359, 3.14159265359],
               [-3.14159265359, 3.14159265359],
               [-3.14159265359, 3.14159265359]]
}

Sobol

# 生成自变量
SALib.sample.sobol.sample(problem: Dict, N: int, *, calc_second_order: bool = True, scramble: bool = True, skip_values: int = 0, seed: int | Generator | None = None)
"""
problem: 自变量定义
N: 样本数量，建议为2的倍数，且不大于skip_values
calc_second_order: 是否需要二阶指数计算，默认为True
scramble: 是否添加干扰，默认为True
skip_values: 需要跳过的序列数目，建议为2的倍数，默认是0
seed: 随机种子
"""

# 敏感分析
SALib.analyze.sobol.analyze(problem, Y, calc_second_order=True, num_resamples=100, conf_level=0.95, print_to_console=False, parallel=False, n_processors=None, keep_resamples=False, seed=None)
"""
problem: 自变量定义
Y: 因变量
calc_second_order: 是否需要二阶指数计算，默认为True
num_resamples: 重采样次数，默认为100
conf_level: 置信区间水平，默认为0.95
print_to_console： 是否输出到操作台，默认为False
parallel: 是否并行分析，默认为False
n_processors: 并行进程数，当parallel=True时使用
keep_resamples: 是否存储中间重采样结果，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
#     'S1': 
#     	array([0.31683154, 0.44376306, 0.01220312]), 
#     'S1_conf': 
#     	array([0.0612548 , 0.05702573, 0.05750855]), 
#     'ST': 
#     	array([0.55586009, 0.44189807, 0.24467539]), 
#     'ST_conf': 
#     	array([0.07651133, 0.04224496, 0.02889387]), 
#     'S2': 
#     	array([[        nan,  0.00925429,  0.23817211],
#        	   [        nan,         nan, -0.0048877 ],
#        	   [        nan,         nan,         nan]]), 
#     'S2_conf': 
#     	array([[       nan, 0.08265217, 0.11277348],
#        	   [       nan,        nan, 0.06331599],
#        	   [       nan,        nan,        nan]])
# }

请添加图片描述

Morris

# 生成自变量
SALib.sample.morris.sample(problem: Dict, N: int, num_levels: int = 4, optimal_trajectories: int = None, local_optimization: bool = True, seed: int = None)
"""
problem: 自变量定义
N: 轨迹数量
num_levels: 网格层数，偶数，默认为4
optimization_trajectories: 要采样的最佳轨迹数量，范围为2到N
local_optimization: 是否使用局部优化，默认为True
seed: 随机种子
"""

# 敏感分析
SALib.analyze.morris.analyze(problem: Dict, X: ndarray, Y: ndarray, num_resamples: int = 100, conf_level: float = 0.95, scaled: bool = False, print_to_console: bool = False, num_levels: int = 4, seed=None)
"""
problem: 自变量定义
X: 自变量
Y: 因变量
calc_second_order: 是否需要二阶指数计算，默认为True
num_resamples: 重采样次数，默认为100
conf_level: 置信区间水平，默认为0.95
print_to_console： 是否输出到操作台，默认为False
parallel: 是否并行分析，默认为False
n_processors: 并行进程数，当parallel=True时使用
keep_resamples: 是否存储中间重采样结果，默认为False
seed: 随机种子
"""

# 结果
print(Si)
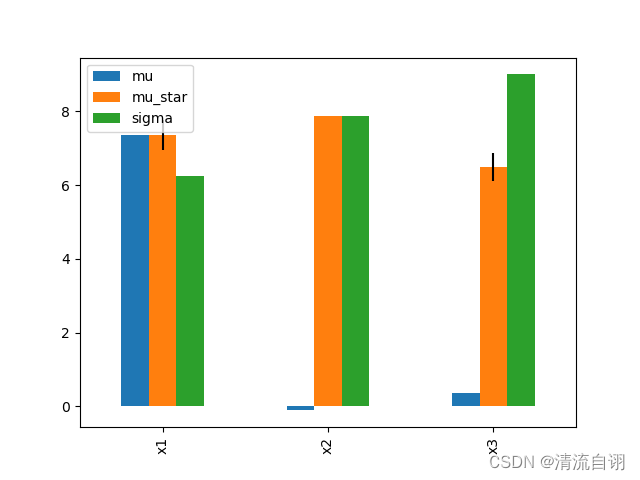
#           mu   mu_star     sigma  mu_star_conf
# x1  7.354122  7.354122  6.242112  3.968815e-01
# x2 -0.110250  7.875000  7.878168  5.248703e-15
# x3  0.362430  6.486250  9.000676  3.725592e-01
# {
#     'names': ['x1', 'x2', 'x3'], 
#     'mu': array([ 7.35412153, -0.11025   ,  0.36243017]), 
#     'mu_star': masked_array(
#         data=[7.354121529806647, 7.875000000000724, 6.4862503552631114],
#         mask=[False, False, False],
#         fill_value=1e+20), 
#     'sigma': array([6.24211213, 7.87816828, 9.000676  ]), 
#     'mu_star_conf': masked_array(
#         data=[0.39688154270651804, 5.248702595241132e-15, 0.37255924946508345],
#         mask=[False, False, False],
#         fill_value=1e+20)
# }

请添加图片描述

Fourier Amplitude Sensitivity Test (FAST)

# 生成自变量
SALib.sample.fast_sampler.sample(problem, N, M=4, seed=None)
"""
problem: 自变量定义
N: 样本数量
M: 干扰参数，默认为4
seed: 随机种子
"""

# 敏感分析
SALib.analyze.fast.analyze(problem, Y, M=4, num_resamples=100, conf_level=0.95, print_to_console=False, seed=None)
"""
problem: 自变量定义
Y: 因变量
M: 干扰参数，默认为4
num_resamples: 重采样次数，默认为100
conf_level: 置信区间水平，默认为0.95
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
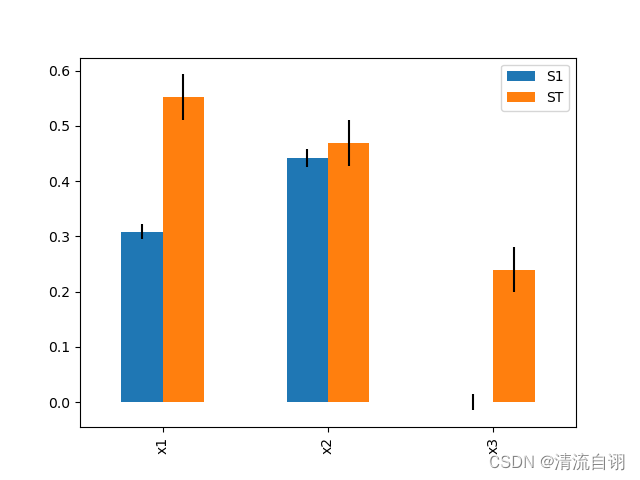
#     'S1': [0.3081232160181247, 0.4420505304594682, 1.0406181235617822e-28], 
#     'ST': [0.5519123814033295, 0.46920370910272835, 0.23930621330436663],
#     'S1_conf': [0.013434507989869757, 0.015813518018138756, 0.015093897483613204], 
#     'ST_conf': [0.041141026199615446, 0.04117206451357777, 0.04071053209490691],
#     'names': ['x1', 'x2', 'x3']
# }

请添加图片描述

Random Balance Designs - Fourier Amplitude Sensitivity Test (RBD-FAST)

# 生成自变量
SALib.sample.latin.sample(problem, N, seed=None)
"""
problem: 自变量定义
N: 样本数量
seed: 随机种子
"""

# 敏感分析
SALib.analyze.rbd_fast.analyze(problem, X, Y, M=10, num_resamples=100, conf_level=0.95, print_to_console=False, seed=None)
"""
problem: 自变量定义
X: 自变量
Y: 因变量
M: 干扰参数，默认为4
num_resamples: 重采样次数，默认为100
conf_level: 置信区间水平，默认为0.95
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
#     'S1': [0.31806056031674595, 0.4450789986938868, 1.5359880927191816e-06],
#     'S1_conf': [0.0556645519811434, 0.07578207765070516, 0.0214559062090626],
#     'names': ['x1', 'x2', 'x3']
# }

请添加图片描述

Delta Moment-Independent Measure

# 敏感分析
SALib.analyze.delta.analyze(problem: Dict, X: ndarray, Y: ndarray, num_resamples: int = 100, conf_level: float = 0.95, print_to_console: bool = False, seed: int = None, y_resamples: int = None, method: str = 'all')
"""
problem: 自变量定义
X: 自变量
Y: 因变量
num_resamples: 重采样次数，默认为100
conf_level: 置信区间水平，默认为0.95
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
y_resamples: 重采样时使用的样本数
method: 计算"delta"、"sobol"或两者"all"，默认为all
"""

# 结果
print(Si)
#        delta  delta_conf        S1   S1_conf
# x1  0.194729    0.021577  0.302742  0.039161
# x2  0.254878    0.022195  0.313650  0.052195
# x3  0.134645    0.020917  0.006901  0.010473
# {
#     'delta': array([0.19472928, 0.25487771, 0.13464494]), 
#     'delta_conf': array([0.02157656, 0.02219531, 0.02091679]), 
#     'S1': array([0.30274202, 0.31365005, 0.00690086]), 
#     'S1_conf': array([0.03916104, 0.0521946 , 0.01047288]), 
#     'names': ['x1', 'x2', 'x3']
# }

请添加图片描述

Derivative-based Global Sensitivity Measure (DGSM)

# 敏感分析
SALib.analyze.dgsm.analyze(problem, X, Y, num_resamples=100, conf_level=0.95, print_to_console=False, seed=None)
"""
problem: 自变量定义
X: 自变量
Y: 因变量
num_resamples: 重采样次数，默认为100
conf_level: 置信区间水平，默认为0.95
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
#     'vi': array([ 7.73312725, 24.37534083, 11.34887321]), 
#     'vi_std': array([16.43522688, 17.35675534, 24.40109617]), 
#     'dgsm': array([2.24329014, 7.07100245, 3.29217592]), 
#     'dgsm_conf': array([1.01703239, 1.0872397 , 1.60391344]), 
#     'names': ['x1', 'x2', 'x3']
# }

请添加图片描述

Fractional Factorial Sensitivity Analysis

# 生成自变量
SALib.sample.ff.sample(problem, seed=None)
"""
problem: 自变量定义
seed: 随机种子
"""

# 敏感分析
SALib.analyze.ff.analyze(problem, X, Y, second_order=False, print_to_console=False, seed=None)
"""
problem: 自变量定义
X: 自变量
Y: 因变量
second_order: 是否需要二阶指数计算，默认为True
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
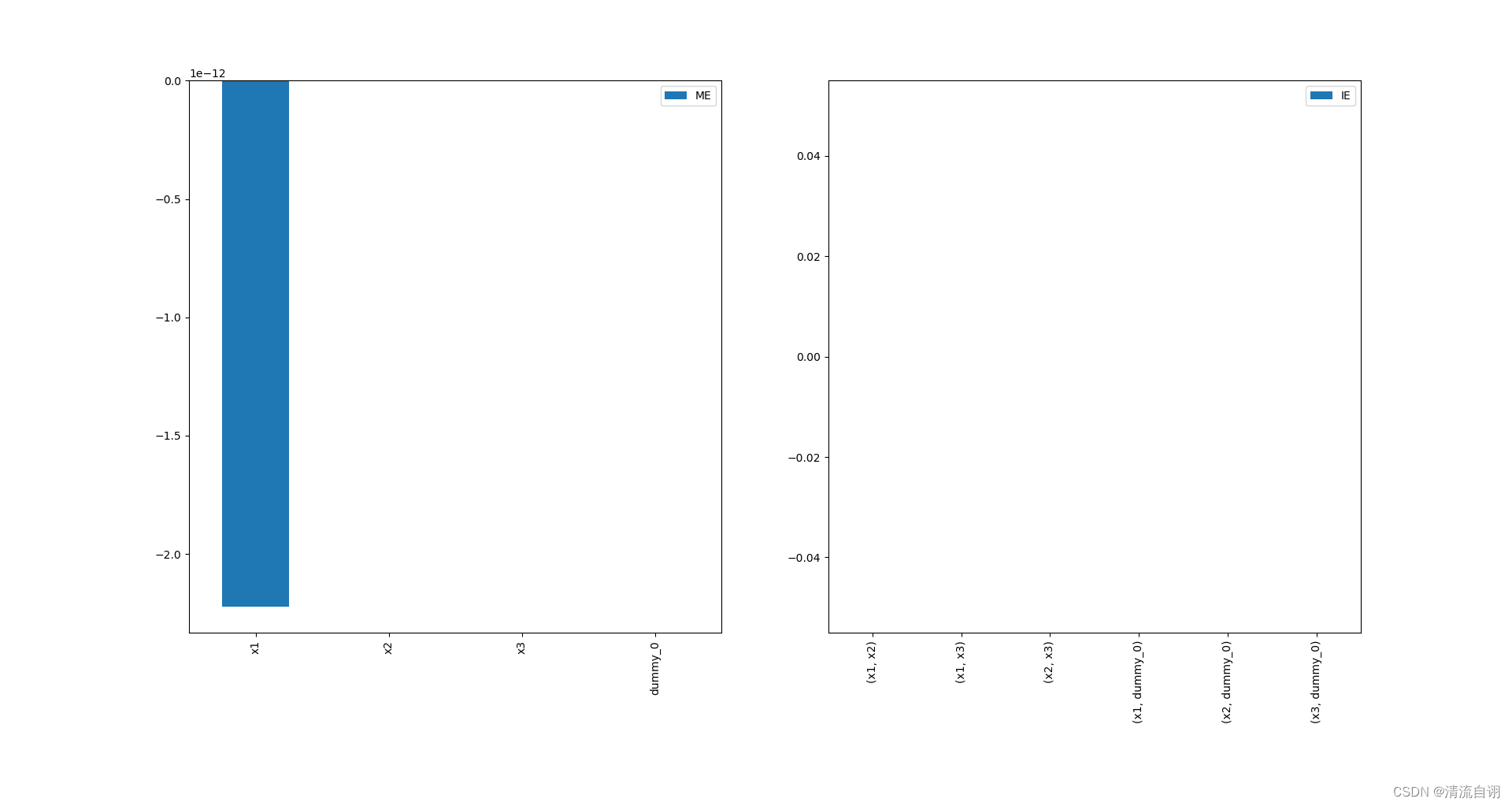
#     'names': ['x1', 'x2', 'x3', 'dummy_0'], 
#     'ME': array([-2.22146819e-12,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00]), 
#     'interaction_names': [('x1', 'x2'), ('x1', 'x3'), ('x2', 'x3'), ('x1', 'dummy_0'), ('x2', 'dummy_0'), ('x3', 'dummy_0')], 
#     'IE': [0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
# }

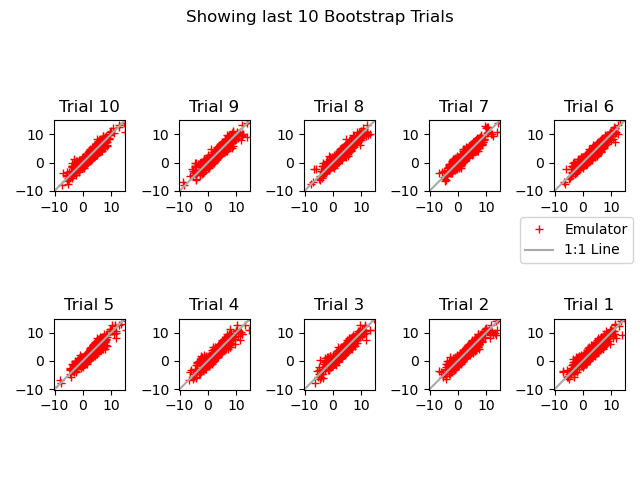
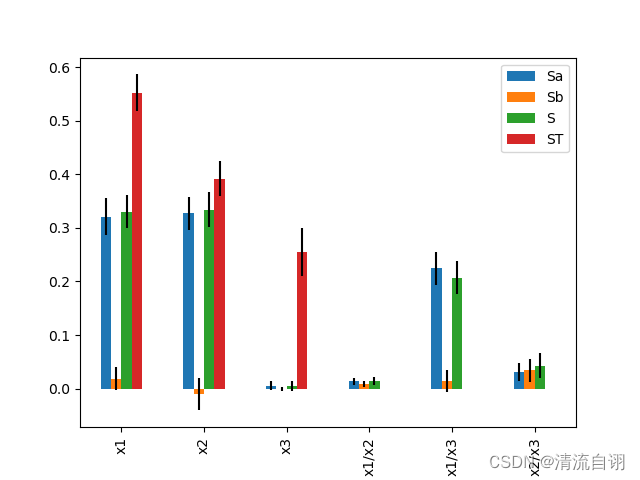
请添加图片描述

High Dimensional Model Representation

# 敏感分析
SALib.analyze.hdmr.analyze(problem: Dict, X: ndarray, Y: ndarray, maxorder: int = 2, maxiter: int = 100, m: int = 2, K: int = 20, R: int = None, alpha: float = 0.95, lambdax: float = 0.01, print_to_console: bool = False, seed: int = None)
"""
problem: 自变量定义
X: 自变量，长度为N
Y: 因变量
maxorder: 最大扩展阶数，范围1-3，默认为2
maxiter: 最大拟合迭代次数，范围1-1000，默认为100
m: B-spline间隔数，范围2-10，默认为2
K: bootstrap迭代次数，范围1-100，默认为20
R: bootstrap样本数，范围100-N/2。默认为N/2，当K为1，R默认为Y的长度
alpha: 置信区间 F 检验，默认为0.95
lambdax: 正则化项，范围0-10，默认0.01
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
#     'Sa': array([0.32098624, 0.32706979, 0.00551071, 0.01372589, 0.22420121,
#        0.03167076]), 
#     'Sa_conf': array([0.03449847, 0.03054272, 0.008012  , 0.00690539, 0.03165136,
#        0.01684393]), 
#     'Sb': array([ 0.01875264, -0.01008509, -0.00085121,  0.00878864,  0.01348094,
#         0.03473462]), 
#     'Sb_conf': array([0.0214207 , 0.03050578, 0.00305786, 0.00632993, 0.02066726,
#        0.02149721]), 
#     'S': array([0.33005615, 0.33421506, 0.00512609, 0.01459155, 0.20722952,
#        0.04286532]), 
#     'S_conf': array([0.03056583, 0.03283559, 0.0086171 , 0.00692596, 0.0308207 ,
#        0.02360502]), 
#     ...............
#     ...............
# }

请添加图片描述

PAWN

# 敏感分析
SALib.analyze.pawn.analyze(problem: Dict, X: ndarray, Y: ndarray, S: int = 10, print_to_console: bool = False, seed: int = None)
"""
problem: 自变量定义
X: 自变量，长度为N
Y: 因变量
S: 调节间隔，默认为10
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
#     'minimum': array([0.172, 0.215, 0.07 ]), 
#     'mean': array([0.2446899 , 0.35838889, 0.12805354]), 
#     'median': array([0.261 , 0.3875, 0.114 ]), 
#     'maximum': array([0.359, 0.489, 0.257]), 
#     'CV': array([0.24174122, 0.26268279, 0.40149537]), 
#     'names': ['x1', 'x2', 'x3']
# }

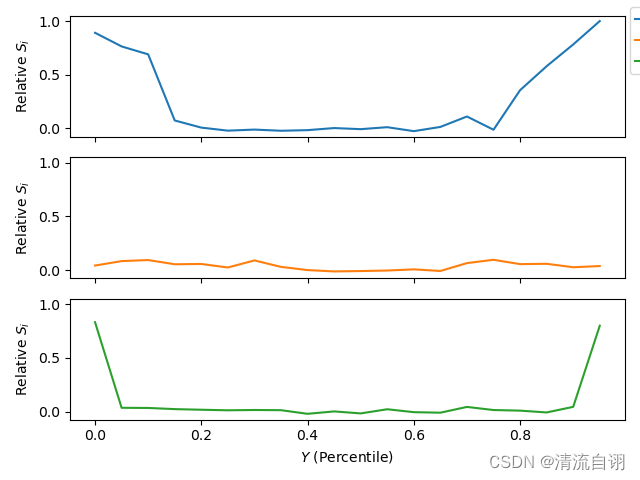
请添加图片描述

Regional Sensitivity Analysis

# 敏感分析
SALib.analyze.rsa.analyze(problem: Dict, X: ndarray, Y: ndarray, bins: int = 20, target: str = 'Y', print_to_console: bool = False, seed: int = None)
"""
problem: 自变量定义
X: 自变量
Y: 因变量
bins: 使用的箱数，默认为20
target: 评估自变量（"X"）或因变量（"Y"），默认为"Y"
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
# 'x1': array([ 0.89094312,  0.76391302,  0.6901172 ,  0.07445683,  0.00810598,
#        -0.02019611, -0.01031206, -0.02119982, -0.01553581,  0.00392679,
#        -0.00631403,  0.01199807, -0.0249512 ,  0.01452995,  0.11153721,
#        -0.01175163,  0.3564372 ,  0.57950908,  0.78215635,  1.        ]), 
# 'x2': array([ 0.04154606,  0.0830033 ,  0.09267739,  0.05356006,  0.05618751,
#         0.02343257,  0.0891207 ,  0.02911934, -0.00066498, -0.01310919,
#        -0.00965545, -0.00484718,  0.00592457, -0.00896379,  0.06430754,
#         0.09513276,  0.05469668,  0.05782315,  0.0256584 ,  0.03686238]), 
# 'x3': array([ 0.83197838,  0.0348991 ,  0.03329039,  0.02259925,  0.01671094,
#         0.01156657,  0.014363  ,  0.01250926, -0.02117361,  0.00110074,
#        -0.01738245,  0.02128902, -0.00589163, -0.01071005,  0.04296997,
#         0.01399239,  0.00837767, -0.00838735,  0.04364362,  0.79882026]), 
# 'names': ['x1', 'x2', 'x3'], 
# 'bins': array([0.  , 0.05, 0.1 , 0.15, 0.2 , 0.25, 0.3 , 0.35, 0.4 , 0.45, 0.5 ,
#        0.55, 0.6 , 0.65, 0.7 , 0.75, 0.8 , 0.85, 0.9 , 0.95]), 
# 'target': 'Y'
# }

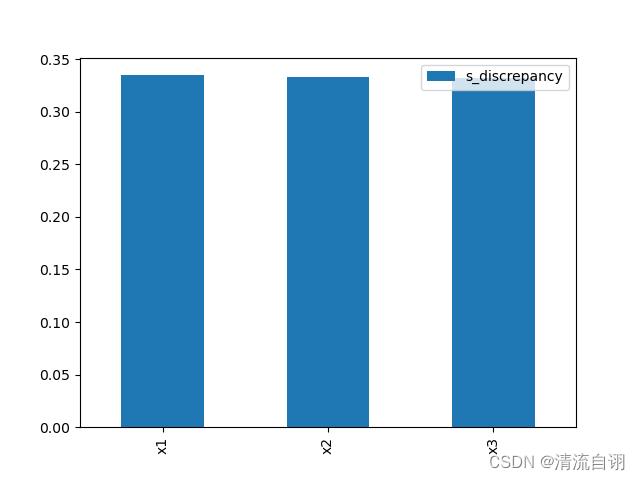
请添加图片描述

Discrepancy Sensitivity Indices

# 敏感分析
SALib.analyze.discrepancy.analyze(problem: Dict, X: ndarray, Y: ndarray, method: str = 'WD', print_to_console: bool = False, seed: int = None)
"""
problem: 自变量定义
X: 自变量
Y: 因变量
method: 差异类型（"WD", "CD", "MD", "L2-star"），默认为"WD"。
print_to_console： 是否输出到操作台，默认为False
seed: 随机种子
"""

# 结果
print(Si)
# {
# 's_discrepancy': array([0.33467611, 0.33305819, 0.3322657 ]), 
# 'names': ['x1', 'x2', 'x3']
# }

请添加图片描述

敏感性分析一览

敏感性分析

Sobol

Morris

Fourier Amplitude Sensitivity Test (FAST)

Random Balance Designs - Fourier Amplitude Sensitivity Test (RBD-FAST)

Delta Moment-Independent Measure

Derivative-based Global Sensitivity Measure (DGSM)

Fractional Factorial Sensitivity Analysis

High Dimensional Model Representation

PAWN

Regional Sensitivity Analysis

Discrepancy Sensitivity Indices

相关文章

Flutter笔记：滚动之-无限滚动与动态加载的实现（GetX简单状态管理版）

Spring Framework 学习笔记5：事务

云原生Kubernetes：对外服务之 Ingress

Python海洋专题五之水深地形图海岸填充

怒刷LeetCode的第21天（Java版）

JUC第十二讲：JUC锁: 锁核心类AQS详解

aarch64 平台 musl gcc 工具链手动编译方法

【算法训练-贪心算法】一买卖股票的最佳时机II

开源校园服务小程序源码校园综合服务小程序源码包含快递代取打印服务校园跑腿【带详细部署教程】

【python海洋专题一】查看数据nc文件的属性并输出属性到txt文件

【JavaScript】读取本地json文件并绘制表格

八、垃圾收集高级

【每日一题】1498. 满足条件的子序列数目

buuctf-[WUSTCTF2020]CV Maker

设计模式7、桥接模式 Bridge

安卓 kuaishou 设备did和egid 学习分析

c#设计模式-结构型模式之装饰者模式

优化用户体验：解决element中el-tabs组件切换闪屏问题

LeetCode面向运气之Javascript—第58题-最后一个单词的长度-99.83%

力扣 -- 97. 交错字符串