A 收集元素的最少操作次数
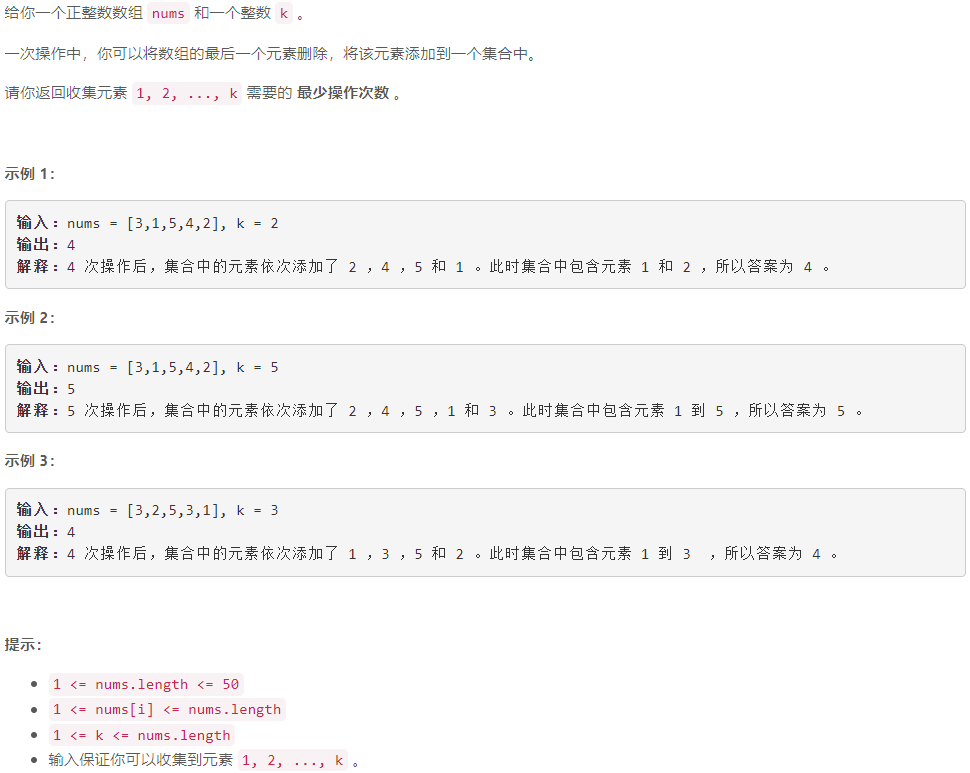
模拟: 反序遍历数组,用一个集合存当前遍历过的不超过 k k k 的正数
class Solution {
public:
int minOperations(vector<int> &nums, int k) {
unordered_set<int> vis;
int n = nums.size();
int i = n - 1;
for (;; i--) {
if (nums[i] <= k && !vis.count(nums[i]))
vis.insert(nums[i]);
if (vis.size() == k)
break;
}
return n - i;
}
};
B 使数组为空的最少操作次数
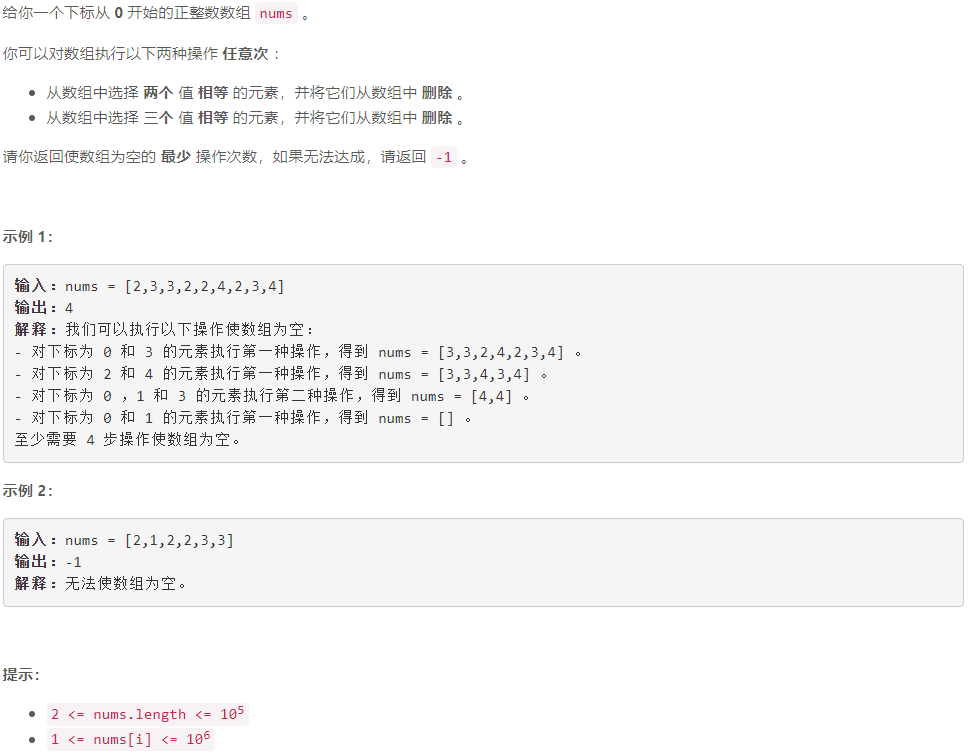
计数:记录数组中各元素出现次数,若存在只出现一次的元素则无法使数组为空,否则,要将出现次数为 f f f 的某个元素全部删除最少需要的次数为:当 f % 3 = 0 f\%3=0 f%3=0 时为 f 3 \frac f 3 3f ,当 f % 3 ≠ 0 f\%3\ne 0 f%3=0 时为 ⌊ f 3 ⌋ + 1 \left \lfloor \frac f 3 \right \rfloor + 1 ⌊3f⌋+1 。
class Solution {
public:
int minOperations(vector<int> &nums) {
unordered_map<int, int> cnt;
for (auto x: nums)
cnt[x]++;
int res = 0;
for (auto [_, f]: cnt) {
if (f == 1)
return -1;
if (f % 3 == 0)
res += f / 3;
else
res += f / 3 + 1;
}
return res;
}
};
C 将数组分割成最多数目的子数组
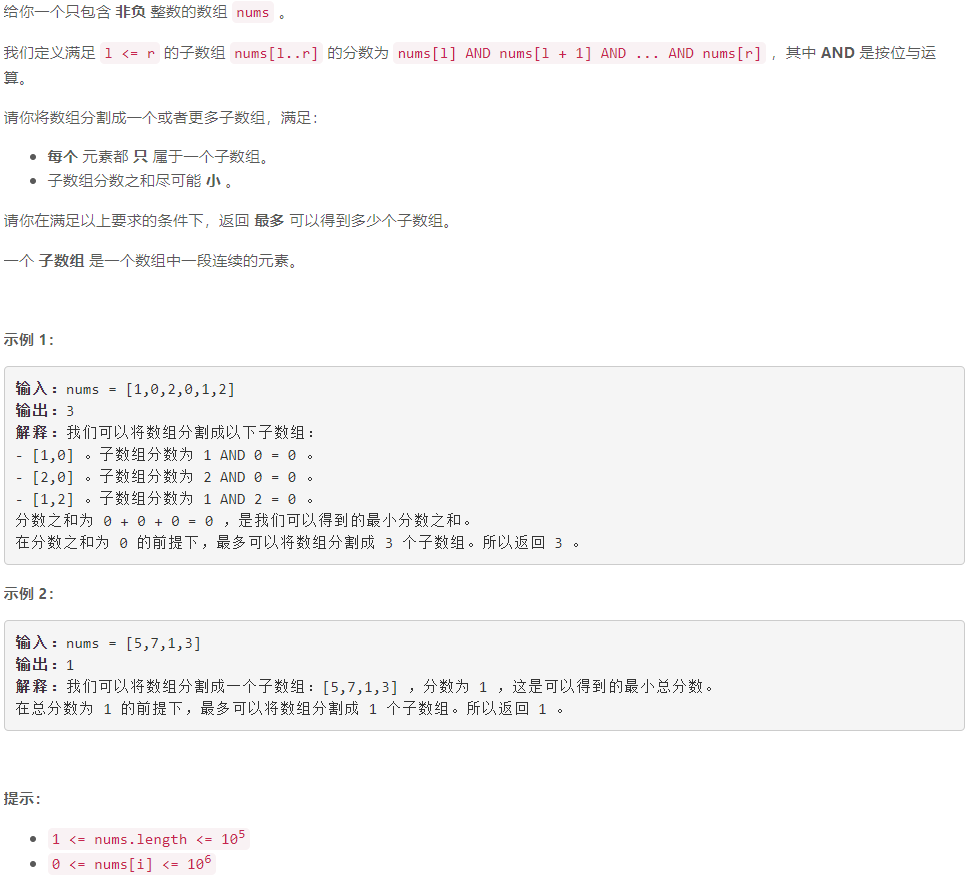
模拟:遍历数组元素 n u m s [ i ] nums[i] nums[i] ,若 n u m s [ i ] nums[i] nums[i] 不是最后一个元素,则只有一种情况会使得最优解中 n u m s [ i ] nums[i] nums[i] 为其所在子数组的最后一个元素: n u m s [ i ] nums[i] nums[i] 所在的子数组分数已经为 0 0 0 且 n u m s [ i + 1 ] & ⋯ & n u m s [ n u m s . s i z e ( ) − 1 ] nums[i+1]\&\cdots\&nums[nums.size()-1] nums[i+1]&⋯&nums[nums.size()−1] 等于 0 0 0
class Solution {
public:
int maxSubarrays(vector<int> &nums) {
int n = nums.size();
vector<int> sf(n);//“后缀与”数组
sf[n - 1] = nums[n - 1];
for (int i = n - 2; i >= 0; i--)
sf[i] = nums[i] & sf[i + 1];
int res = 0;
for (int i = 0, cur = nums[0]; i < n; i++) {
cur &= nums[i];
if (i == n - 1 || cur == 0 && sf[i + 1] == 0) {//nums[i]为所在子数组的最后一个元素
res++;
if (i != n - 1)
cur = nums[i + 1];//下一个子数组的首个元素
}
}
return res;
}
};
D 可以被 K 整除连通块的最大数目
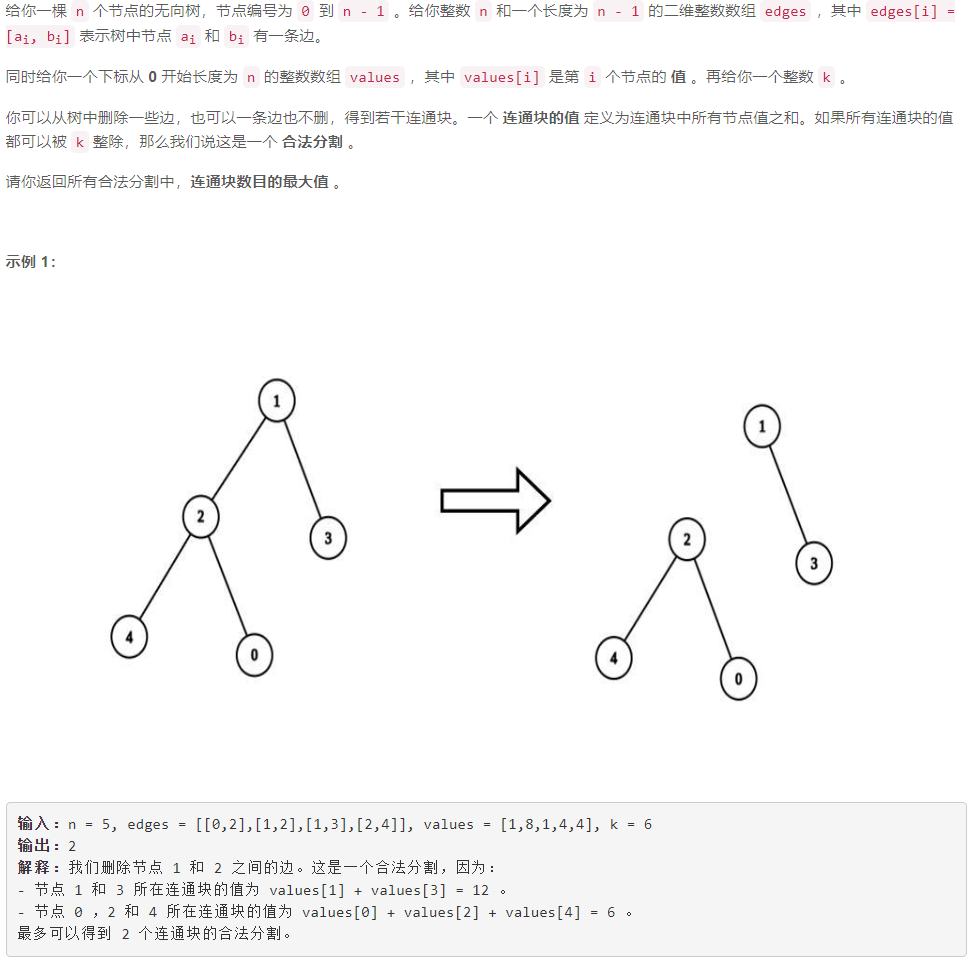
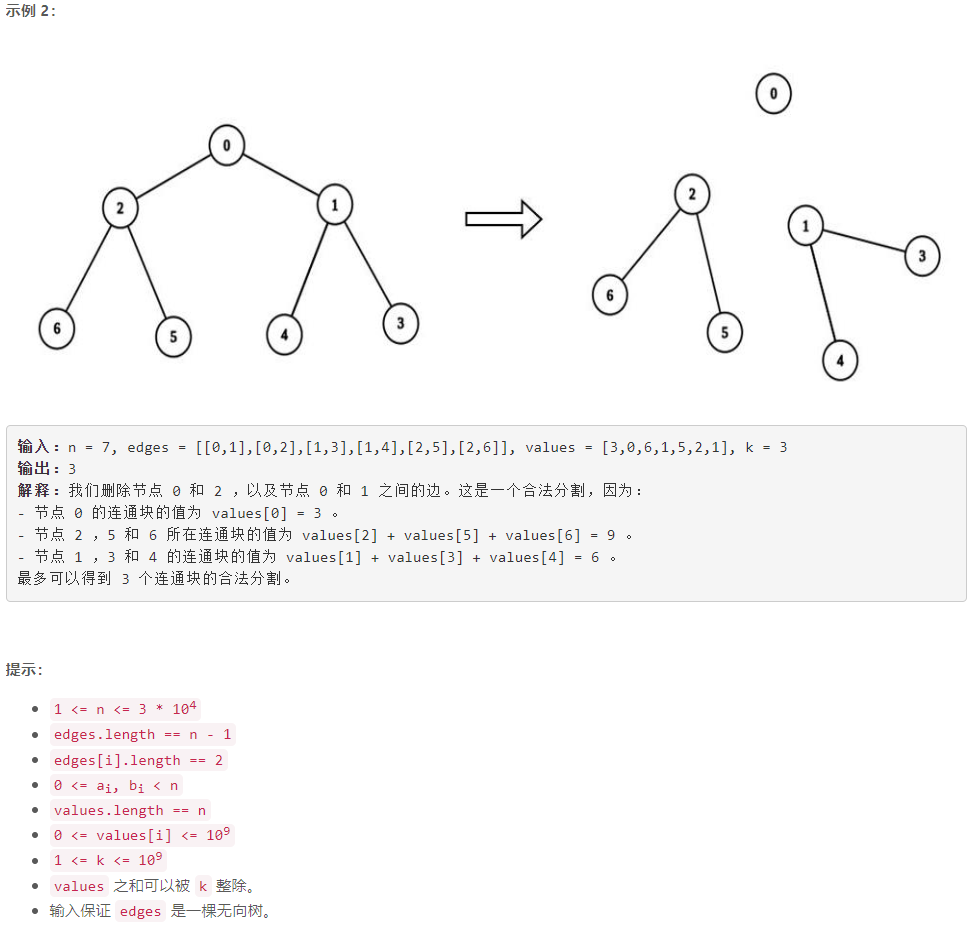
d f s dfs dfs:不妨以 0 0 0 为树根,通过 d f s dfs dfs 求 s s s 数组: s [ i ] s[i] s[i] 为以 i i i 为根的子树的所有节点值之和。设 d f s dfs dfs 遍历到的当前节点为 c u r cur cur ,若遍历到 c u r cur cur 的子节点 j j j 时,有 s [ j ] % k = = 0 s[j]\%k==0 s[j]%k==0 ,则边 ( c u r , j ) (cur,j) (cur,j) 可以删除(即可以增加一个连通块)。
class Solution {
public:
using ll = long long;
int maxKDivisibleComponents(int n, vector<vector<int>> &edges, vector<int> &values, int k) {
vector<int> e[n];//邻接表
for (auto &ei: edges) {//建图
e[ei[0]].push_back(ei[1]);
e[ei[1]].push_back(ei[0]);
}
vector<ll> s(n);
int res = 1;
function<ll(int, int)> dfs = [&](int cur, int par) {//当前节点为cur,父节点为par
s[cur] += values[cur];
for (auto j: e[cur])
if (j != par) {
s[cur] += dfs(j, cur);
if (s[j] % k == 0)
res++;
}
return s[cur];
};
dfs(0, -1);//以0为根跑dfs
return res;
}
};