数据结构–栈的实现
1.栈的概念和结构:
栈的概念:栈是一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端
称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
栈的应用:栈其实可以看作一个弹夹,数据就是一个一个的子弹,而子弹在弹夹中确是先进去的要后被发射,最后后进去的反而会先被发射。**进栈就是装子弹的过程,而出栈就是发射子弹的过程。**同时,向栈中插入数据的操作也被称作压栈、进栈、入栈等。取出栈中数据的的操作则被称之为出栈、弹栈。

栈的结构:
下图是向栈中插入数据(Top),只能从栈顶插入数据。

下图是取出栈中的数据(Pop),只能从栈顶取出数据。
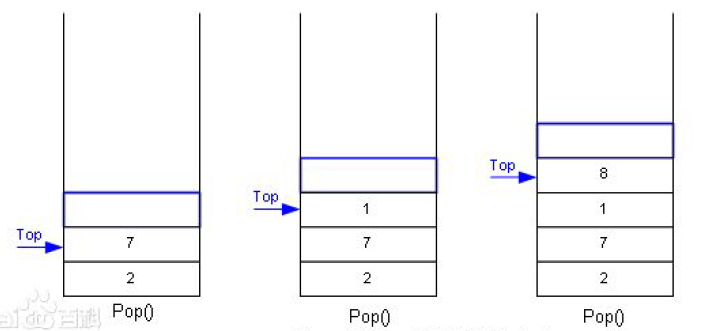
1.1进出栈的变化形式
- 请问现在向栈中顺序插入了1,2,3这三个数据的出栈顺序是不是就是3,2,1呢?
其实这个出栈的顺序和入栈的顺序有很大的关系.比如先向栈入插入了1和2,然后将这两个取出来,那么取出的顺序就是2,1,接着将3插入栈中,接着就取出3,那么所有元素的出栈的顺序就是2,1,3,这与入栈元素的个数和出栈的情况有关. - 先入栈的元素是不是就只能最后出栈呢??
答案也是不一定的,举个例子:现在有1,2,3这三个元素,向栈中先插入1和2,接着将这两个元素取出,那么取出的顺序就是2和1,接着将3入栈,然后将3取出来,此时对于整个栈来讲,最先进栈的是1,而最后出栈的则是3. - 此时还是有1,2,3这三个元素,请问有没有一种特定的插入栈顺序(保证1,2,3是按顺序进栈),使得这些元素按照3,1,2(3最先出栈)的顺序出栈呢??
答案是没有的,无论如何都不可能是3,1,2这样的顺序出栈.因为要想第一个出3,那么肯定需要将1,2,3按次序都插入栈中,将3取出之后,接着栈顶的元素是2,要想取到1,必须先取出2.那么显然是不可能先取出1的.
2.栈的实现
栈的特点:
由于栈拥有顺序表的特点,但是由于栈的特殊性,所以针对栈在操作上会有变化,特别是插入和删除操作分别称作push和pop,英文翻译分别是压和弹,更方便理解.当作是对子弹进行操作就比较好记忆了.
实现方式:
栈的实现可以采用链表和数组两种方式,但是使用数组更方便,用数组对栈进行删除和插入操作时,只需要对数组的下标进行操作即可,代价较小,但是使用链表还需要进行释放节点,新建节点等操作,成本高.
栈中存储的数据可以使用typedef来定义,这样就可以做到自由更改栈中的数据类型.
那么针对的栈的特有的操作有哪些呢 ??
// 初始化栈
void StackInit(Stack* ps);
// 入栈
void StackPush(Stack* ps, STDataType data);
// 出栈
void StackPop(Stack* ps);
// 获取栈顶元素
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数
int StackSize(Stack* ps);
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(Stack* ps);
// 销毁栈
void StackDestroy(Stack* ps);
针对栈这种只能支持在一端进行插入和删除操作的特殊结构,采用数组的0下标处作为栈底是比较好的,因为首元素都在栈底,变化最小.我们使用一个top指针来指向栈顶的元素,也就是在top变量中存储栈顶元素在数组中的下标.
top指针就相当于游标卡尺上的游标,游标来回移动就代表中栈顶元素的插入和删除,当游标到了最大容量时,也就是栈满了的时候,就需要扩容了,所以需要一个capacity变量用于记录栈的最大容量,容量满了之后就用realloc函数进行扩容,为数组动态开辟空间.所以栈的定义如下:
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int Capacity;//容量
int top;//栈顶指针
}Stack;
但是当一开始栈中没有元素时,top的值该设置为多少呢??假如top的初始值是0,想象在坐标-1处有一个元素,那么此时的top相当于就是指向了栈顶元素的下一个位置.假定top的初始值为-1,就说明top指向的是栈顶元素.本文采用的是前者这种方式.
2.1初始化栈
这里首先将栈的容量设置为0.
void StackInit(Stack* ps)
{
assert(ps);
ps->a = NULL;
ps->Capacity = 0;
ps->top = 0;//top的值为0则说明指向栈顶的下一个元素
}
2.2向栈中插入数据
向栈中插入数据是push(压)操作,注意:插入之前要注意检查栈的容量是否已经满了.并且向栈中插入数据之后,top一定要自增1.因为本文这里top永远保存的是栈顶元素的下一个位置.
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
//先检查容量
if (ps->top == ps->Capacity)
{
int newCapacity = ps->Capacity == 0 ? 4 : ps->Capacity * 2;
ps->Capacity = newCapacity;
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType)*newCapacity);
if (tmp == NULL)
{
perror("realloc fail:");
exit(-1);
}
ps->a = tmp;
}
ps->a[ps->top] = data;
ps->top++;
}
2.3获取栈顶数据
获取栈顶数据之前,要检查top是否为0.为0则说明栈已经为空,没有数据了,由于top存储的是栈顶元素的下一个位置,所以返回的值是top-1位置处的值.
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->top);
return ps->a[(ps->top)-1];
}
2.4删除栈顶数据
删除栈顶数据之前,要检查top是否为0.为0则说明栈已经为空,没有数据了,同时只需要将top–即可,因为top指向的栈顶元素的下一个位置,相当于此时就把栈顶元素等效删除了.
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->top);//防止元素个数为0
(ps->top)--;//让栈顶指针后移
}
2.5销毁栈
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->a);
ps->Capacity = ps->top = 0;
ps = NULL;
}
2.6获取栈中有效元素的个数
既然top指向的是栈顶元素的下一个位置的下标,那么top的值刚好就是栈中的元素的个数.
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->top;
}
2.7检测栈是否为空
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(Stack* ps)
{
assert(ps);
return (ps->top) == 0;
}
3.栈的作用
有的小伙伴可能会想,可以直接使用数组或链表实现这些功能即可.为什么还需要单独设计出来这个栈的数据结构呢?其实,栈的引入简化了程序设计问题,划分了不同层次,使得思考范围缩小,更加聚焦于我们要解决的问题的核心,反之,像数组等,需要我们分散精力取考虑元素的下标的增减问题等问题,反而掩盖了问题的本质.
4.结束
栈就讲到这里啦,欢迎各位小伙伴在评论区中指正本文的不足.下期见!