Tag

【贪心】【排序】【数组】【2023-09-30】

---

题目来源

2136. 全部开花的最早一天

---

题目解读

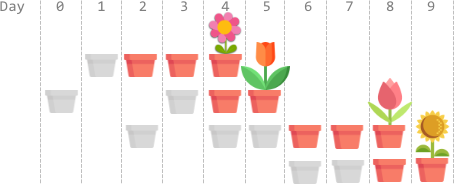
每一朵花需要先种下种子才会生长、开花。种种子需要花一些时间，生长也需要一些时间。每天只能种一颗种子，你可以连续几天都在种一颗种子也可以不连续种植。种子在生长的最后一天之后会一直开放。请计算所有种子都开花的最早一天。

---

解题思路

方法一：贪心+排序

参考 贪心及其证明（Python/Java/C++/Go/JS/Rust） 写的自己的理解。

需要交替播种吗？

播种很多的种子，总的播种时间是不会变的，等于所有种子的播种时间之和。对比播种完成一颗种子再去播种下一刻种子与交替播种种子这两种情况，交替播种种子会导致某些种子的播种完成时间延后，这对开花时间可能会造成延后的影响（没有好处），因此不考虑交替播种种子，应该播种玩一颗种子再去播种另一颗种子。

谁先播种？

我们先看局部最优的情况，即播种两颗种子不同播种顺序下的最早开花时间。

为了便于叙述，设两颗种子播放的所需天数为 p1 和 p2，生长所需天数为 g1 和 g2。不妨设 g1 >= g2，我们来计算一下不同播种顺序下的最晚开花时间：

• 先播种种子 1 再播种种子 2：最晚开花时间为 max(p1 + g1, p1 + p2 + g2)；
• 先播种种子 2 再播种种子 1：最晚开花时间为 max(p1 + p2 + g1, p2 + g2)；

接下来，比较一下以上两种播种顺序下的最晚开花时间。因为 g1 >= g2，且 p1 > 0，所以 max(p1 + p2 + g1, p2 + g2) = p1 + p2 + g1。因为 p1 + g1 < p1 + p2 + g1，且 p1 + p2 + g2 <= p1 + p2 + g1，所以 max(p1 + g1, p1 + p2 + g2) <= p1 + p2 + g1，于是有：max(p1 + g1, p1 + p2 + g2) <= max(p1 + p2 + g1, p2 + g2)。

上式表明，按照 “先播种种子 1 再播种种子 2” 的顺序播种，最晚开花时间不会晚于 “先播种种子 2 再播种种子 1” 的播种顺序的最晚开花时间。

局部最优的方案是：让生长天数大的种子先播放。

以上局部最优的方案意味着 按照生长天数从大到小排序 后，交换任意两颗种子的播种顺序，不会让最晚开花时间提前。

接下来用反证法证明以上局部最优的方案是全局最优的。反证法只需要找出一个反例即可证明反证法假设不成立。

假设存在其它更优的种子排列，我们可以交换「生长天数小且排在前面的种子」与「生长天数大且排在后面的种子」，从而得到更早的最晚开花时间（这又是一个更优的种子播种方案了，与当前假设的最优方案不符），因此假设不成立，故 按照生长天数从大到小的顺序播种 也是全局最优的。

实现代码

class Solution {
public:
    int earliestFullBloom(vector<int>& plantTime, vector<int>& growTime) {
        int n = plantTime.size();
        vector<int> id(n);
        iota(id.begin(), id.end(), 0);
        sort(id.begin(), id.end(), [&](int i, int j) {
            return growTime[i] > growTime[j];
        });
        int res = 0, days = 0;
        for (auto i : id) {
            days += plantTime[i];
            res = max(res, days + growTime[i]);
        }
        return res;
    }
};

复杂度分析

时间复杂度：$O(nlogn)$，$n$ 是数组 plantTime 的长度。

空间复杂度：$O(n)$，使用的额外变量为排序使用的辅助数组 id。

---

写在最后

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出 💬💬💬。

如果大家有更优的时间、空间复杂度方法，欢迎评论区交流。

最后，感谢您的阅读，如果感到有所收获的话可以给博主点一个 👍 哦。