堆结构、堆排序
堆结构的实现
- 堆结构就是用数组实现的完全二叉树结构
2)完全二叉树中如果每颗子树的最大值都在顶部就是大根堆
3)完全二叉树中如果每颗子树的最小值都在顶部就是小根堆
4)堆结构的向上调整和向下调整算法
向上调整
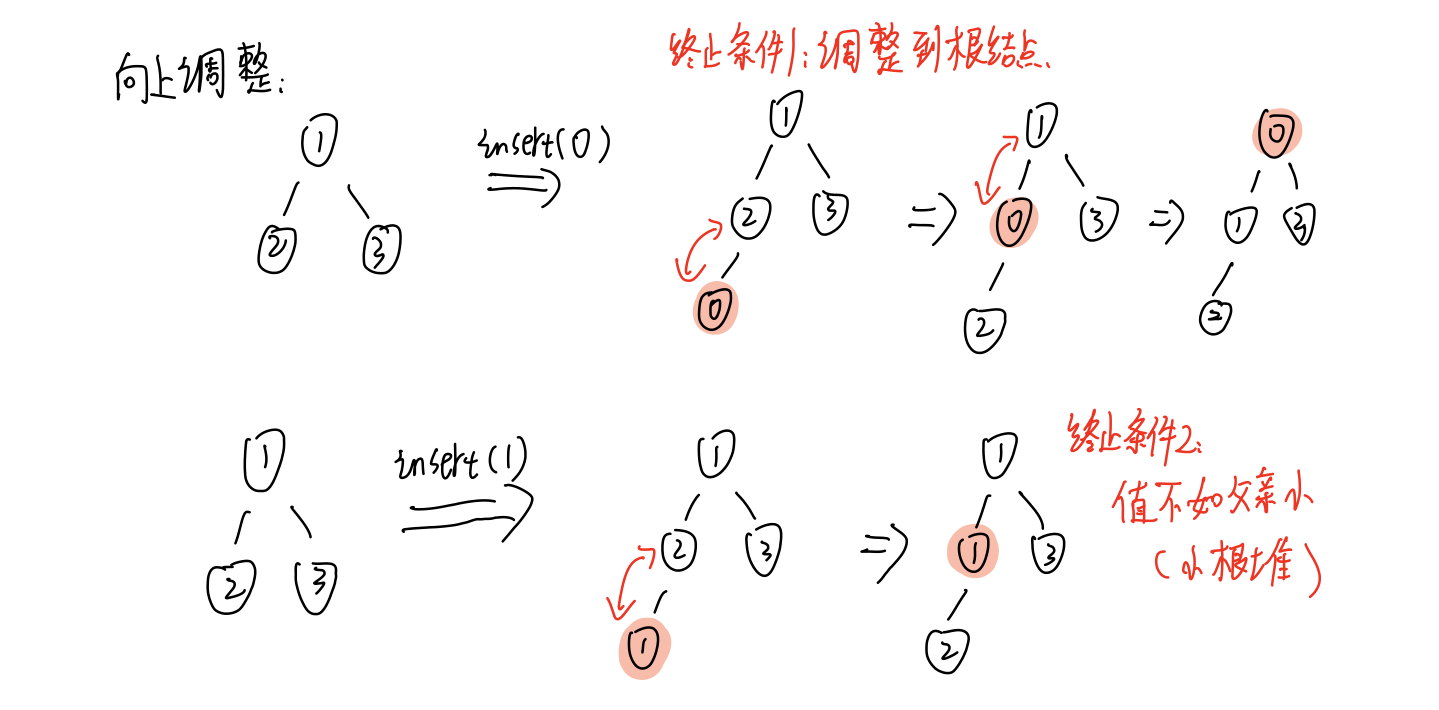
向下调整

5)堆结构某个元素的增大和减少
6)优先级队列结构就是堆结构
空树是完全二叉树,完全二叉树的性质:
如果父亲下标为i : 左孩子:2*i+1 右孩子: 2*i+2
如果孩子下标为i: 父亲的下标:(i-1)/2
#pragma once
#include<iostream>
#include<algorithm>
using namespace std;
template<class T>
//大堆结构
class Heap
{
public:
//构造函数
Heap()
:_a(nullptr)
,_size(0)
,_capacity(0)
{
}
int size()
{
return _size;
}
int empty()
{
return _size == 0;
}
//返回堆顶元素
T& top()
{
return _a[0];
}
//析构函数
~Heap()
{
free(_a);
_a = nullptr;
_size = _capacity = 0;
}
//打印堆中的元素
void Print()
{
for (int i = 0; i < _size; i++)
{
cout << _a[i] << " ";
}
}
//向下调整算法
//从parent位置向下调整
void AdjustDown(int parent)
{
//何时调整结束:调整到叶子节点 或者 父亲节点的值大于(小于)孩子节点
int child = parent * 2 + 1;//默认较大的是左孩子
while (child < _size)
{
//选出较大的孩子
//防止没有右孩子导致越界
if (child + 1 < _size && _a[child] < _a[child + 1])
{
++child;//右孩子更大
}
//判断是否需要交换
if (_a[child] < _a[parent])
{
swap(_a[child], _a[parent]);//父亲和孩子交换
parent = child;//迭代往下调整, 父亲到达孩子的位置
child = parent * 2 + 1;//重新计算孩子的下标
}
else
{
break;
}
}
}
//向上调整算法
//从child位置向上调整
void AdjustUp(int child)
{
//何时调整结束:调整到根节点 或者 孩子节点的值大于(小于)父亲节点
//当child = 0,可以跳出循环
//或者孩子节点的值<父亲节点的值可以跳出循环
while (_a[child] > _a[(child - 1) / 2])
{
swap(_a[child], _a[(child - 1) / 2]);
child = (child - 1) / 2;//孩子调整到父亲位置
}
}
//弹出堆顶元素
void HeadPop()
{
//堆顶元素和最后一个元素交换,然后堆中元素个数--,再从堆顶向下调整
swap(_a[0], _a[_size]);
_size--;
AdjustDown(0);//从0位置开始向下调整
}
//检查容量
void CheakCapacity()
{
//插入到_size位置,要检查容量
if (_size == _capacity)
{
//扩容
int newcapacity = _capacity == 0 ? 4 : _capacity * 2;
T* tmp = new T[newcapacity];//开辟newcapacity个空间,元素类型是T
//把原来的数据插入到新空间
for (int i = 0; i < _size; i++)
{
tmp[i] = _a[i];
}
delete[] _a;//释放旧空间
_a = tmp;//_a指向新空间
_capacity = newcapacity;//更新容量
}
}
//插入元素到_size位置
void HeapInsert(T val)
{
CheakCapacity();
_a[_size] = val;//插入到_size位置
_size++;//堆中元素个数++
AdjustUp(_size-1);//从_size-1位置向下调整
}
private:
T* _a;
int _size;//堆中元素个数
int _capacity;//容量
};
堆排序的实现
1.先让整个数组都变成大根堆结构,建立堆的过程:
1)从上到下的方法: 时间复杂度:O(N*logN)
2)从下到上的方法:时间复杂度:O(N)
2.把堆顶数据和堆尾数据交换,然后减少堆的大小,再去调堆,一直周而复始,时间复杂度:O(N*logN)
3.堆的大小减小成0之后,排序完成
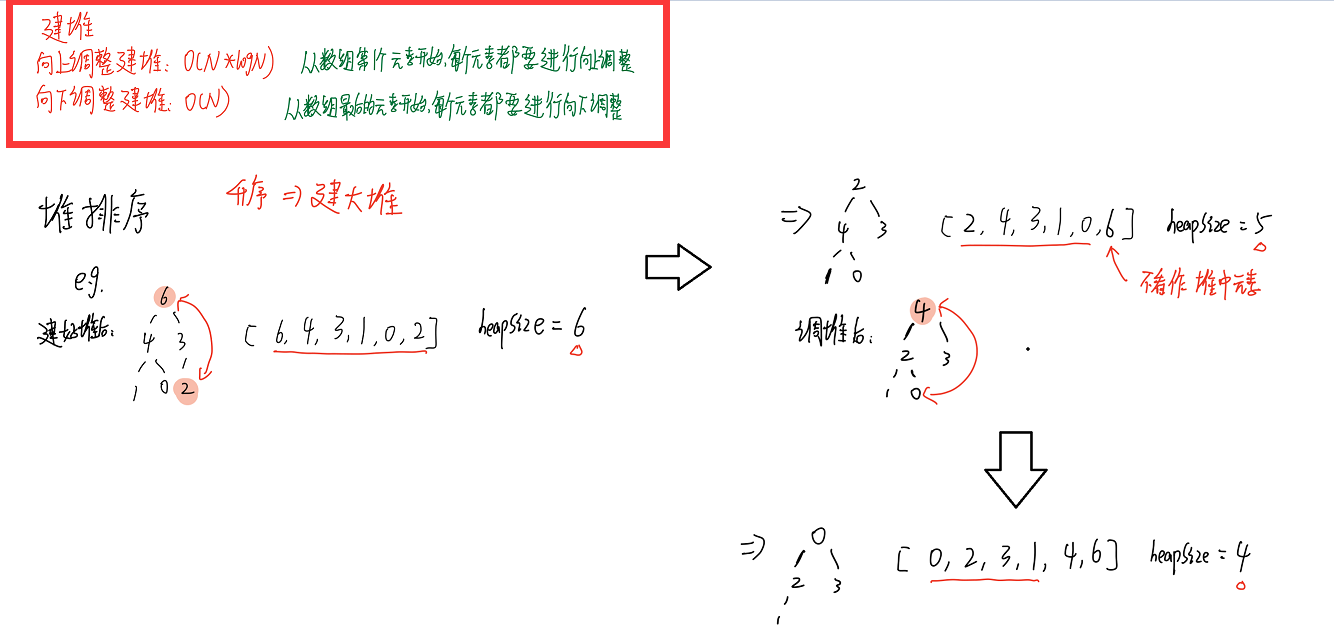
//向上调整
void heapInsert(int* a, int index)
{
while (a[index] > a[(index - 1) / 2]) {
swap(a[index], a[(index - 1) / 2]);
index = (index - 1) / 2;
}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;//默认是左孩子
while (child < n)
{
//如果有右孩子且右孩子的值>左孩子则child变成右孩子,选出较大的孩子
if (child + 1 < n && a[child + 1] > a[child])
{
child += 1;
}
//如果大的孩子的值比父亲大,则交换,迭代继续往下调整
//parent的下标比child下标的值小,往下调整,parent下标变大,即要把child的下标赋给parent,然后再迭代找孩子比较
if (a[child] > a[parent])
{
swap(a[child], a[parent]);
//迭代
parent = child;//切记这里是把孩子的下标给父亲,不要和向上调整弄混
child = parent * 2 + 1;
}
//大的孩子的值比父亲的值小,不用调整了
else
{
break;
}
}
}
void heapSort(int* a, int n)
{
if (a == nullptr || n < 2)
{
return;
}
//1.建堆
//方法1:向上调整建堆:O(N*logN)
/*for (int i = 0; i < n; i++)
{
heapInsert(a, i);
}*/
//方法2:向下调整建堆
//从 数组的最后一个元素开始调整
for (int i = n - 1; i >= 0; i--)
{
AdjustDown(a, n, i);//从i位置开始向下调整,共有n个元素
}
int heapsize = n;//堆中元素个数
//堆顶和堆尾元素交换,然后堆中元素减少一个
swap(a[0], a[--heapsize]);
//每个数都需要调堆,直到堆元素个数为0
while (heapsize > 0)
{
AdjustDown(a, heapsize,0);//O(N*logN) //从0位置开始向下调整,共heapsize个元素
swap(a[0], a[--heapsize]);//堆顶和堆尾元素交换,然后堆中元素减少一个
}
}
题目:数组每个元素移动k步排好序
已知一个几乎有序的数组。几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离一定不超过k, k相对于数组长度来说是比较小的。请选择一个合适的排序策略,对这个数组进行排序。
首先:整个数组的最小值肯定是在 位置0~位置k这个范围里的,这K+1个数组成一个小根堆,这个小根堆的堆顶肯定是整个数组的最小值,把堆顶元素弹出放在数组的 位置0 上
然后再加入一个数,第二小的数肯定在原来的位置1~位置k+1的范围上…

加一个数弹一个数,最后没得加了,就依次弹出堆顶数据
一共弹出N个数,小根堆只有K个数,调堆高度为:logK
所以时间复杂度: O(N*logK) 如果K比较小 时间复杂度O(N)
空间复杂度:K+1 堆中元素不超过k+1个
#include<vector>
#include<queue>
#include<functional>
void sortedArrDistanceLessK(vector<int> v, int k)
{
if (k == 0)//说明已经有序
{
return;
}
//准备一个小根堆
priority_queue<int, vector<int>, greater<int>> q;
//创建k个数的小根堆
int index = 0; //0->k-1
//注意:有可能数组元素不够k个
int n = v.size() > k ? k : v.size() ;
for (index = 0; index < n; index++)
{
q.push(v[index]);//把前k个数进堆
}
int i = 0;
//依次从原数组加入数据到堆中 和 弹出数据放到原数组
for (; index < v.size(); index++)
{
q.push(v[index]);//加入数据
//弹出数据放到原数组
v[i++] = q.top();
q.pop();
}
//最后没得加了,就依次弹出堆中数据,放到原数组
while (!q.empty())
{
v[i++] = q.top();
q.pop();
}
}
和堆有关的面试题、加强堆结构
线段最大重合问题
题目:
给定很多线段,每个线段都有两个数[start, end],
表示线段开始位置和结束位置,左右都是闭区间
规定:
1)线段的开始和结束位置一定都是整数值
2)线段重合区域的长度必须>=1
返回线段最多重合区域中,包含了几条线段
方法1:枚举
方法1:枚举

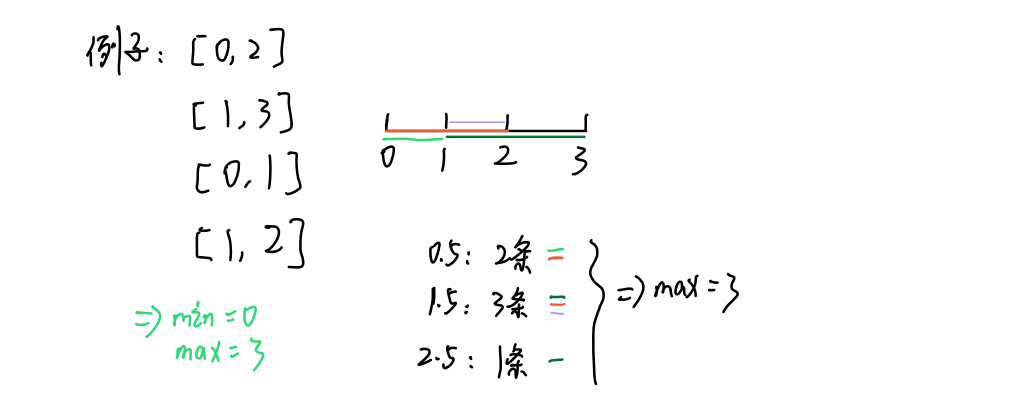
参数说明:

线段重合__牛客网 (nowcoder.com)
求的是某个区域包含多少条线段!
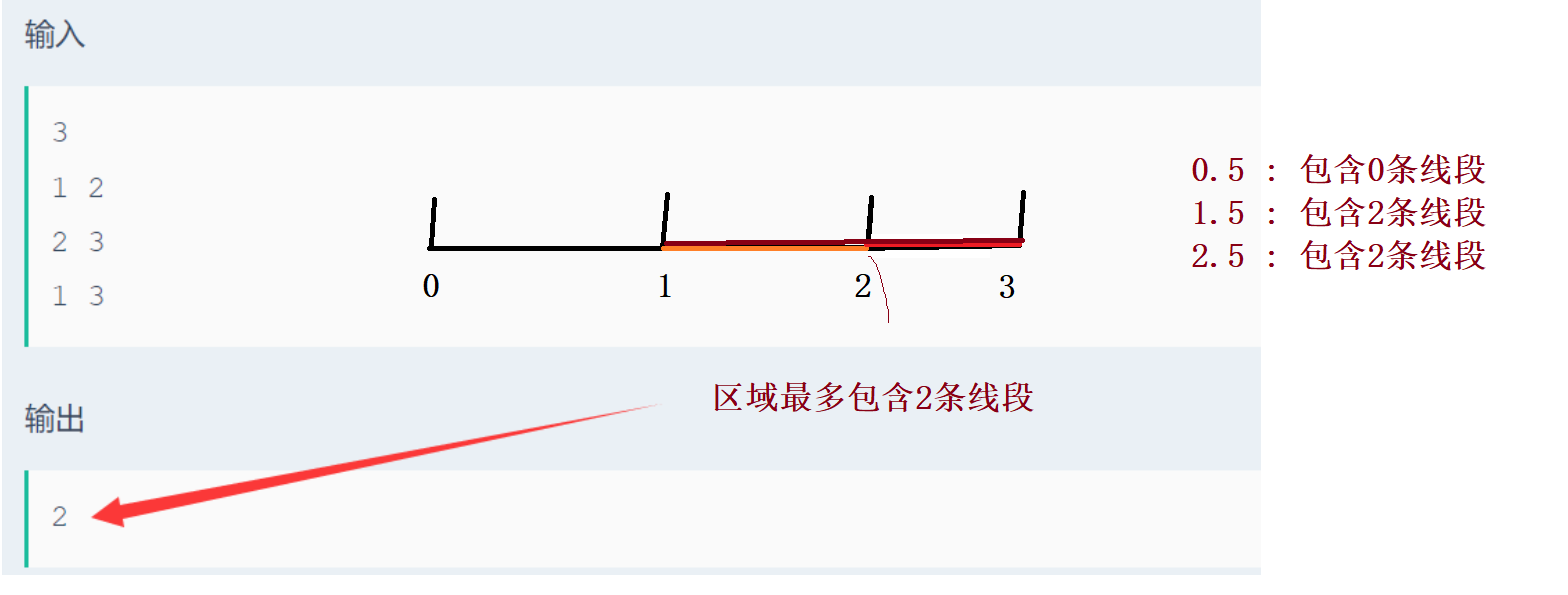
#include<iostream>
#include<vector>
using namespace std;
//线段区间结构体
struct Line
{
int start;//线段起始位置
int end;//线段末尾位置
};
int main()
{
int n;
cin >> n;
vector<Line> v(n); //容器存的是线段区间
//共有n条线段
for (int i = 0; i < n; i++)
{
cin >> v[i].start >> v[i].end;
}
//遍历所有线段,找到起始位置的最小值和末尾位置的最大值
int max = v[0].end;
int min = v[0].start;
for (int i = 0; i < n; i++)
{
if (v[i].end > max)
{
max = v[i].end;
}
if (v[i].start < min)
{
min = v[i].start;
}
}
int maxSum = 0;
//枚举,以每个值+小数开始枚举
for (double p = min + 0.5; p < max + 0.5; p+=1)
{
int sum = 0;
//考察每一个值被多少条线段包含
for (int i = 0; i < n; i++)
{
//被包含:即区间的起始位置<p,区间的末尾位置>p
if (v[i].start<p && v[i].end > p)
{
sum++;
}
}
//更新每条线段被包含的最大值
maxSum = maxSum > sum ? maxSum:sum;
}
cout << maxSum << endl;
}
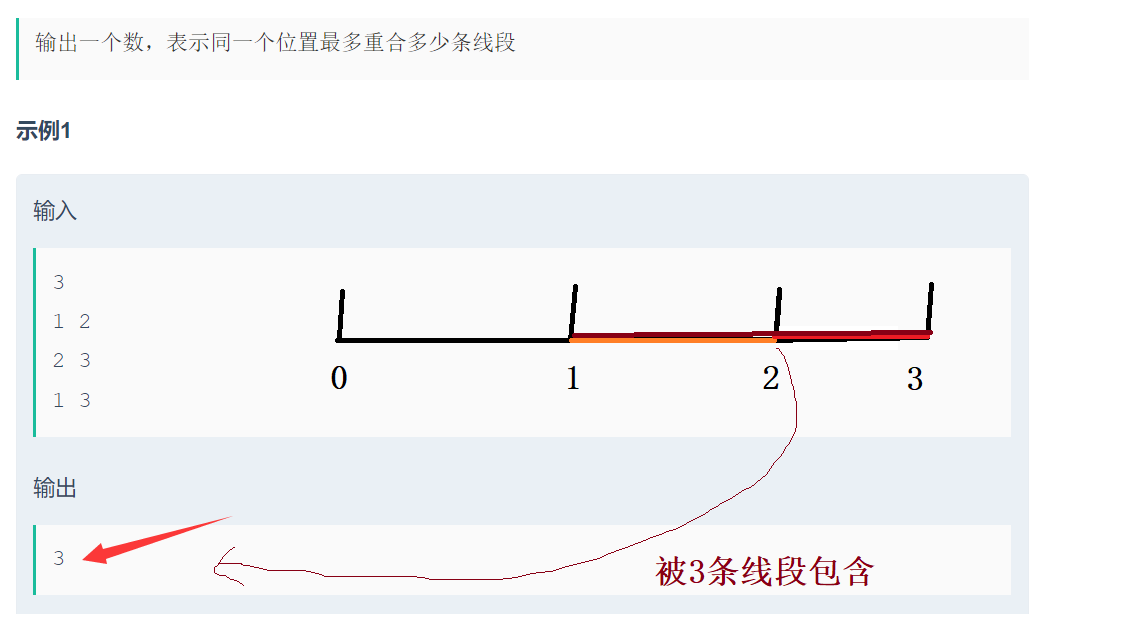
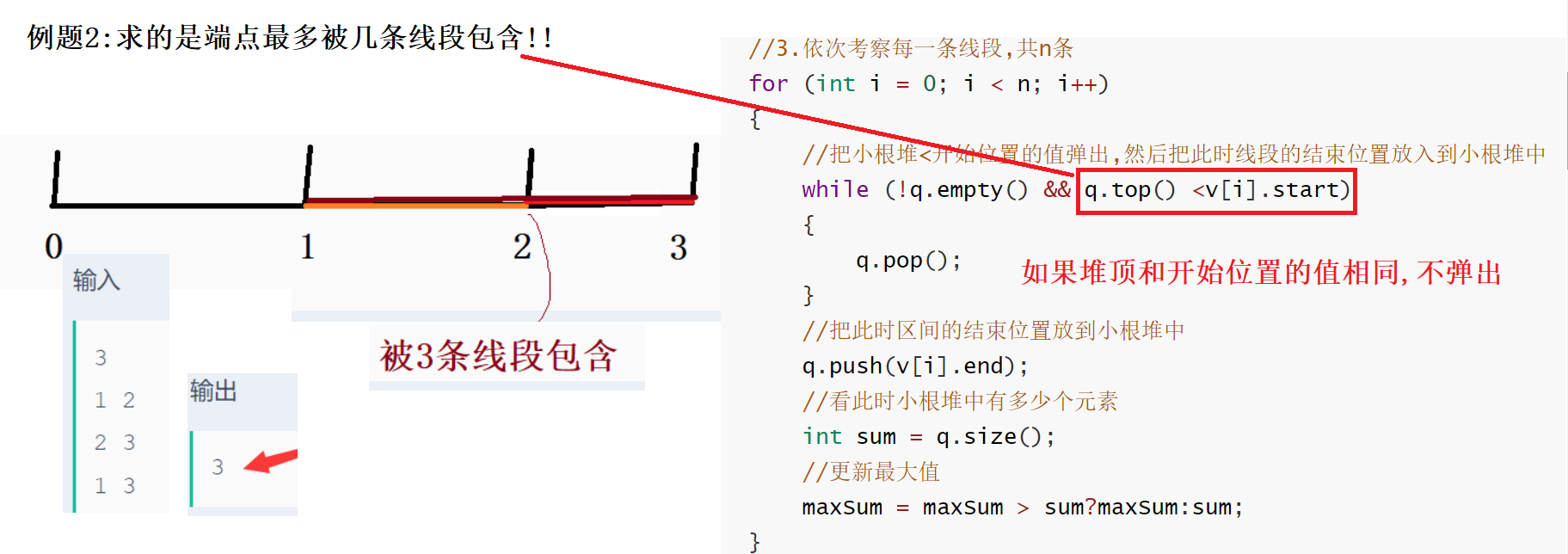
题目2:求的是端点最多被几条线段包含!!
#include<iostream>
#include<vector>
using namespace std;
//线段区间结构体
struct Line
{
int start;//线段起始位置
int end;//线段末尾位置
};
int main()
{
int n;
cin >> n;
vector<Line> v(n); //容器存的是线段区间
//共有n条线段
for (int i = 0; i < n; i++)
{
cin >> v[i].start >> v[i].end;
}
//遍历所有线段,找到起始位置的最小值和末尾位置的最大值
int max = v[0].end;
int min = v[0].start;
for (int i = 0; i < n; i++)
{
if (v[i].end > max)
{
max = v[i].end;
}
if (v[i].start < min)
{
min = v[i].start;
}
}
int maxSum = 0;
//枚举,看每一个端点最多重合多少条线段
for (int p = min ; p < max; p+=1)
{
int sum = 0;
//考察每一个端点被多少条线段包含
for (int i = 0; i < n; i++)
{
//被包含(含有该值在里面):即区间的起始位置<=p,区间的末尾位置>=p
if (v[i].start<=p && v[i].end >= p)
{
sum++;
}
}
//更新每个位置被包含的最大值
maxSum = maxSum > sum ? maxSum:sum;
}
cout << maxSum << endl;
}
方法2:

方法2:使用堆
题目:
线段重合__牛客网 (nowcoder.com)

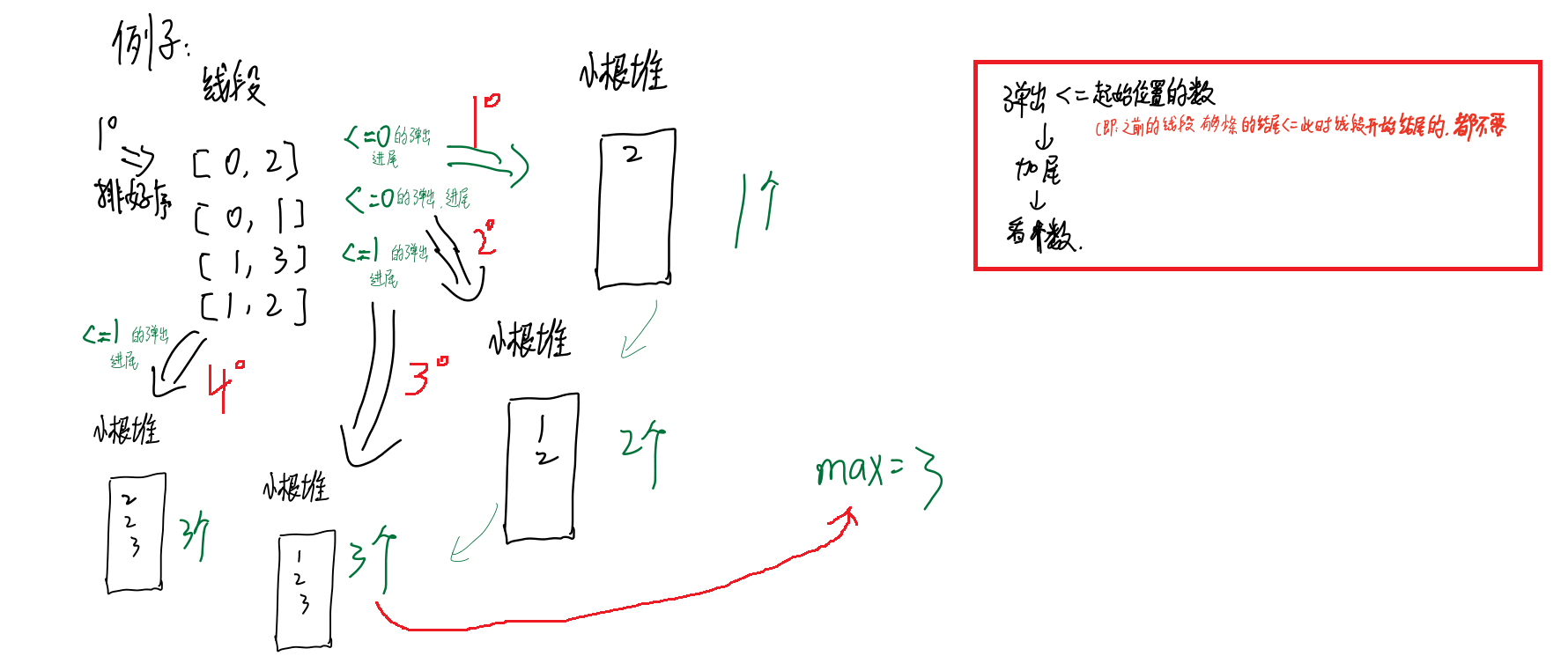
上图解析为例题1的解析
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
//线段区间结构体
struct Line
{
int start;//线段起始位置
int end;//线段末尾位置
};
//注意要传引用
bool cmp(Line& x, Line& y)
{
return x.start < y.start;
}
int main()
{
//将所有线段放入vector中,并根据线段的起始位置排升序
//遍历所有线段,将vector中线段的结束位置放入小根堆q中
//如果小根堆中的有线段的结束位置比当前线段起始位置<=则弹出堆
int n;
cin >> n;
vector<Line> v(n); //容器存的是线段区间
//共有n条线段
for (int i = 0; i < n; i++)
{
cin >> v[i].start >> v[i].end;
}
//1.根据线段的起始位置进行排序
sort(v.begin(), v.end(), cmp);
//2.准备一个小根堆,用于存放区间端点
priority_queue<int, vector<int>, greater<int>> q;
int maxSum = 0;
//3.依次考察每一条线段,共n条
for (int i = 0; i < n; i++)
{
//把小根堆<=开始位置的值弹出,然后把此时线段的结束位置放入到小根堆中
while (!q.empty() && q.top() <=v[i].start)
{
q.pop();
}
//把此时区间的结束位置放到小根堆中
q.push(v[i].end);
//看此时小根堆中有多少个元素
int sum = q.size();
//更新最大值
maxSum = maxSum > sum?maxSum:sum;
}
cout << maxSum << endl;
}
例题2:
线段重合__牛客网 (nowcoder.com)

#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
//线段区间结构体
struct Line
{
int start;//线段起始位置
int end;//线段末尾位置
};
//注意要传引用
bool cmp(Line& x, Line& y)
{
return x.start < y.start;
}
int main()
{
//将所有线段放入vector中,并根据线段的起始位置排升序
//遍历所有线段,将vector中线段的结束位置放入小根堆q中
//如果小根堆中的有线段的结束位置比当前线段起始位置小则弹出堆
int n;
cin >> n;
vector<Line> v(n); //容器存的是线段区间
//共有n条线段
for (int i = 0; i < n; i++)
{
cin >> v[i].start >> v[i].end;
}
//1.根据线段的起始位置进行排序
sort(v.begin(), v.end(), cmp);
//2.准备一个小根堆,用于存放区间端点
priority_queue<int, vector<int>, greater<int>> q;
int maxSum = 0;
//3.依次考察每一条线段,共n条
for (int i = 0; i < n; i++)
{
//把小根堆<开始位置的值弹出,然后把此时线段的结束位置放入到小根堆中
while (!q.empty() && q.top() <v[i].start)
{
q.pop();
}
//把此时区间的结束位置放到小根堆中
q.push(v[i].end);
//看此时小根堆中有多少个元素
int sum = q.size();
//更新最大值
maxSum = maxSum > sum?maxSum:sum;
}
cout << maxSum << endl;
}
上述例题1和例题2有所不同的原因及代码区别:
可以认为例题1中**:端点重合的线段并不算包含**,必须是经过里面的区域 如[1,2] 和[2,3] 端点2重合,但是这两条线段并不包含
而例题2中:端点重合的线段算包含

加强堆的实现
堆的不足之处:
- 1.堆不能做到修改堆中元素的值
- 2.只能删掉堆顶元素,不能删除堆中其他元素,因为这样会破坏堆的结构
如果想要不破坏堆的结构,我们只需要在某个位置重新向上或者向下调整堆即可,但是这样又会有新的问题,那就是修改或删除元素在堆中的位置是未知的,如果想要获取该位置,则需要重新遍历整个堆,时间复杂度为O(N),很显然时间复杂度过高,为了解决这一问题,则需要实现加强堆
上述无法实现的根本原因就是:没有反向索引表
需要实现的接口:
template<class T, class Compare>
class HeapGreater
{
public:
HeapGreater()
{}
//迭代器初始化,用于利用迭代器往堆中插入元素
template<class InputIterator>
HeapGreater(InputIterator first, InputIterator last);
~HeapGreater()
{}
void push(const T& x);
void pop();
//更改obj元素的值为target
void set(const T& obj,const T& target);
//删除堆中指定的值
void erase(const T& obj) ;
T top();//得到堆顶元素
size_t size();//获取堆中元素个数
bool empty();//判断堆是否为空
private:
//需要封装交换函数,因为交换父亲和孩子的值的时候,indexMap中的值也需要交换
void swap(int i, int j);
//向上调整算法,每push一个数都要调用向上调整算法,保证插入后仍是一个堆
void AdjustUp(int child);
//向下调整算法,每次调用pop都要进行向下调整算法重新构成堆
void AdjustDwon(int parent);
//更改某个对象的值,堆结构发生变化,我们需要保持堆结构
void resign(const T& obj);
vector<T> heap;//堆
unordered_map<T, int>indexMap; //反向索引表,记录一个元素在数组中的什么位置,不能使用map,因为key是元素值,如果key相同,不允许冗余
int heapSize ;//堆的元素个数
};
加强堆和普通堆的区别在于多了一个哈希表 unordered_map<T, int>indexMap,其作用是用来记录堆中元素在vector<T> heap的具体下标位置,只要有了具体的下标位置,我们查找的效率就是O(1),对元素进行修改或者删除就非常容易且高效了
所以:在向上或向下调整的时候,不光vector中的元素要交换,indexMap中对应的映射的下标关系也要交换
注意:如果堆中有重复的元素,就会导致unordered_map<T, int>indexMap中的下标无法正确映射,因为哈希表的key不能重复,即使换成能够重复的unordered_multimap也不行,因为要获取其中一个key的下标时,会与其他相同的key产生冲突
那我们如何解决呢?
- 那就是传入对象的指针,而不是传入具体的对象,因为对象的地址是不相同的,另外传指针也会比直接传对象节省很多空间。
HeapGreater.hpp
#pragma once
#include<iostream>
#include<algorithm>
#include<iostream>
#include<vector>
#include<unordered_map>
#include<assert.h>
using namespace std;
//T:数据类型 Com:比较器
template<class T, class Com>
class HeapGreater
{
public:
HeapGreater(int sz = 0)
:heapSize(sz)//初始化堆的元素个数为0
{}
//迭代器初始化,用于利用迭代器往堆中插入元素
template<class InputIterator>
//使用迭代器区间初始化堆
HeapGreater(InputIterator first, InputIterator last)
{
while (first != last)
{
push(*first);//复用push函数
first++;
}
}
~HeapGreater()
{
heap.clear();//清空堆中内容
heapSize = 0;
}
void push(const T& x)
{
heap.push_back(x);
indexMap[x] = heapSize;//在哈希表建立映射关系
AdjustUp(heapSize++);//在heapSize向上调整,然后个数++
}
void pop()
{
assert(!empty()); //防止堆为空,复用empty函数
//堆顶元素和最后一个元素交换,然后删掉最后一个元素,从堆顶位置向下调整
T& tmp = heap[0];
swap(0, --heapSize);
heap.pop_back();
AdjustDwon(0);
//在哈希表中删除tmp的映射
indexMap.erase(tmp);
}
//更改obj的值为target
void set(const T& obj, const T& target)
{
int index = indexMap[obj];//使用哈希表,得到obj在堆中的位置index
heap[index] = target;//将index位置的值改为target
//在哈希表中,删除obj的索引,增加target的索引为index位置
indexMap.erase(obj);
indexMap[target] = index;
//调整堆结构,从index位置进行向上调整/向下调整
//下述代码只执行一个
AdjustDwon(index);
AdjustUp(index);
}
//删除堆中指定的值
//要删除的元素和堆中最后一个位置的元素交换,然后调整
void erase(const T& obj)
{
T& tail = heap[heapSize - 1];
int index = indexMap[obj];//获取obj在堆中的位置index
indexMap.erase(obj);//删除obj在哈希表的映射
heapSize--;
//交换:防止要删的就是最后一个元素!!
if (obj != tail)
{
heap[index] = tail;//堆中index下标的元素变为tail
indexMap[tail] = index;//为tail在哈希表建立映射
resign(tail);//调整,相当于原来index位置的值修改为tail
}
heap.pop_back();//弹出要被删除的obj元素
}
//得到堆顶元素
T top()
{
//防止堆为空
assert(!empty());//复用empty函数
return heap[0];
}
//获取堆中元素个数
size_t size()
{
return heapSize;
}
//判断堆是否为空
bool empty()
{
return heapSize == 0;
}
private:
//需要封装交换函数,因为交换父亲和孩子的值的时候,indexMap中的值也需要交换
//i和j是要交换的两个元素的下标
void swap(int i, int j)
{
//根据下标得到其对应值
T h1 = heap[i];
T h2 = heap[j];
//交换两个元素的值
heap[i] = h2;
heap[j] = h1;
//更改在哈希表的映射位置
indexMap[h1] = j;
indexMap[h2] = i;
}
//向上调整算法,每push一个数都要调用向上调整算法,保证插入后仍是一个堆
void AdjustUp(int child)
{
//Com是比较器,模板参数
Com cmp;
int parent = (child - 1) / 2;
//最坏调整到根节点
while (child)
{
if (cmp(heap[parent], heap[child]))
{
swap(parent, child);//复用swap函数,传下标,内部会处理
//迭代往上走
child = parent;
parent = (child - 1) / 2;
}
else
{
break;//已经满足堆结构了
}
}
}
//向下调整算法,每次调用pop都要进行向下调整算法重新构成堆
void AdjustDwon(int parent)
{
Com cmp;
int child = parent * 2 + 1;//默认为左孩子
//最坏调整到叶子
while (child < heapSize)
{
//用比较器选出要的的孩子,要防止没有右孩子
if (child + 1 < heapSize && cmp(heap[child], heap[child + 1]))
{
child++;//要的是右孩子
}
if (cmp(heap[parent], heap[child]))
{
swap(parent, child);//复用swap函数,传下标,内部会处理
//迭代往下走
parent = child;
child = parent * 2 + 1;
}
else
{
break;//满足堆结构了
}
}
}
//更改某个对象的值,堆结构发生变化,我们需要保持堆结构
void resign(const T& obj)
{
//obj对象的值发生改变,要从obj所在堆中的下标位置进行调整
int index = indexMap[obj];//获取obj对象在堆中的下标
//执行向上调整 / 向下调整 / 不调整 下面两个代码只执行1个 / 不执行
AdjustDwon(index);
AdjustUp(index);
}
vector<T> heap;//堆
unordered_map<T,int> indexMap; //反向索引表,记录一个元素在数组中的什么位置,不能使用map,因为key是元素值,如果key相同,不允许冗余
int heapSize;//堆的元素个数
};
//for test
void test_HeapGreater1()
{
HeapGreater<string, less<string>> heap;
heap.push("a");
heap.push("c");
heap.push("b");
heap.push("d");
heap.push("e");
heap.push("z");
heap.push("x");
heap.erase("e");
heap.set("c", "new c");
while (!heap.empty())
{
cout << heap.top() << endl;
heap.pop();
}
}
struct cmp
{
//比较的对象是string*类型对象
bool operator()(string*& l, string*& r)
{
return *l < *r;//比较string对象,根据ascii比较
}
};
void test_HeapGreater2()
{
string* s1 = new string("a");
string* s2 = new string("c");
string* s3 = new string("b");
string* s4 = new string("d");
string* s5 = new string("e");
string* s6 = new string("e");
string* s7 = new string("z");
string* s8 = new string("new c");
HeapGreater<string*, cmp> heap;
heap.push(s1);
heap.push(s2);
heap.push(s3);
heap.push(s4);
heap.push(s5);
heap.push(s6);
heap.push(s7);
heap.erase(s5);
heap.set(s2, s8);
while (!heap.empty())
{
cout << *heap.top() << endl;
heap.pop();
}
}
void test_HeapGreater3()
{
vector<string>v = { "a" ,"c" ,"b" ,"d" ,"e" ,"x" ,"z" };
HeapGreater<string, less<string>> heap(v.begin(), v.end());
heap.erase("e");
heap.set("c", "new c");
while (!heap.empty())
{
cout << heap.top() << endl;
heap.pop();
}
}