欢迎来到我的:世界
希望作者的文章对你有所帮助,有不足的地方还请指正,大家一起学习交流 !
目录
- 前言
- 队列的实现
- 层序遍历详解
- 强化练习
- 1.判断是不是完全二叉树
- 求二叉树的最大深度
- 总结
前言
国庆到了,也要内卷一下,感谢所以老铁们的支持!😎
队列的实现
1、队列的定义
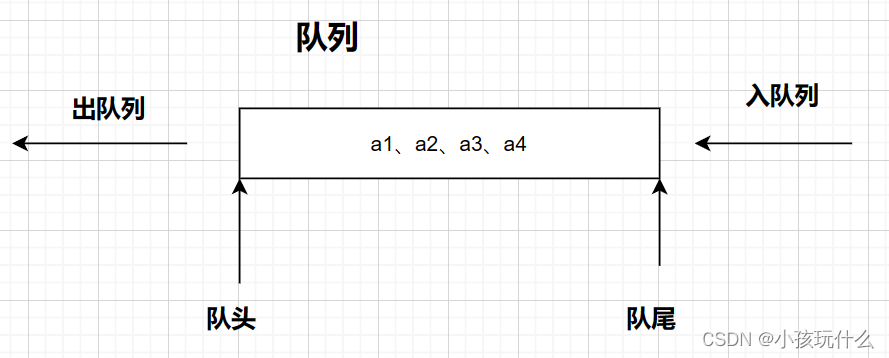
队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列是一种先进先出(First In First Out)的线性表,简称FIFO。允许插入的一端称为队尾,允许删除的一端称为队头;
队头(Front):允许删除的一端,又称队首。
队尾(Rear):允许插入的一端。
空队列:不包含任何元素的空表。
链式队列存储类型:
typedef int QDatatype;
typedef struct QueueNode
{
QDatatype val;//记录每个节点的值
struct QueueNode* next;//下一个节点
}QueueNode;
typedef struct Queue
{
QueueNode* head;//队列的头指针
QueueNode* tail;//队列的尾指针
int size;//记录队列的元素个数,开始为0;
}Queue;
队列的常见基本操作:
//初始化队列,构造一个空队列pd。
void QueueInit(Queue* pd);
//清除队列,将队列清除,以免空间泄露
void Queuedestroy(Queue* pd);
//入队,若队列pd未满,将x加入,使之成为新的队尾。
void Queuepush(Queue* pd, QDatatype x);
//出队,若队列pd非空,删除队头元素。
void QueuePop(Queue* pd);
//读取队头元素值,并返回值
QDatatype QueueFront(Queue* pd);
//判队列空,若队列pd为空返回true,否则返回false。
bool QueueEmpty(Queue* pd);
链队列初始化
void QueueInit(Queue* pd)
{
//构造一个空队列
pd->head = pd->tail = NULL;
pd->size = 0;
}
链队列入队
void Queuepush(Queue* pd, QDatatype x)
{
assert(pd);
QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
if (newnode == NULL)
{
perror("malloc");
exit(-1);
}
newnode->next = NULL;
newnode->val = x;
if (pd->tail == NULL)
{
pd->head = pd->tail = newnode;
}
else
{
pd->tail->next = newnode;
pd->tail = newnode;
}
pd->size++;
}
出队列,删除队头元素
void QueuePop(Queue* pd)
{
assert(pd);
assert(!QueueEmpty(pd));
if (pd->head->next == NULL)
{
free(pd->head);
pd->tail = pd->head = NULL;
}
else
{
QueueNode* next = pd->head->next;
free(pd->head);
pd->head = next;
}
pd->size--;
}
读取队头元素
QDatatype QueueFront(Queue* pd)
{
assert(pd);
assert(!QueueEmpty(pd));
return pd->head->val;
}
判队列空,若队列pd为空返回true,否则返回false。
bool QueueEmpty(Queue* pd)
{
assert(pd);
return pd->head == NULL;
}
清除队列,释放空间
void Queuedestroy(Queue* pd)
{
assert(pd);
QueueNode* cur = pd->head;
while (cur)
{
QueueNode* next = cur->next;
free(cur);
cur = next;
}
pd->head = pd->tail = NULL;
pd->size = 0;
}
层序遍历详解
紧接上回,以层来访问,一层一层往下访问,每一层是从左往右访问;
这里用到了队列,将根节点先A存入队列中,然后再将其子节点a b存入队列,再取出根节点A,上述操作为一个循环;而后在存入上一次存入a b 他们分别的子节点,然后在取出来,依次执行操作下去,就是层序遍历;
图解:
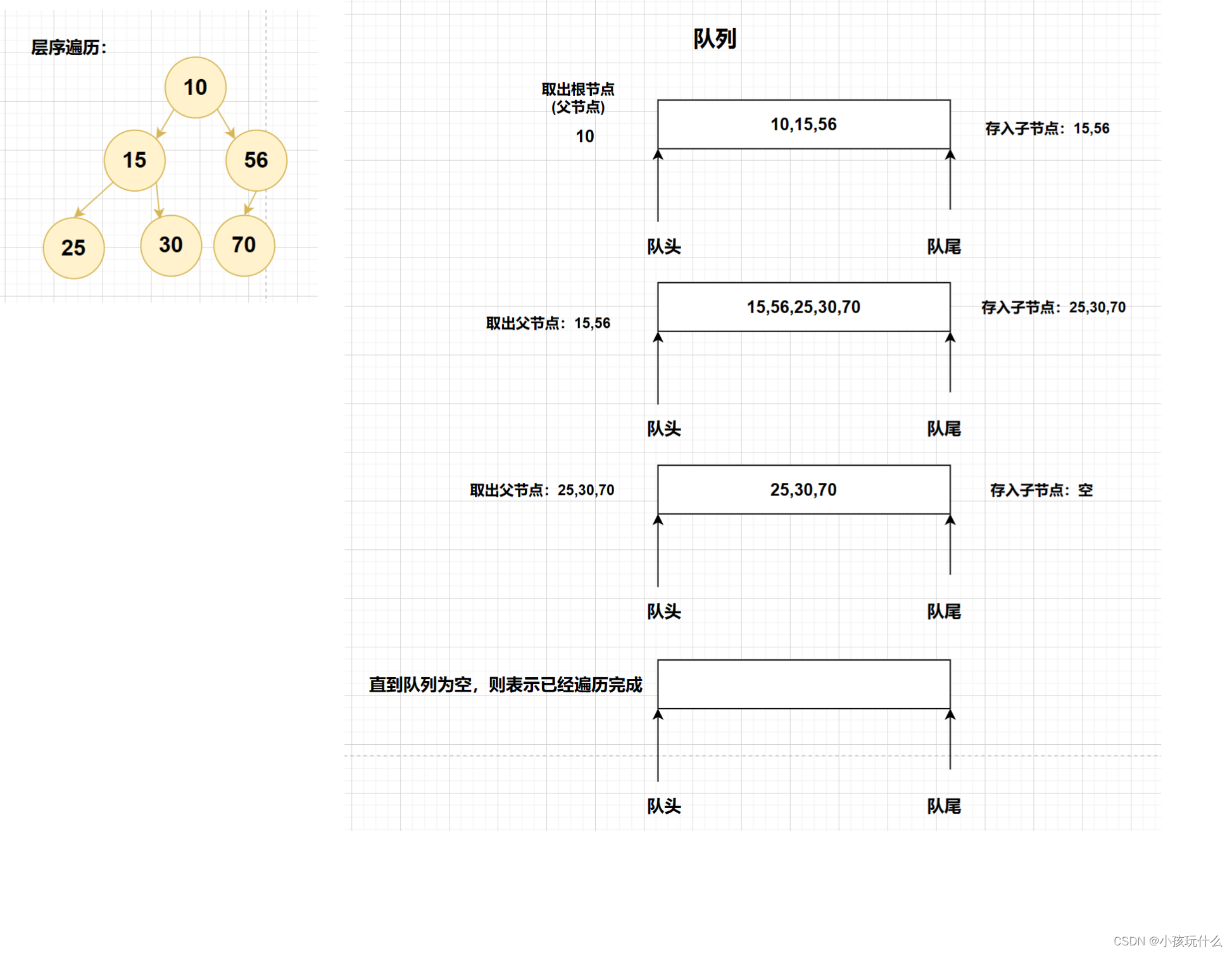
代码实现:
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);//队列初始化
//如果根节点不为空,则将其存入队列
if (root)
{
Queuepush(&q, root);
}
//直到队列为空则代表遍历完成
while (!QueueEmpty(&q))
{
BTNode* tem = QueueFront(&q);
printf("%d ", tem->val);
if (tem->left)//是避免NULL也存入到队列中去
Queuepush(&q, tem->left);
if (tem->right)//是避免NULL也存入到队列中去
Queuepush(&q, tem->right);
QueuePop(&q);
}
Queuedestroy(&q);
}
强化练习
1.判断是不是完全二叉树
地址:oj地址
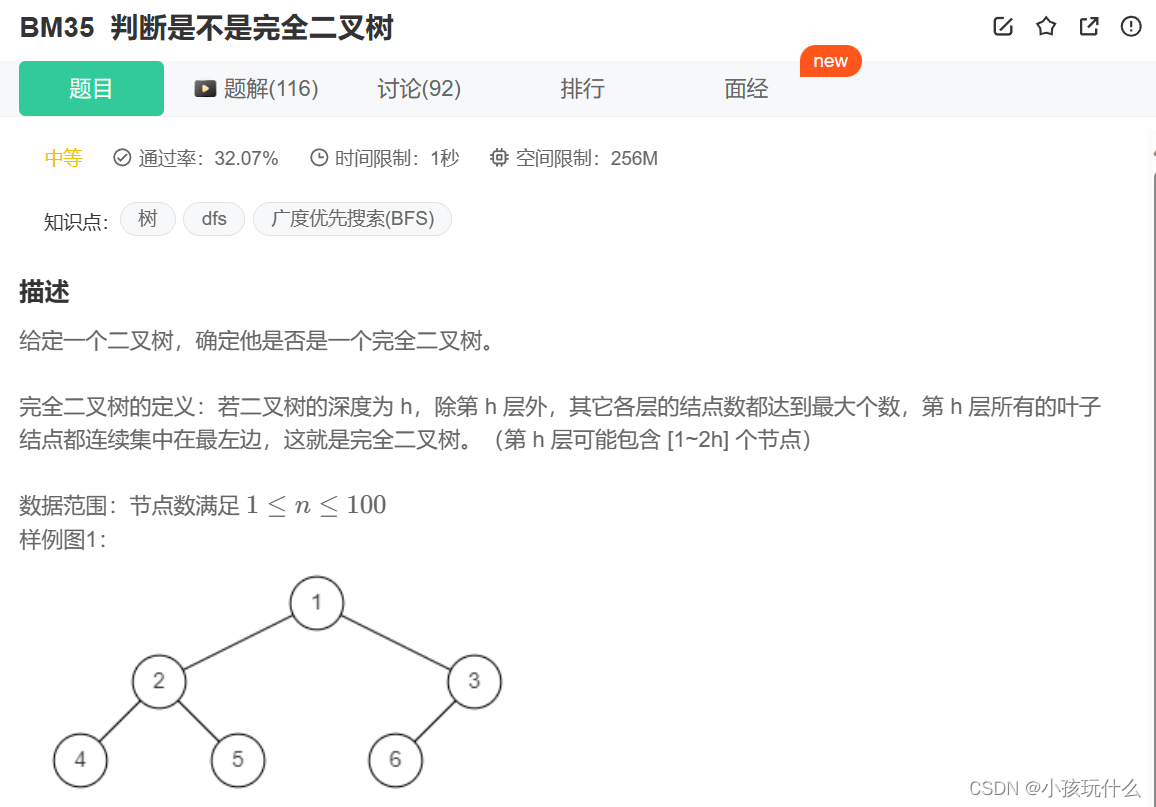
解题思路:
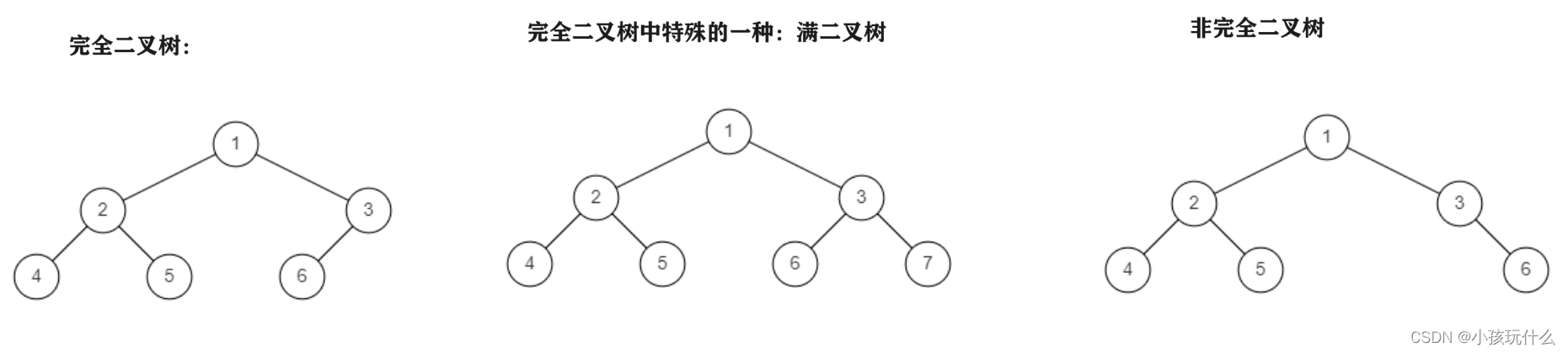
要知道完全二叉树是一种什么样的结构:
所以这道题可以通过层序遍历的方式来解决;
可以看出:完全二叉树的非空节点是连续的,而非完全二叉树的非空节点不是连续的;可以根据这点来解决问题;
int BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
Queuepush(&q, root);
}
//层序遍历出最后一个叶节点,找到第一个空节点
while (!QueueEmpty(&q))
{
BTNode* tem = QueueFront(&q);
if (tem == NULL)
break;
//这是将空节点也存入到了队列中
Queuepush(&q, tem->left);
Queuepush(&q, tem->right);
QueuePop(&q);
}
//找到了空节点,继续往下找
while (!QueueEmpty(&q))
{
BTNode* tem = QueueFront(&q);
QueuePop(&q);
if (tem)//如果有一个几点不为空节点,则代表不是连续的空节点,则代表该不是完全二叉树,返回false;
{
Queuedestroy(&q);
return false;
}
}
//否则给该空节点是连续的,证明是完全二叉树,返回true
Queuedestroy(&q);
return true;
}
求二叉树的最大深度
地址oj地址
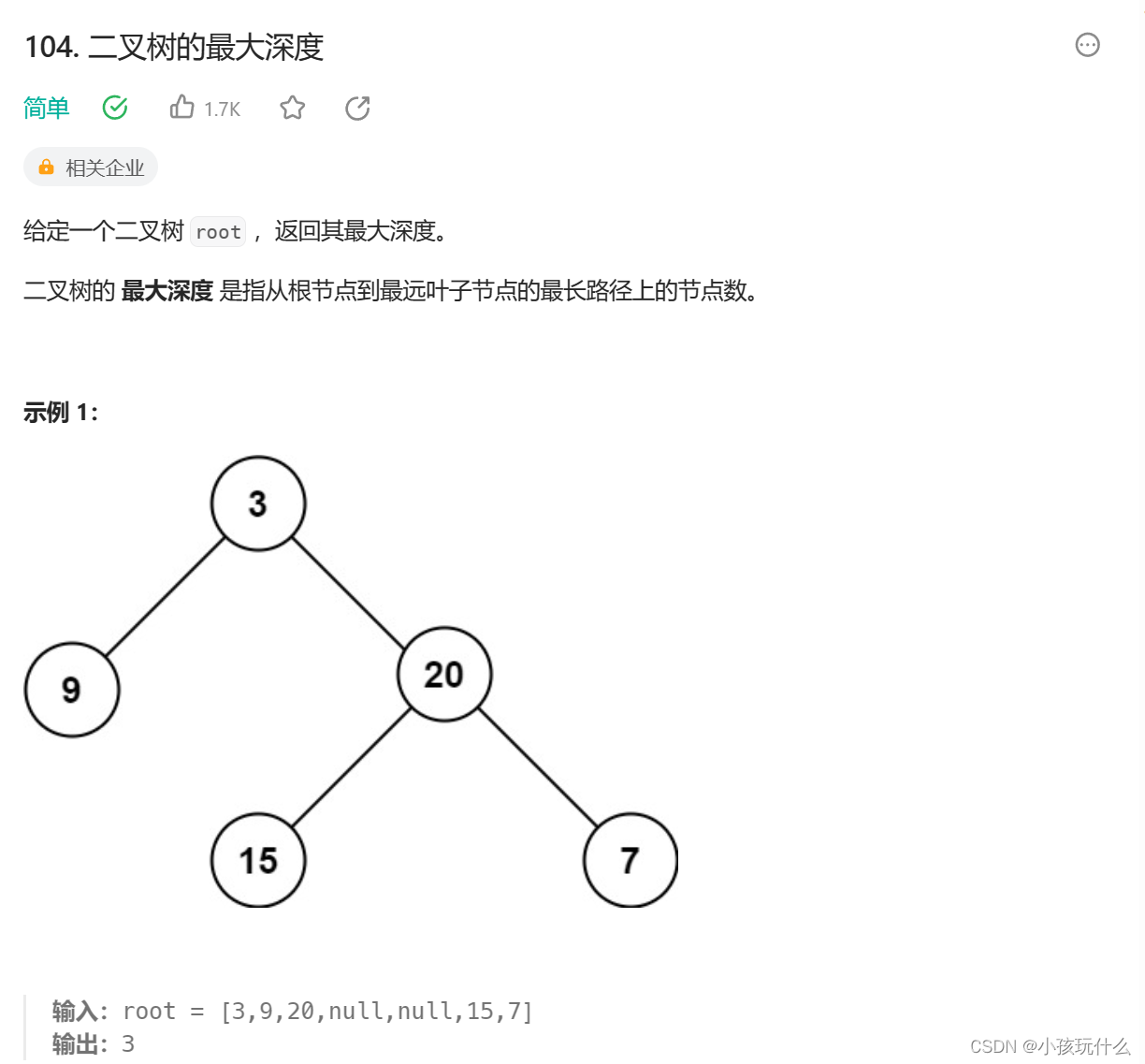
解题思路:
树的最大深度也就是其最大的高度;求高度的一个思路:
根节点高度=其左右子节点高度高的+1;
具体代码实现:
int maxDepth(struct TreeNode* root){
if(root==NULL)
return 0;
int left=maxDepth(root->left);
int right=maxDepth(root->right);
return left>right?left+1:right+1;
}
如果你知道一个函数fmax那就更简单了;该函数就是用来求两个值返回大的那一个;
代码实现:
int maxDepth(struct TreeNode* root){
if(root==NULL)
return 0;
return fmax(maxDepth(root->left),maxDepth(root->right))+1;
}
总结
到了最后:感谢支持
我还想告诉你的是:
------------对过程全力以赴,对结果淡然处之
也是对我自己讲的