课程地址和说明
损失函数p2
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
损失函数
损失函数是用来衡量预测值 y ^ \hat{y} y^或 y ′ y' y′与真实值 y y y的差别,下面给出常见的损失函数类型:
均方损失函数(L2 LOSS)
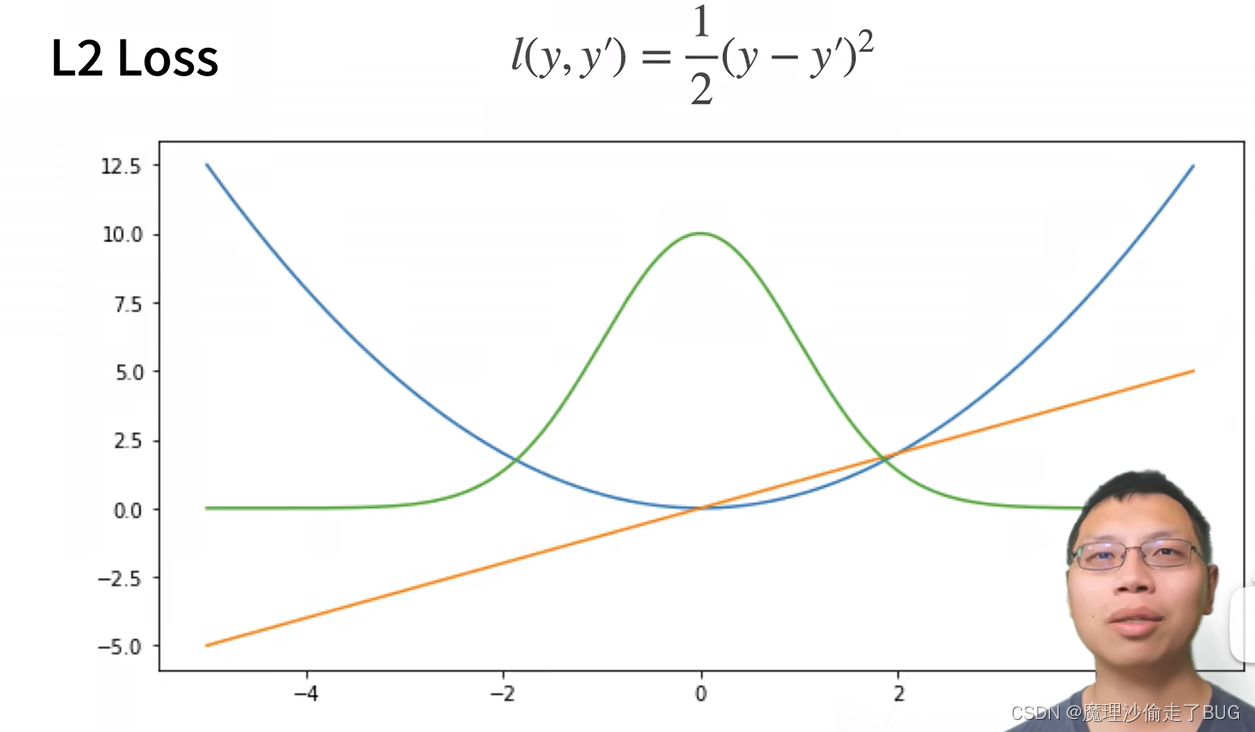
【注】蓝色的线是它的二次函数图像,绿色的线是它的似然函数
e
−
l
e^{-l}
e−l, 它的似然函数为高斯分布,橙色的线表示的是损失函数的梯度。当预测值
y
′
y'
y′和真实值
y
y
y距离比较远的时候,则损失函数的梯度比较大,参数更新比较多,当预测值越来越靠近真实值,损失函数的梯度会变得越来越小。
【提问】请用通俗的语言解释一下何为似然函数,其用途是什么,什么是高斯分布?
【chatGPT回答】好的,我会尽量用简单的话来解释这些概念。
- 似然函数:
想象你有一个盒子,里面混合了红球和蓝球。你闭上眼睛摸出了10个球,结果有7个红球和3个蓝球。现在你想知道这个盒子中红球和蓝球的比例,但是你不能直接去数每种球有多少个。
似然函数就是一个帮你估计这个比例的方法。你根据摸出的球的比例,反过来估计整个盒子里红球和蓝球的比例。似然函数描述了在不同的比例假设下,观察到现有数据(你摸出的10个球的颜色)的可能性。
用途:似然函数在统计学和机器学习中经常用于参数估计。例如,我们想要估计一个模型的参数,可以通过找到使似然函数最大的参数值来实现。- 高斯分布:
高斯分布,也叫正态分布或“钟形曲线”,是一种描述数据分布的方式,特点是中间最高,两边逐渐减小,形状像一个钟。例如,人类的身高分布:大部分人的身高都集中在平均值附近,少数人的身高非常矮或非常高。
为什么我们经常听到高斯分布?因为在现实生活中,许多随机现象的分布都接近或遵循高斯分布。例如,实验测量误差、人们的考试成绩等。
高斯分布可以由两个参数描述:均值(平均值)和标准差(描述数据的离散程度)。
希望这些解释对您有帮助!
【提问】请加一些具体示例和数学计算
【chatGPT回答】好的,我们再进一步详细探讨这两个概念。- 似然函数:
设想一个简单的场景:你有一枚不公正的硬币,抛出正面的概率是 p p p,抛出反面的概率是 1 − p 1-p 1−p。现在你抛了这枚硬币3次,结果观测到了2次正面和1次反面。那么,似然函数就是描述在给定不同的 p p p值(也就是正面出现的概率)下,观察到这组数据(2次正面,1次反面)的概率。
数学上,这个似然函数可以写成:
L ( p ) = p 2 ( 1 − p ) L(p) = p^2(1-p) L(p)=p2(1−p)
如果你想知道哪个 p p p值最有可能,就需要找到使得 L ( p ) L(p) L(p)最大的 p p p值。- 高斯分布:
高斯分布的数学形式是:
f ( x ) = 1 σ 2 π e − 1 2 ( x − μ σ ) 2 f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} f(x)=σ2π1e−21(σx−μ)2
其中, μ \mu μ是均值, σ \sigma σ是标准差。
示例:假设某高中学生的数学考试成绩遵循高斯分布,均值是70分,标准差是10分。那么,一个学生分数是80分的概率密度是:
f ( 80 ) = 1 10 2 π e − 1 2 ( 80 − 70 10 ) 2 f(80) = \frac{1}{10 \sqrt{2\pi}} e^{-\frac{1}{2}(\frac{80-70}{10})^2} f(80)=102π1e−21(1080−70)2
计算这个值,你就能知道80分这个成绩在整个分布中的相对位置。
需要注意的是,上述给出的是概率密度,不是概率。如果想知道一个学生考分数在70到80分之间的概率,需要对上述函数在这个区间内积分。
希望这些具体的示例和数学计算可以帮助你更好地理解这两个概念!
当预测值和真实值离得较远的时候,不一定要用大梯度来更新参数,所以用下面的损失函数:
绝对值损失函数(L1 LOSS)

【注】蓝色的线是损失函数曲线,绿色是似然函数,橙色是梯度。
鲁棒损失函数
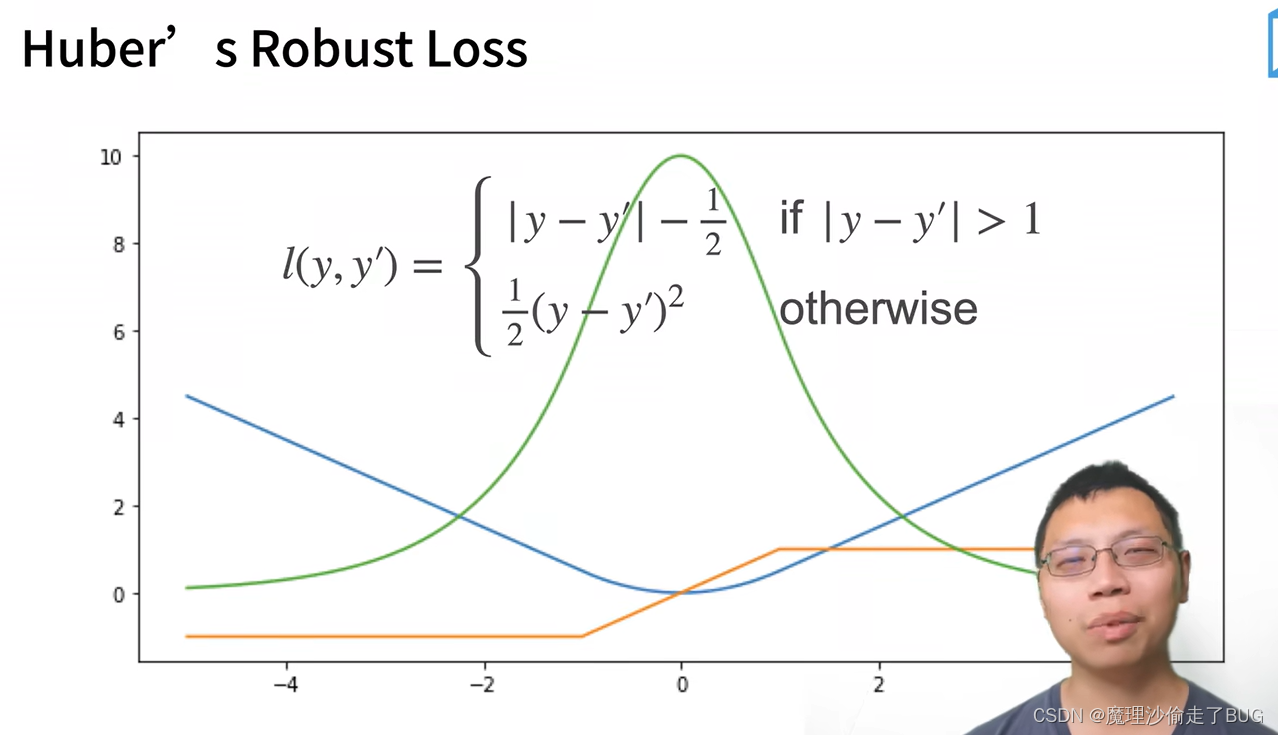
【提问】用通俗的语言列出并解释深度学习常见的损失函数及其用法
【chatGPT回答】深度学习中的损失函数是衡量模型预测结果与真实值之间差异的一种方法。选择适当的损失函数对于模型的性能至关重要。下面是一些常见的损失函数及其通俗解释和应用场景:
- 均方误差损失(Mean Squared Error, MSE):
通俗解释:计算模型预测值与真实值之间的平方差的平均值。差异越大,损失值越高。
用途:常用于回归问题,如预测房价、股票价格等。
MSE = 1 n ∑ i = 1 n ( y i − y i ^ ) 2 \text{MSE} = \frac{1}{n} \sum\limits_{i=1}^n (y_i - \hat{y_i})^2 MSE=n1i=1∑n(yi−yi^)2- 交叉熵损失(Cross Entropy Loss):
通俗解释:衡量模型预测的概率分布与真实的概率分布之间的差异。差异越大,损失值越高。
用途:常用于分类问题,如图像识别、文本分类等。
CrossEntropy = − ∑ i = 1 n y i log ( y i ^ ) \text{CrossEntropy} = -\sum\limits_{i=1}^n y_i \log(\hat{y_i}) CrossEntropy=−i=1∑nyilog(yi^)- 二元交叉熵损失(Binary Cross Entropy Loss):
通俗解释:是交叉熵损失的特殊情况,适用于二分类问题。
用途:如垃圾邮件识别、病症检测等。
BinaryCrossEntropy = − ∑ i = 1 n ( y i log ( y i ^ ) + ( 1 − y i ) log ( 1 − y i ^ ) ) \text{BinaryCrossEntropy} = -\sum\limits_{i=1}^n (y_i \log(\hat{y_i}) + (1 - y_i) \log(1 - \hat{y_i})) BinaryCrossEntropy=−i=1∑n(yilog(yi^)+(1−yi)log(1−yi^))- 绝对平均误差损失(Mean Absolute Error, MAE):
通俗解释:计算模型预测值与真实值之间的绝对差的平均值。差异越大,损失值越高。
用途:也常用于回归问题,与MSE损失类似。
MAE = 1 n ∑ i = 1 n ∣ y i − y i ^ ∣ \text{MAE} = \frac{1}{n} \sum\limits_{i=1}^n |y_i - \hat{y_i}| MAE=n1i=1∑n∣yi−yi^∣- Hinge 损失:
通俗解释:常用于“最大间隔”分类,尤其是支持向量机(SVM)。
用途:用于二分类问题,也可以扩展到多分类问题。
Hinge Loss = ∑ i = 1 n max ( 0 , 1 − y i ⋅ y i ^ ) \text{Hinge Loss} = \sum\limits_{i=1}^n \max(0, 1 - y_i \cdot \hat{y_i}) Hinge Loss=i=1∑nmax(0,1−yi⋅yi^)- Huber 损失:
通俗解释:是均方误差与绝对误差的结合,对于较小的误差使用平方误差,对于较大的误差使用线性误差。
用途:用于回归问题,尤其是在存在噪声数据时。
Huber Loss = { 1 2 ( y i − y i ^ ) 2 , 对于 ∣ y i − y i ^ ∣ ≤ δ δ ( ∣ y i − y i ^ ∣ − 1 2 δ ) , 其他 \text{Huber Loss} = \begin{cases} \frac{1}{2}(y_i - \hat{y_i})^2,\text{对于 } |y_i - \hat{y_i}| \le \delta \ \\\delta(|y_i - \hat{y_i}| - \frac{1}{2}\delta) , \text{其他} \end{cases} Huber Loss={21(yi−yi^)2,对于 ∣yi−yi^∣≤δ δ(∣yi−yi^∣−21δ),其他
这些损失函数在训练深度学习模型时扮演着至关重要的角色,帮助优化算法找到使损失最小的模型参数。选择适当的损失函数可以大大提高模型的性能和准确性。