本文这里是对CSDN上另一位博主的代码进行了整理：

基于opencv的裂缝宽度检测算法（计算轮廓最大内切圆算法）

我觉得这位博主应该是上传了一个代码草稿，我对其进行了重新整理，并添加了详细的注释。

import cv2
import math
import random
import numpy as np
from numpy.ma import cos, sin
import pyzjr as pz

class Maximum_width:
    def findContous(self,img):
        kernel = np.ones((1, 5), np.uint8)
        thresh=pz.BinaryImg(img)
        thresh = cv2.morphologyEx(thresh, cv2.MORPH_CLOSE, kernel, anchor=(2, 0), iterations=5)
        contous, hierarchy = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
        return contous

    def Extract_repeat_points(self,contour,Bbox):
        """
        从给定多边形轮廓内提取位于矩形区域内的点。
        :param contour: 多边形轮廓点集
        :param Bbox: 矩形区域的边界坐标信息[left_x, up_y, right_x, down_y]
        :return: 位于多边形内且在矩形区域内的点数组
        """
        left_x, up_y, right_x, down_y=Bbox
        Nx = 2 ** 8
        Ny = 2 ** 8
        pixel_X = np.linspace(left_x, right_x, Nx)
        pixel_Y = np.linspace(up_y, down_y, Ny)
        xx, yy = np.meshgrid(pixel_X, pixel_Y)

        mask = np.zeros(xx.shape, dtype=bool)
        for i in range(xx.shape[0]):
            for j in range(xx.shape[1]):
                if cv2.pointPolygonTest(contour, (xx[i, j], yy[i, j]), False) > 0:
                    mask[i, j] = True

        in_point = np.column_stack((xx[mask], yy[mask]))
        return in_point

    def find_max_radius(self,contous, pixelx, pixely, small_r, big_r, precision):
        """
        在给定轮廓内查找最大半径。
        :param contours: 轮廓
        :param pixelx: 圆心的像素 x 坐标
        :param pixely: 圆心的像素 y 坐标
        :param small_r: 最小半径
        :param big_r: 最大半径
        :param precision: 精度
        :return: 最大半径
        """
        radius = small_r
        L = np.linspace(0, 2 * math.pi, 360)
        circle_X = pixelx + radius * cos(L)
        circle_Y = pixely + radius * sin(L)
        for i in range(len(circle_Y)):
            if cv2.pointPolygonTest(contous, (circle_X[i], circle_Y[i]), False) < 0:
                return 0
        while big_r - small_r >= precision:
            half_r = (small_r + big_r) / 2
            circle_X = pixelx + half_r * cos(L)
            circle_Y = pixely + half_r * sin(L)
            if_out = False
            for i in range(len(circle_Y)):
                if cv2.pointPolygonTest(contous, (circle_X[i], circle_Y[i]), False) < 0:  # 如果圆散集有在轮廓之外的点
                    big_r = half_r
                    if_out = True
            if not if_out:
                small_r = half_r
        radius = small_r
        return radius

    def find_optimal_information(self,in_point,big_r,precision,contous,sample_ratio=0.01):
        """
        从一组点中寻找具有最大内切圆半径的点。
        :param in_point: 点集合
        :param big_r: 内切圆最大半径
        :param precision: 精度
        :param contous: 多边形轮廓
        :param sample_ratio: 采样比例
        :return: 具有最大内切圆半径的点的坐标和半径
        """
        num_points = len(in_point)
        num_samples = max(1, int(num_points * sample_ratio))
        sampled_indices = random.sample(range(num_points), num_samples)
        sampled_indices.sort()
        best_radius = 0
        center = None
        for idx in sampled_indices:
            point = in_point[idx]
            max_radius_for_point = self.find_max_radius(contous, point[0], point[1], best_radius, big_r, precision)
            if max_radius_for_point > best_radius:
                best_radius = max_radius_for_point
                center = point

        remaining_indices = [i for i in range(num_points) if i not in sampled_indices]
        for idx in remaining_indices:
            point = in_point[idx]
            max_radius_for_point = self.find_max_radius(contous, point[0], point[1], best_radius, big_r, precision)
            if max_radius_for_point > best_radius:
                best_radius = max_radius_for_point
                center = point

        return best_radius, center

    def FindmaxIncircle(self, circle_list):
        """
        在裂缝最大内切圆信息中找到具有最大半径的内切圆的中心坐标和半径。
        :param circle_list: 裂缝最大内切圆信息列表，每个元素为 [radius, center]
        :return: 最大半径的内切圆的中心坐标和半径
        """
        max_radius = max(circle_list, key=lambda x: x[0])[0]
        max_center = next(item for item in circle_list if item[0] == max_radius)[1]
        return max_center, max_radius


    def draw_contous_circle(self,original_img, contours, circle_list, max_radius, max_center):
        """
        在原始图像上绘制轮廓及内切圆。
        :param original_img: 原始图像
        :param contours: 轮廓列表
        :param circle_list: 扩展圆信息列表
        :param max_radius: 最大内切圆半径
        :param max_center: 最大内切圆中心
        :return: 绘制了轮廓和内切圆的图像
        """
        cv2.drawContours(original_img, contours, -1, (0, 0, 255), -1)
        for circle_info in circle_list:
            radius, center = circle_info[:2]
            color = (255, 0, 0) if radius == max_radius else (255, 245, 0)
            if radius == max_radius:
                cv2.circle(original_img, (int(max_center[0]), int(max_center[1])), int(max_radius), color, 2)
            else:
                cv2.circle(original_img, (int(center[0]), int(center[1])), int(radius), color, 2)

        return original_img

def dealwith_inCircle(img,imgoriginal,showCircle=True):
    """
    处理内切圆问题并显示结果。
    :param img: 输入处理的标签图像
    :param img_original: 对应的原始图像
    :param show_circle: 是否显示内切圆结果，默认为 True
    """
    mac = Maximum_width()
    contous = mac.findContous(img)
    expansion_circle_list = []
    for con in contous:
        left_x, right_x, down_y, up_y = np.min(con[:, 0, 0]), np.max(con[:, 0, 0]), np.max(con[:, 0, 1]), np.min(con[:, 0, 1])
        Bbox=[left_x, up_y, right_x, down_y]
        upper_r = min(right_x - left_x, down_y - up_y) / 2
        precision = math.sqrt((right_x - left_x) ** 2 + (down_y - up_y) ** 2) / (2 ** 13)      #获得二分精度
        in_point=mac.Extract_repeat_points(con, Bbox)
        radius,center=mac.find_optimal_information(in_point,upper_r,precision,con)
        expansion_circle_list.append([radius, center])
    max_center,max_radius=mac.FindmaxIncircle(expansion_circle_list)
    if showCircle:
        Circle=mac.draw_contous_circle(imgoriginal,contous,expansion_circle_list,max_radius,max_center)
        cv2.imshow("Maximum Inscribed Circle",Circle)
        cv2.waitKey(0)
    return round(max_radius*2,2)

if __name__=="__main__":
    from pyzjr.dlearn.tools import Runcodes
    with Runcodes("最大内切圆算法"):
        path = r"D:\PythonProject\RoadCrack\dimension2_data\num/024.png"  # 分割图
        path2 = r"D:\PythonProject\RoadCrack\dimension2_data\image/013.jpg"  # 对应的原图
        img = cv2.imread(path)
        img2 = cv2.imread(path2)
        width=dealwith_inCircle(img,img2,False)
        print(f'最大宽度:{round(width, 2)}')

最大宽度:13.84

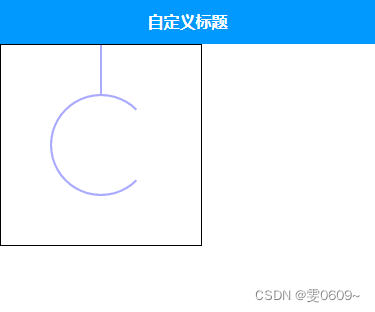
将标签图放大，可以数一数确实还可以，大致在13左右。使用的方式是通过从给定的轮廓中提取点，并使用二分法来查找最大内切圆的半径。它通过在多个采样点上尝试不同的半径大小，验证这些半径是否有效来确定最大内切圆。最后，绘制了找到的最大内切圆以及相关的轮廓，这个博主实现的算法可以用，但这个算法加在ui里面还是稍微的比较卡，在我看来这里其实是不用这么多的，这个算法还有其他的方法去实现，后面我会单独出一篇，毕竟这个是一个新的创新点。