BiMPM实战文本匹配【下】

引言

这是BiMPM实战文本匹配的第二篇文章。

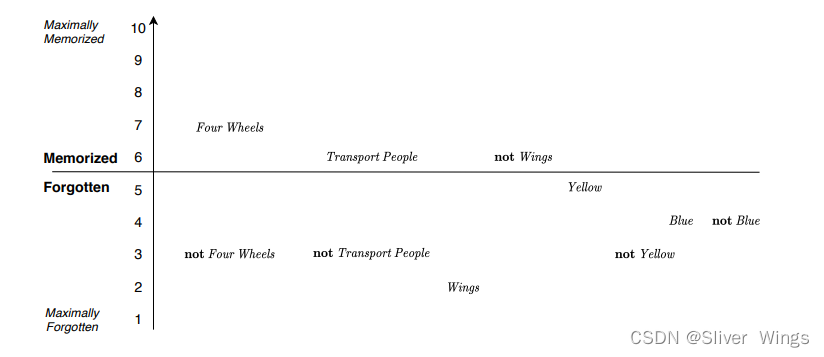
注意力匹配

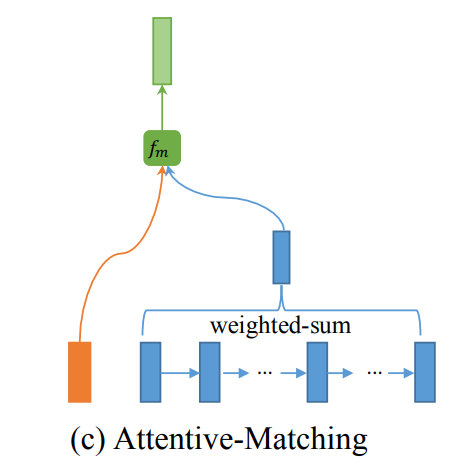
如上图所示，首先计算每个正向(或反向)上下文嵌入 $\overset{\rightarrow}{\pmb h_i^p}$ (或 $\overset{\leftarrow}{\pmb h_i^p}$ )与另一句的每个正向(或反向)上下文嵌入 $\overset{\rightarrow}{\pmb h_j^q}$ (或 $\overset{\leftarrow}{\pmb h_j^q}$ )之间的余弦相似度：

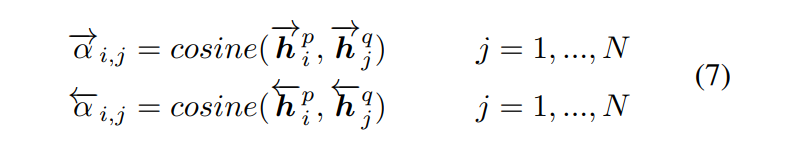
然后，把 $\overset{\rightarrow}{\alpha_{i,j}}$ (或 $\overset{\leftarrow}{\alpha_{i,j}}$ )当成 $\overset{\rightarrow}{\pmb h_j^q}$ (或 $\overset{\leftarrow}{\pmb h_j^q}$ )的权重(注意这里没有用softmax进行归一化)，接着通过加权求和句子 $Q$ 所有上下文嵌入来计算它的一个注意力向量：

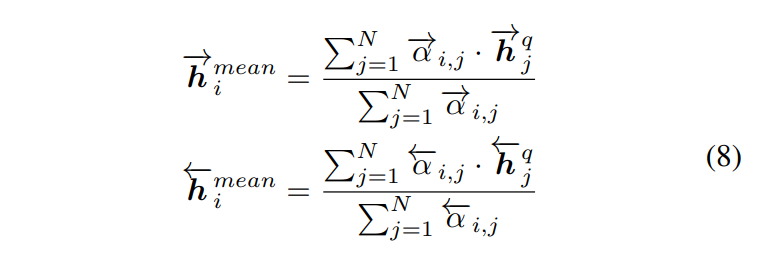
最后，为每个正向(或反向)上下文嵌入 $\overset{\rightarrow}{\pmb h_i^p}$ (或 $\overset{\leftarrow}{\pmb h_i^p}$ )和它相应的注意力向量计算匹配：

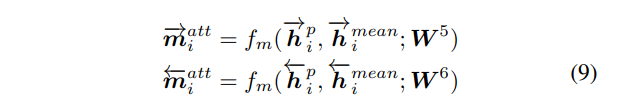
这种匹配方式又复杂了一点，但可以分步来看。

第一步，如公式 $(7)$ 所示，直接计算这两个序列之间的余弦相似度，得到第一个序列每个时间步上对应另一个序列所有时间步上的余弦相似度值，得到一个余弦相似度矩阵。

第二步，把这个余弦相似度值当成权重去对第二个序列计算加权，然后除以第二个序列所有时间步上的余弦相似度值总和；

第三步，用第一个序列的原始向量和第二步计算加权后的向量去计算匹配。

    def _attentive_matching(
        self, v1: Tensor, v2: Tensor, cosine_matrix: Tensor, w: Tensor
    ) -> Tensor:
        """

        Args:
            v1 (Tensor): (batch_size, seq_len1, hidden_size)
            v2 (Tensor): (batch_size, seq_len2, hidden_size)
            cosine_matrix (Tensor): (batch_size, seq_len1, seq_len2)
            w (Tensor):  (l, hidden_size)

        Returns:
            Tensor:
        """
		
        # (batch_size, seq_len1, hidden_size)
        attentive_vec = self._mean_attentive_vectors(v2, cosine_matrix)
        
        # (batch_size, seq_len1, num_perspective, hidden_size)
        attentive_vec = self._time_distributed_multiply(attentive_vec, w)
        # (batch_size, seq_len, num_perspective, hidden_size)
        v1 = self._time_distributed_multiply(v1, w)
        
        # (batch_size, seq_len1, num_perspective)
        return self._cosine_similarity(v1, attentive_vec)

第一步的结果作为这里的参数cosine_matrix，从它的形状(batch_size, seq_len1, seq_len2)也可以看出来。

第二步通过attentive_vec = self._mean_attentive_vectors(v2, cosine_matrix)计算。传入的是v2，表示以v1为主。

第三步就是后面的代码，分别计算加权后的向量，然后计算匹配。

我们继续来看第一步的结果是如何计算的，其实很简单：

# (batch_size, seq_len1, hidden_size) -> (batch_size, seq_len1, 1, hidden_size)
v1 = v1.unsqueeze(2)
# (batch_size, seq_len2, hidden_size) -> (batch_size, 1, seq_len2, hidden_size)
v2 = v2.unsqueeze(1)
# (batch_size, seq_len1, seq_len2)
cosine_matrix = self._cosine_similarity(v1, v2)

还是利用广播，然后在hidden_size维度上计算余弦相似度。

然后第二步的实现为：

    def _mean_attentive_vectors(self, v2: Tensor, cosine_matrix: Tensor) -> Tensor:
        """
        calculte mean attentive vector for the entire sentence by weighted summing all
        the contextual embeddings of the entire sentence.

        Args:
            v2 (Tensor):  v2 (batch_size, seq_len2, hidden_size)
            cosine_matrix (Tensor): cosine_matrix (batch_size, seq_len1, seq_len2)

        Returns:
            Tensor: (batch_size, seq_len1, hidden_size)
        """

        #  (batch_size, seq_len1, seq_len2, 1)
        expanded_cosine_matrix = cosine_matrix.unsqueeze(-1)
        # (batch_size, 1, seq_len2, hidden_size)
        v2 = v2.unsqueeze(1)
        # (batch_size, seq_len1, hidden_size)
        weighted_sum = (expanded_cosine_matrix * v2).sum(2)
        # (batch_size, seq_len1, 1)
        sum_cosine = (cosine_matrix.sum(-1) + self.epsilon).unsqueeze(-1)
        # (batch_size, seq_len1, hidden_size)
        return weighted_sum / sum_cosine

它接收第二个序列和余弦相似度矩阵。

为了让cosine_matrix当成权重，它要去乘v2，也要分别对它们进行扩充维度。

expanded_cosine_matrix会被广播为(batch_size, seq_len1, seq_len2, hidden_size)；v2.unsqueeze(1)也会被广播为(batch_size, seq_len1, seq_len2, hidden_size)。

然后就可以逐元素相乘，得到(batch_size, seq_len1, seq_len2, hidden_size)的结果，加权需要在第二个序列的时间步维度上进行求和，所以就是sum(2)，变成了(batch_size, seq_len1, hidden_size)。

此时我们仅得到公式 $(8)$ 上的分子。

接下来我们要计算分母。分母就更简单了，直接拿cosine_matrix也在第二个序列的时间步维度上求和：

sum_cosine = (cosine_matrix.sum(-1) + self.epsilon).unsqueeze(-1)，同时保持最后一个维度，相当于用了keepdim=True。同样，为了防止分母为零，还加了一个极小数。

最后用分子除以分母就得到了公式 $(8)$ 的计算结果。

回到_attentive_matching中，后面的代码实现了公式 $(9)$ 的，即分别乘以视角权重后进行匹配。

注意这里有一个相对关系，不仅需要计算 $P$ 对 $Q$ 的注意力匹配，还要计算 $Q$ 对 $P$ 的注意力匹配。

最大注意力匹配

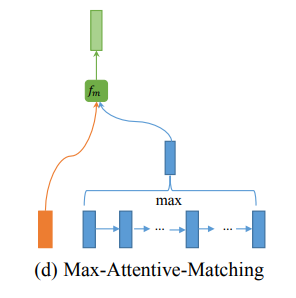
上图显示了这种匹配策略的图示。这个策略类似于注意力匹配策略。然而，与将所有上下文嵌入的加权和作为注意向量不同，这里选择与最高余弦相似度的上下文嵌入作为注意向量。然后，我们将句子 $P$ 的每个上下文嵌入与其新的注意向量进行匹配。

    def _max_attentive_matching(
        self, v1: Tensor, v2: Tensor, cosine_matrix: Tensor, w: Tensor
    ) -> Tensor:
        """

        Args:
            v1 (Tensor): (batch_size, seq_len1, hidden_size)
            v2 (Tensor): (batch_size, seq_len2, hidden_size)
            cosine_matrix (Tensor): (batch_size, seq_len1, seq_len2)
            w (Tensor): (num_perspective, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len1, num_perspective)
        """
		# (batch_size, seq_len1, embedding_szie)
        max_attentive_vec = self._max_attentive_vectors(v2, cosine_matrix)
        # (batch_size, seq_len1, num_perspective, hidden_size)
        max_attentive_vec = self._time_distributed_multiply(max_attentive_vec, w)
        # (batch_size, seq_len1, num_perspective, hidden_size)
        v1 = self._time_distributed_multiply(v1, w)
        
        # (batch_size, seq_len1, num_perspective)
        return self._cosine_similarity(v1, max_attentive_vec)

首先计算v1和v2的余弦相似度矩阵，这里和注意力匹配中一样。然后让从中选择最高余弦相似度对应的那个时间步作为待匹配的注意力向量。最后用v1和这个注意力向量去计算匹配。

这里_max_attentive_vectors实现为：

    def _max_attentive_vectors(self, v2: Tensor, cosine_matrix: Tensor) -> Tensor:
        """
        calculte max attentive vector for the entire sentence by picking
        the contextual embedding with the highest cosine similarity.

        Args:
            v2 (Tensor): v2 (batch_size, seq_len2, hidden_size)
            cosine_matrix (Tensor): cosine_matrix (batch_size, seq_len1, seq_len2)

        Returns:
            Tensor: (batch_size, seq_len1, hidden_size)
        """

        # (batch_size, seq_len1) index value between [0, seq_len2)
        _, max_v2_step_idx = cosine_matrix.max(-1)

        hidden_size = v2.size(-1)
        seq_len1 = max_v2_step_idx.size(-1)

        # (batch_size * seq_len2, hidden_size)
        v2 = v2.contiguous().view(-1, hidden_size)

        # (batch_size * seq_len1, )
        max_v2_step_idx = max_v2_step_idx.contiguous().view(-1)

        # (batch_size * seq_len1, hidden_size)
        max_v2 = v2[max_v2_step_idx]
        # (batch_size, seq_len1, hidden_size)
        return max_v2.view(-1, seq_len1, hidden_size)

余弦相似度矩阵cosine_matrix的形状为(batch_size, seq_len1, seq_len2)，要想从v2中时间步维度上取最大值，需要先从cosine_matrix获取余弦相似度最大值对应的索引，max_v2_step_idx就是这个索引，它的取值返回是[0, seq_len2)，可以包含重复值。

然后先把v2转换成 (batch_size * seq_len2, hidden_size)，索引也转换为(batch_size * seq_len1, )的形状。

通过v2[max_v2_step_idx]取得(batch_size * seq_len1, hidden_size)形状的结果。

最后转换回v1的形状。

接下来是剩下和v1去进行多视角匹配。

匹配层完整代码

class MatchingLayer(nn.Module):
    def __init__(self, args: Namespace) -> None:
        super().__init__()
        self.args = args
        self.l = args.num_perspective

        self.epsilon = args.epsilon  # prevent dividing zero

        for i in range(1, 9):
            self.register_parameter(
                f"mp_w{i}",
                nn.Parameter(torch.rand(self.l, args.hidden_size)),
            )

        self.reset_parameters()

    def reset_parameters(self):
        for _, parameter in self.named_parameters():
            nn.init.kaiming_normal_(parameter)

    def extra_repr(self) -> str:
        return ",".join([p[0] for p in self.named_parameters()])

    def forward(self, p: Tensor, q: Tensor) -> Tensor:
        """
        p: (batch_size, seq_len_p, 2 * hidden_size)
        q: (batch_size, seq_len_q, 2 * hidden_size)
        """
        # both p_fw and p_bw are (batch_size, seq_len_p, hidden_size)
        p_fw, p_bw = torch.split(p, self.args.hidden_size, -1)
        # both q_fw and q_bw are (batch_size, seq_len_q, hidden_size)
        q_fw, q_bw = torch.split(q, self.args.hidden_size, -1)

        # 1. Full Matching
        # (batch_size, seq_len1, 2 * l)
        m1 = torch.cat(
            [
                self._full_matching(p_fw, q_fw[:, -1, :], self.mp_w1),
                self._full_matching(p_bw, q_bw[:, 0, :], self.mp_w2),
            ],
            dim=-1,
        )

        # 2. Maxpooling Matching
        # (batch_size, seq_len1, 2 * l)
        m2 = torch.cat(
            [
                self._max_pooling_matching(p_fw, q_fw, self.mp_w3),
                self._max_pooling_matching(p_bw, q_bw, self.mp_w4),
            ],
            dim=-1,
        )

        # 3. Attentive Matching
        # (batch_size, seq_len1, seq_len2)
        consine_matrix_fw = self._consine_matrix(p_fw, q_fw)
        # (batch_size, seq_len1, seq_len2)
        consine_matrix_bw = self._consine_matrix(p_bw, q_bw)
        # (batch_size, seq_len1, 2 * l)
        m3 = torch.cat(
            [
                self._attentive_matching(p_fw, q_fw, consine_matrix_fw, self.mp_w5),
                self._attentive_matching(p_bw, q_bw, consine_matrix_bw, self.mp_w6),
            ],
            dim=-1,
        )

        # 4. Max Attentive Matching
        # (batch_size, seq_len1, 2 * l)
        m4 = torch.cat(
            [
                self._max_attentive_matching(p_fw, q_fw, consine_matrix_fw, self.mp_w7),
                self._max_attentive_matching(p_bw, q_bw, consine_matrix_bw, self.mp_w8),
            ],
            dim=-1,
        )

        # (batch_size, seq_len1, 8 * l)
        return torch.cat([m1, m2, m3, m4], dim=-1)

    def _cosine_similarity(self, v1: Tensor, v2: Tensor) -> Tensor:
        """compute cosine similarity between v1 and v2.

        Args:
            v1 (Tensor): (..., hidden_size)
            v2 (Tensor): (..., hidden_size)

        Returns:
            Tensor: (..., l)
        """
        # element-wise multiply
        cosine = v1 * v2
        # caculate on hidden_size dimenstaion
        cosine = cosine.sum(-1)
        # caculate on hidden_size dimenstaion
        v1_norm = torch.sqrt(torch.sum(v1**2, -1).clamp(min=self.epsilon))
        v2_norm = torch.sqrt(torch.sum(v2**2, -1).clamp(min=self.epsilon))
        # (batch_size, seq_len, l) or (batch_size, seq_len1, seq_len2, l)
        return cosine / (v1_norm * v2_norm)

    def _time_distributed_multiply(self, x: Tensor, w: Tensor) -> Tensor:
        """element-wise multiply vector and weights.

        Args:
            x (Tensor): sequence vector (batch_size, seq_len, hidden_size) or singe vector (batch_size, hidden_size)
            w (Tensor): weights (num_perspective, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len, num_perspective, hidden_size) or (batch_size, num_perspective, hidden_size)
        """

        # dimension of x
        n_dim = x.dim()
        hidden_size = x.size(-1)
        # if n_dim == 3
        seq_len = x.size(1)

        # (batch_size * seq_len, hidden_size) for n_dim == 3
        # (batch_size, hidden_size) for n_dim == 2
        x = x.contiguous().view(-1, hidden_size)

        # (batch_size * seq_len, 1, hidden_size) for n_dim == 3
        # (batch_size, 1, hidden_size) for n_dim == 2
        x = x.unsqueeze(1)

        # (1, num_perspective, hidden_size)
        w = w.unsqueeze(0)

        # (batch_size * seq_len, num_perspective, hidden_size) for n_dim == 3
        # (batch_size, num_perspective, hidden_size) for n_dim == 2
        x = x * w

        # reshape to original shape
        if n_dim == 3:
            # (batch_size, seq_len, num_perspective, hidden_size)
            x = x.view(-1, seq_len, self.l, hidden_size)
        elif n_dim == 2:
            # (batch_size, num_perspective, hidden_size)
            x = x.view(-1, self.l, hidden_size)
        # (batch_size, seq_len, num_perspective, hidden_size) for n_dim == 3
        # (batch_size, num_perspective, hidden_size) for n_dim == 2
        return x

    def _full_matching(self, v1: Tensor, v2_last: Tensor, w: Tensor) -> Tensor:
        """full matching operation.

        Args:
            v1 (Tensor): the full embedding vector sequence (batch_size, seq_len1, hidden_size)
            v2_last (Tensor): single embedding vector (batch_size, hidden_size)
            w (Tensor): weights of one direction (num_perspective, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len1, num_perspective)
        """

        # (batch_size, seq_len1, num_perspective, hidden_size)
        v1 = self._time_distributed_multiply(v1, w)
        # (batch_size, num_perspective, hidden_size)
        v2 = self._time_distributed_multiply(v2_last, w)
        # (batch_size, 1, num_perspective, hidden_size)
        v2 = v2.unsqueeze(1)
        # (batch_size, seq_len1, num_perspective)
        return self._cosine_similarity(v1, v2)

    def _max_pooling_matching(self, v1: Tensor, v2: Tensor, w: Tensor) -> Tensor:
        """max pooling matching operation.

        Args:
            v1 (Tensor): (batch_size, seq_len1, hidden_size)
            v2 (Tensor): (batch_size, seq_len2, hidden_size)
            w (Tensor): (num_perspective, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len1, num_perspective)
        """

        # (batch_size, seq_len1, num_perspective, hidden_size)
        v1 = self._time_distributed_multiply(v1, w)
        # (batch_size, seq_len2, num_perspective, hidden_size)
        v2 = self._time_distributed_multiply(v2, w)
        # (batch_size, seq_len1, 1, num_perspective, hidden_size)
        v1 = v1.unsqueeze(2)
        # (batch_size, 1, seq_len2, num_perspective, hidden_size)
        v2 = v2.unsqueeze(1)
        # (batch_size, seq_len1, seq_len2, num_perspective)
        cosine = self._cosine_similarity(v1, v2)
        # (batch_size, seq_len1, num_perspective)
        return cosine.max(2)[0]

    def _consine_matrix(self, v1: Tensor, v2: Tensor) -> Tensor:
        """
        Args:
            v1 (Tensor): (batch_size, seq_len1, hidden_size)
            v2 (Tensor): _description_

        Returns:
            Tensor: (batch_size, seq_len1, seq_len2)
        """

        # (batch_size, seq_len1, 1, hidden_size)
        v1 = v1.unsqueeze(2)
        # (batch_size, 1, seq_len2, hidden_size)
        v2 = v2.unsqueeze(1)
        # (batch_size, seq_len1, seq_len2)
        return self._cosine_similarity(v1, v2)

    def _mean_attentive_vectors(self, v2: Tensor, cosine_matrix: Tensor) -> Tensor:
        """
        calculte mean attentive vector for the entire sentence by weighted summing all
        the contextual embeddings of the entire sentence.

        Args:
            v2 (Tensor):  v2 (batch_size, seq_len2, hidden_size)
            cosine_matrix (Tensor): cosine_matrix (batch_size, seq_len1, seq_len2)

        Returns:
            Tensor: (batch_size, seq_len1, hidden_size)
        """

        #  (batch_size, seq_len1, seq_len2, 1)
        expanded_cosine_matrix = cosine_matrix.unsqueeze(-1)
        # (batch_size, 1, seq_len2, hidden_size)
        v2 = v2.unsqueeze(1)
        # (batch_size, seq_len1, hidden_size)
        weighted_sum = (expanded_cosine_matrix * v2).sum(2)
        # (batch_size, seq_len1, 1)
        sum_cosine = (cosine_matrix.sum(-1) + self.epsilon).unsqueeze(-1)
        # (batch_size, seq_len1, hidden_size)
        return weighted_sum / sum_cosine

    def _max_attentive_vectors(self, v2: Tensor, cosine_matrix: Tensor) -> Tensor:
        """
        calculte max attentive vector for the entire sentence by picking
        the contextual embedding with the highest cosine similarity.

        Args:
            v2 (Tensor): v2 (batch_size, seq_len2, hidden_size)
            cosine_matrix (Tensor): cosine_matrix (batch_size, seq_len1, seq_len2)

        Returns:
            Tensor: (batch_size, seq_len1, hidden_size)
        """

        # (batch_size, seq_len1) index value between [0, seq_len2)
        _, max_v2_step_idx = cosine_matrix.max(-1)

        hidden_size = v2.size(-1)
        seq_len1 = max_v2_step_idx.size(-1)

        # (batch_size * seq_len2, hidden_size)
        v2 = v2.contiguous().view(-1, hidden_size)

        # (batch_size * seq_len1, )
        max_v2_step_idx = max_v2_step_idx.contiguous().view(-1)

        # (batch_size * seq_len1, hidden_size)
        max_v2 = v2[max_v2_step_idx]
        # (batch_size, seq_len1, hidden_size)
        return max_v2.view(-1, seq_len1, hidden_size)

    def _attentive_matching(
        self, v1: Tensor, v2: Tensor, cosine_matrix: Tensor, w: Tensor
    ) -> Tensor:
        """

        Args:
            v1 (Tensor): (batch_size, seq_len1, hidden_size)
            v2 (Tensor): (batch_size, seq_len2, hidden_size)
            cosine_matrix (Tensor): (batch_size, seq_len1, seq_len2)
            w (Tensor):  (l, hidden_size)

        Returns:
            Tensor:
        """

        # (batch_size, seq_len1, hidden_size)
        attentive_vec = self._mean_attentive_vectors(v2, cosine_matrix)
        # (batch_size, seq_len1, num_perspective, hidden_size)
        attentive_vec = self._time_distributed_multiply(attentive_vec, w)

        # (batch_size, seq_len, num_perspective, hidden_size)
        v1 = self._time_distributed_multiply(v1, w)
        # (batch_size, seq_len1, num_perspective)
        return self._cosine_similarity(v1, attentive_vec)

    def _max_attentive_matching(
        self, v1: Tensor, v2: Tensor, cosine_matrix: Tensor, w: Tensor
    ) -> Tensor:
        """

        Args:
            v1 (Tensor): (batch_size, seq_len1, hidden_size)
            v2 (Tensor): (batch_size, seq_len2, hidden_size)
            cosine_matrix (Tensor): (batch_size, seq_len1, seq_len2)
            w (Tensor): (num_perspective, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len1, num_perspective)
        """

        # (batch_size, seq_len1, num_perspective, hidden_size)
        v1 = self._time_distributed_multiply(v1, w)
        # (batch_size, seq_len1, embedding_szie)
        max_attentive_vec = self._max_attentive_vectors(v2, cosine_matrix)
        # (batch_size, seq_len1, num_perspective, hidden_size)
        max_attentive_vec = self._time_distributed_multiply(max_attentive_vec, w)

        # (batch_size, seq_len1, num_perspective)
        return self._cosine_similarity(v1, max_attentive_vec)

第79行将所有这四种匹配策略应用于句子 $P$ 的每个时间步，并将生成的八个向量拼接在一起，作为 $P$ 的每个时间步的匹配向量。

还对反向匹配方向执行相同的过程，最终得到两个匹配向量。

聚合层

用于将上面的两个匹配向量序列聚合成一个定长匹配向量。这里使用了另一个BiLSTM层，并且单独应用在这两个匹配向量序列上，通过拼接BiLSTM最后一个时间步的向量(图1四个绿色的向量)又构建了新的定长向量。每个匹配向量序列应用到BiLSTM上会同时得到正向和负向的最后一个时间步的输出，两个匹配向量序列就可以得到四个。

class AggregationLayer(nn.Module):
    def __init__(self, args: Namespace):
        super().__init__()

        self.agg_lstm = nn.LSTM(
            input_size=args.num_perspective * 8,
            hidden_size=args.hidden_size,
            batch_first=True,
            bidirectional=True,
        )

        self.reset_parameters()

    def reset_parameters(self):
        nn.init.kaiming_normal_(self.agg_lstm.weight_ih_l0)
        nn.init.constant_(self.agg_lstm.bias_ih_l0, val=0)
        nn.init.orthogonal_(self.agg_lstm.weight_hh_l0)
        nn.init.constant_(self.agg_lstm.bias_hh_l0, val=0)

        nn.init.kaiming_normal_(self.agg_lstm.weight_ih_l0_reverse)
        nn.init.constant_(self.agg_lstm.bias_ih_l0_reverse, val=0)
        nn.init.orthogonal_(self.agg_lstm.weight_hh_l0_reverse)
        nn.init.constant_(self.agg_lstm.bias_hh_l0_reverse, val=0)

    def forward(self, v1: Tensor, v2: Tensor) -> Tensor:
        """

        Args:
            v1 (Tensor): (batch_size, seq_len1, l * 8)
            v2 (Tensor): (batch_size, seq_len2, l * 8)


        Returns:
            Tensor: (batch_size, 4 * hidden_size)
        """

        batch_size = v1.size(0)

        # v1_last (2, batch_size, hidden_size)
        _, (v1_last, _) = self.agg_lstm(v1)
        # v2_last (2, batch_size, hidden_size)
        _, (v2_last, _) = self.agg_lstm(v2)

        # v1_last (batch_size, 2, hidden_size)
        v1_last = v1_last.transpose(1, 0)
        v2_last = v2_last.transpose(1, 0)
        # v1_last (batch_size, 2 * hidden_size)
        v1_last = v1_last.contiguous().view(batch_size, -1)
        # v2_last (batch_size, 2 * hidden_size)
        v2_last = v2_last.contiguous().view(batch_size, -1)

        # (batch_size, 4 * hidden_size)
        return torch.cat([v1_last, v2_last], dim=-1)

聚合层相比较来说就非常简单了。

要注意的是这里如何取最后一个时间步的状态，最后拼接成(batch_size, 4 * hidden_size)的输出。

预测层

该层的目标是评估我们需要的概率分布 $\text{Pr}(y|P,Q)$ 。作者应用了一个两层前馈网络，输入是上一层的定长向量。

class Prediction(nn.Module):
    def __init__(self, args: Namespace) -> None:
        super().__init__()
        self.predict = nn.Sequential(
            nn.Linear(args.hidden_size * 4, args.hidden_size * 2),
            nn.ReLU(),
            nn.Dropout(args.dropout),
            nn.Linear(args.hidden_size * 2, args.num_classes),
        )

        self.reset_parameters()

    def reset_parameters(self) -> None:
        nn.init.uniform_(self.predict[0].weight, -0.005, 0.005)
        nn.init.constant_(self.predict[0].bias, val=0)

        nn.init.uniform_(self.predict[-1].weight, -0.005, 0.005)
        nn.init.constant_(self.predict[-1].bias, val=0)

    def forward(self, x: Tensor) -> Tensor:
        return self.predict(x)

和前几个模型的实现类似，这里是一个双层FFN。

最后的最后把这些网络层组合到一起，构成BiMPM的实现。

BiMPM实现

class BiMPM(nn.Module):
    def __init__(self, args: Namespace) -> None:
        super().__init__()
        self.args = args
        # the concatenated embedding size of word
        self.d = args.word_embedding_dim + args.char_hidden_size
        self.l = args.num_perspective

        self.word_rep = WordRepresentation(args)
        self.context_rep = ContextRepresentation(args)
        self.matching_layer = MatchingLayer(args)
        self.aggregation = AggregationLayer(args)
        self.prediction = Prediction(args)

    def dropout(self, x: Tensor) -> Tensor:
        return F.dropout(input=x, p=self.args.dropout, training=self.training)

    def forward(self, p: Tensor, q: Tensor, char_p: Tensor, char_q: Tensor) -> Tensor:
        """

        Args:
            p (Tensor): word inpute sequence (batch_size, seq_len1)
            q (Tensor): word inpute sequence (batch_size, seq_len2)
            char_p (Tensor): character input sequence (batch_size, seq_len1, word_len)
            char_q (Tensor): character input sequence (batch_size, seq_len1, word_len)

        Returns:
            Tensor: (batch_size,  2)
        """

        # (batch_size, seq_len1, word_embedding_dim + char_hidden_size)
        p_rep = self.dropout(self.word_rep(p, char_p))
        # (batch_size, seq_len2, word_embedding_dim + char_hidden_size)
        q_rep = self.dropout(self.word_rep(q, char_q))
        #  batch_size, seq_len1, 2 * hidden_size)
        p_context = self.dropout(self.context_rep(p_rep))
        #  batch_size, seq_len2, 2 * hidden_size)
        q_context = self.dropout(self.context_rep(q_rep))
        # (batch_size, seq_len1, 8 * l)
        p_match = self.dropout(self.matching_layer(p_context, q_context))
        # (batch_size, seq_len2, 8 * l)
        q_match = self.dropout(self.matching_layer(q_context, p_context))

        # (batch_size,  4 * hidden_size)
        aggregation = self.dropout(self.aggregation(p_match, q_match))
        # (batch_size,  2)
        return self.prediction(aggregation)

模型训练

定义指标函数：

def metrics(y: torch.Tensor, y_pred: torch.Tensor) -> Tuple[float, float, float, float]:
    TP = ((y_pred == 1) & (y == 1)).sum().float()  # True Positive
    TN = ((y_pred == 0) & (y == 0)).sum().float()  # True Negative
    FN = ((y_pred == 0) & (y == 1)).sum().float()  # False Negatvie
    FP = ((y_pred == 1) & (y == 0)).sum().float()  # False Positive
    p = TP / (TP + FP).clamp(min=1e-8)  # Precision
    r = TP / (TP + FN).clamp(min=1e-8)  # Recall
    F1 = 2 * r * p / (r + p).clamp(min=1e-8)  # F1 score
    acc = (TP + TN) / (TP + TN + FP + FN).clamp(min=1e-8)  # Accurary
    return acc, p, r, F1

定义评估和训练函数：

def evaluate(
    data_iter: DataLoader, model: nn.Module
) -> Tuple[float, float, float, float]:
    y_list, y_pred_list = [], []
    model.eval()
    for x1, x2, c1, c2, y in tqdm(data_iter):
        x1 = x1.to(device).long()
        x2 = x2.to(device).long()
        c1 = c1.to(device).long()
        c2 = c2.to(device).long()
        y = torch.LongTensor(y).to(device)

        output = model(x1, x2, c1, c2)

        pred = torch.argmax(output, dim=1).long()

        y_pred_list.append(pred)
        y_list.append(y)

    y_pred = torch.cat(y_pred_list, 0)
    y = torch.cat(y_list, 0)
    acc, p, r, f1 = metrics(y, y_pred)
    return acc, p, r, f1


def train(
    data_iter: DataLoader,
    model: nn.Module,
    criterion: nn.CrossEntropyLoss,
    optimizer: torch.optim.Optimizer,
    print_every: int = 500,
    verbose=True,
) -> None:
    model.train()

    for step, (x1, x2, c1, c2, y) in enumerate(tqdm(data_iter)):
        x1 = x1.to(device).long()
        x2 = x2.to(device).long()
        c1 = c1.to(device).long()
        c2 = c2.to(device).long()
        y = torch.LongTensor(y).to(device)

        output = model(x1, x2, c1, c2)

        loss = criterion(output, y)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if verbose and (step + 1) % print_every == 0:
            pred = torch.argmax(output, dim=1).long()
            acc, p, r, f1 = metrics(y, pred)

            print(
                f" TRAIN iter={step+1} loss={loss.item():.6f} accuracy={acc:.3f} precision={p:.3f} recal={r:.3f} f1 score={f1:.4f}"
            )

注意此时输入有4个。

开始训练：

		make_dirs(args.save_dir)

    if args.cuda:
        device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
    else:
        device = torch.device("cpu")

    print(f"Using device: {device}.")

    vectorizer_path = os.path.join(args.save_dir, args.vectorizer_file)

    train_df = build_dataframe_from_csv(args.dataset_csv.format("train"))
    test_df = build_dataframe_from_csv(args.dataset_csv.format("test"))
    dev_df = build_dataframe_from_csv(args.dataset_csv.format("dev"))

    print("Creating a new Vectorizer.")

    train_chars = train_df.sentence1.to_list() + train_df.sentence2.to_list()

    char_vocab = Vocabulary.build(train_chars, args.min_char_freq)

    args.char_vocab_size = len(char_vocab)

    train_word_df = tokenize_df(train_df)
    test_word_df = tokenize_df(test_df)
    dev_word_df = tokenize_df(dev_df)

    train_sentences = train_df.sentence1.to_list() + train_df.sentence2.to_list()

    word_vocab = Vocabulary.build(train_sentences, args.min_word_freq)

    args.word_vocab_size = len(word_vocab)

    words = [word_vocab.lookup_token(idx) for idx in range(args.word_vocab_size)]

    longest_word = ""

    for word in words:
        if len(word) > len(longest_word):
            longest_word = word

    args.max_word_len = len(longest_word)

    char_vectorizer = TMVectorizer(char_vocab, len(longest_word))
    word_vectorizer = TMVectorizer(word_vocab, args.max_len)

    train_dataset = TMDataset(train_df, char_vectorizer, word_vectorizer)
    test_dataset = TMDataset(test_df, char_vectorizer, word_vectorizer)
    dev_dataset = TMDataset(dev_df, char_vectorizer, word_vectorizer)

    train_data_loader = DataLoader(
        train_dataset, batch_size=args.batch_size, shuffle=True
    )
    dev_data_loader = DataLoader(dev_dataset, batch_size=args.batch_size)
    test_data_loader = DataLoader(test_dataset, batch_size=args.batch_size)

    print(f"Arguments : {args}")
    model = BiMPM(args)

    print(f"Model: {model}")

    model = model.to(device)

    optimizer = torch.optim.Adam(model.parameters(), lr=args.learning_rate)
    criterion = nn.CrossEntropyLoss()

    for epoch in range(args.num_epochs):
        train(
            train_data_loader,
            model,
            criterion,
            optimizer,
            print_every=args.print_every,
            verbose=args.verbose,
        )
        print("Begin evalute on dev set.")
        with torch.no_grad():
            acc, p, r, f1 = evaluate(dev_data_loader, model)

            print(
                f"EVALUATE [{epoch+1}/{args.num_epochs}]  accuracy={acc:.3f} precision={p:.3f} recal={r:.3f} f1 score={f1:.4f}"
            )

    model.eval()

    acc, p, r, f1 = evaluate(test_data_loader, model)
    print(f"TEST accuracy={acc:.3f} precision={p:.3f} recal={r:.3f} f1 score={f1:.4f}")

BiMPM(
  (word_rep): WordRepresentation(
    (char_embed): Embedding(4699, 20, padding_idx=0)
    (word_embed): Embedding(35092, 300)
    (char_lstm): LSTM(20, 50, batch_first=True)
  )
  (context_rep): ContextRepresentation(
    (context_lstm): LSTM(350, 100, batch_first=True, bidirectional=True)
  )
  (matching_layer): MatchingLayer(mp_w1,mp_w2,mp_w3,mp_w4,mp_w5,mp_w6,mp_w7,mp_w8)
  (aggregation): AggregationLayer(
    (agg_lstm): LSTM(160, 100, batch_first=True, bidirectional=True)
  )
  (prediction): Prediction(
    (predict): Sequential(
      (0): Linear(in_features=400, out_features=200, bias=True)
      (1): ReLU()
      (2): Dropout(p=0.1, inplace=False)
      (3): Linear(in_features=200, out_features=2, bias=True)
    )
  )
)
...
 TRAIN iter=1000 loss=0.042604 accuracy=0.984 precision=0.974 recal=1.000 f1 score=0.9868
 80%|████████  | 1500/1866 [11:37<02:49,  2.16it/s]
 TRAIN iter=1500 loss=0.057931 accuracy=0.969 precision=0.973 recal=0.973 f1 score=0.9730
100%|██████████| 1866/1866 [14:26<00:00,  2.15it/s]
Begin evalute on dev set.
100%|██████████| 69/69 [00:11<00:00,  6.12it/s]
EVALUATE [10/10]  accuracy=0.836 precision=0.815 recal=0.870 f1 score=0.8418
100%|██████████| 98/98 [00:16<00:00,  6.11it/s]
TEST accuracy=0.825 precision=0.766 recal=0.936 f1 score=0.8424
100%|██████████| 98/98 [00:16<00:00,  6.11it/s]
TEST[best f1] accuracy=0.825 precision=0.766 recal=0.936 f1 score=0.8424

测试集上的结果比ESIM好了近1个点，但模型复杂度太高了。