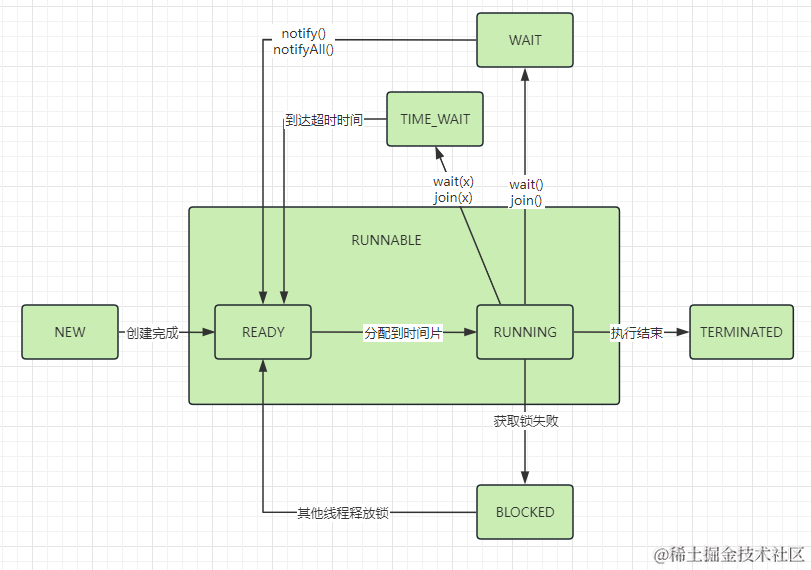
在屏幕坐标上有一个多边形，给定一个点，判断该点和多边形的关系。
例如在下图中，点A位于多边形内，点B位于多边形外，点C位于多边形上。

注意:
1.屏幕坐标系中，x轴从左往右为正方向，y轴从上到下为正方向，如示例中的坐标轴:
输入：
第一行为多边形数据，第一个数为整数，表示顶点个数，之后是顶点坐标，依次为各个点的x、y坐标的浮点数值。
例如 3 3.7 5 2 4 2.5 1.5 ，则表示有三个点组成的三角形。第二行表示待判断的点坐标，例如1.5 8.3

输出：
如果点在多边形内部，则返回0，如果在多边形上则返回1，如果在多边形外面则返回2

代码：

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
struct Point{
    double x;
    double y;
};
bool PointInPolygon2D(Point p, vector<Point>& Polygon){//判断点与多边形的关系
    int nPointNumber = Polygon.size();
    if (nPointNumber == 0)
        return false;
    int nSideNumber = nPointNumber;
    if (Polygon[0].x == Polygon[nPointNumber - 1].x && Polygon[0].y == Polygon[nPointNumber - 1].y)
        nSideNumber--;
    double epsilon = 0.000001;
    int nCross = 0;
    for (int i = 0; i < nSideNumber; i++){
        Point p1 = Polygon[i];
        Point p2 = Polygon[(i + 1) % nSideNumber];
        if (p1.y == p2.y)
            continue;
        if (p.y < min(p1.y, p2.y) || p.y >= max(p1.y, p2.y))
            continue; 
        double x = (double)(p.y - p1.y) * (double)(p2.x - p1.x) / (double)(p2.y - p1.y) + p1.x;
        if ((x - p.x) >= epsilon)
            nCross++;
    }
    if ((nCross % 2) == 1)
        return true;
    else
        return false;
}
bool isEqual(double a, double b) {//判断两个double是否相等
    return std::fabs(a - b) < 1e-6;
}
bool isPointOnSegment(Point A, Point B, Point C) {//判断点是否在线段上
    if ((C.x >= min(A.x, B.x) && C.x <= max(A.x, B.x)) &&(C.y >= min(A.y, B.y) && C.y <= max(A.y, B.y))) {
        double crossProduct = (B.y - A.y) * (C.x - A.x) - (B.x - A.x) * (C.y - A.y);
        if (isEqual(crossProduct, 0.0)) {
            return true;
        }
    }
    return false;
}
int main(){
    int n;
    double x, y;
    cin >> n;
    vector<Point> p(n);
    for(int i =0;i<n;i++){
        cin >> x >> y;
        p[i].x = x;
        p[i].y = y;
    }
    struct Point target;

    cin >> target.x >> target.y;
    for (int i = 0; i < n - 1;i++){
        if(isPointOnSegment(p[i],p[i+1],target)){
            cout << "1" << endl;
            return 0;
        }
    }
    if (PointInPolygon2D(target, p)){
        cout << "0" << endl;
        return 0;
    }
    else{
        cout << "2" << endl;
        return 0;
    }
    return 0;
}